Régression logistique

Le modèle de régression logistique est également l’un des modèles les plus populaires en machine learning pour réaliser un classement ( prédire les valeurs d'une variable qualitative sur base de prédicteurs ). Il s'agit d'une technique paramétrique - le modèle doit trouver les meilleurs paramètres au regard des données -.

Cette technique est utilisée pour ajuster la relation entre une variable qualitative $Y$ ( variable dépendante ) et un ensemble de prédicteurs $x_1, x_2,...x_n$ - variables indépendantes - qui doivent être des variables quantitatives ou des variables qualitatives transformées en variables quantitatives ( encodage one-hot ou numérisation de variables discrètes ).

Le fonctionnement de la régression logistique est quasi identique à la régression linéaire si ce n'est qu'elle utilise une fonction sigmoïde. Tout comme la régression linéaire, nous partons du postulat que $x$ et $y$ sont dépendants, c’est-à-dire que la connaissance des valeurs des $x$ permet d’améliorer la connaissance des valeurs de $y$. Il existe donc une corrélation entre $x$ et $y$ - pour rappel : au plus une variable $x$ est corrélée ( de manière positive ou négative ) à la variable $y$, au plus elle est importante pour notre modèle car on dit qu'elle est « discriminante ». - voir ( corrélation ).

La régression logistique ne prédit pas une valeur qualitative directement mais une probabilité qu'un nouvel enregistrement appartient à une classe.

remarque

Certains schémas et concepts présentés ici sont inspirés du cours Machine Learning d'Andrew Ng, programme créé en collaboration entre Stanford university Online Education et DeepLearning.AI disponible sur Coursera. Retrouvez le cours original ici : Machine Learning by Andrew Ng.

Linéaire vs logistique

Lorsque l'on évoque le concept de régression, il s'agit de tout processus qui tend à trouver des relations entre les variables.

La régression linéaire cherche à établir une relation linéaire entre la variable dépendante (y) et les variables explicatives ou indépendantes $x$ ( $x_1, x_2, x_3, ..., x_n$) ( prédicteurs ) Exemple d'une régression linéaire simple : si l’âge de la voiture est de +1, le prix sera impacté de $z$ ( selon le coefficient et l’origine de la droite ).

La régression logistique cherche également à établir une relation entre la variable dépendante ( y ) et les variables explicatives ou indépendantes $x$ ( $x_1, x_2, x_3, ..., x_n$) ( prédicteurs ) **mais utilise une fonction logistique ( le logit ) pour obtenir une valeur entre $0$ et $1$ soit une probabilité qu'un nouvel enregistrement appartienne à une classe.si l’âge de la voiture augmente de 1 an, la probabilité qu'elle tombe en panne augmentera ou diminuera en fonction du coefficient associé à l'âge dans le modèle..

L'une utilise donc une fonction linéaire alors que l'autre utilise la fonction sigmoïde qui, par une fonction linéaire sous-jacente permet de modéliser une probabilité.

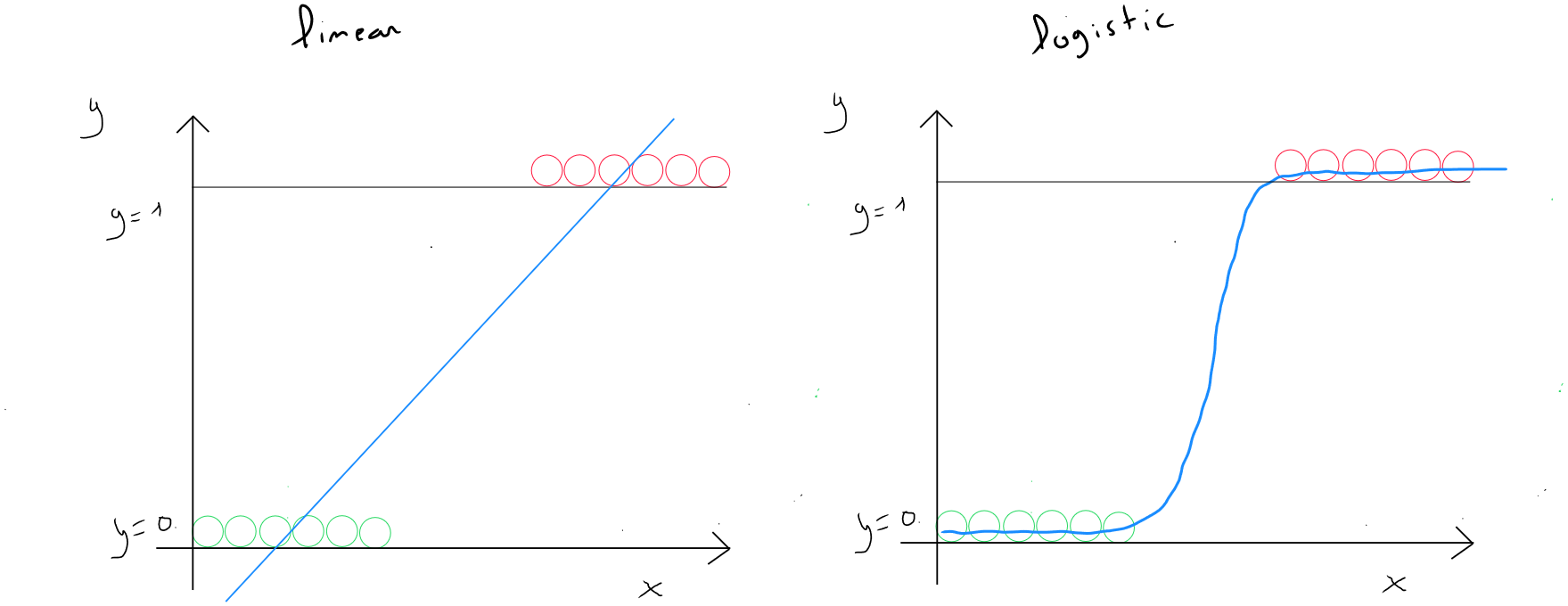
Pourquoi ne pas utiliser une régression linéaire ?

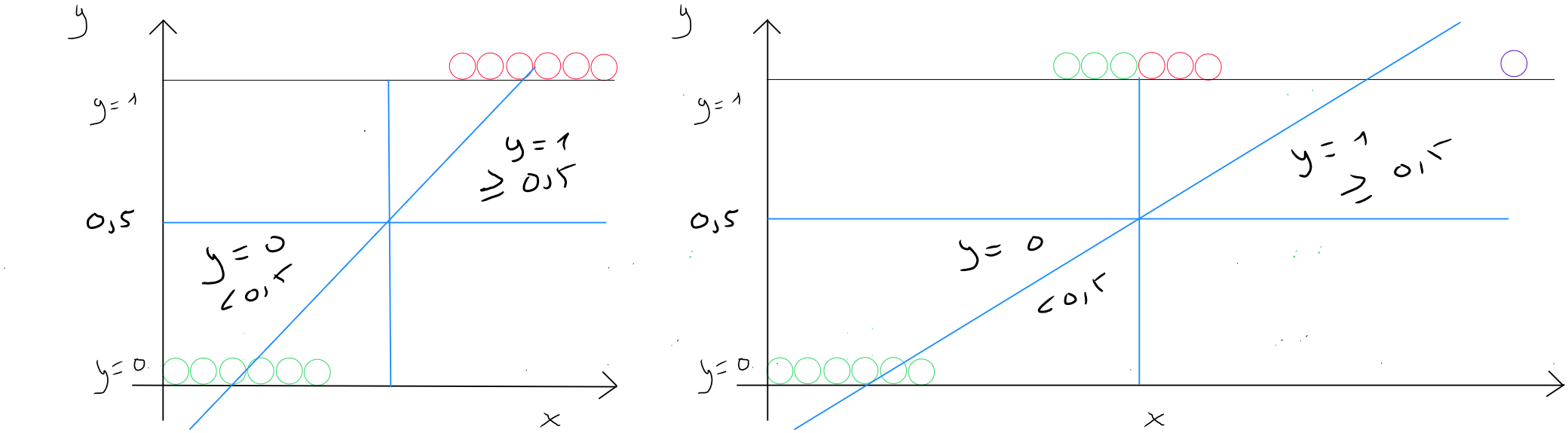
Prenons l'exemple d'un classement à deux valeurs soit $y = 1$ ou $y = 0$. J'ai donc une distribution de valeurs pour les deux cas. Si j'utilise une régression linéaire et que je trace la droite. Je pourrais, dans l'exemple illustré ci-dessous à gauche, considérer que la régression linéaire fait un travail correct en partant du postulat que nous définissons un seuil de 0,5 pour dire que toute valeur étant égale ou supérieure à $0,5$ est égale à $1$ ( la classe 1 ) et toute valeur inférieure à $0,5$ est égale à $0$ ( la classe $0$ ). Nous constatons dans le graphique de gauche que toutes les valeurs situées à droite de la perpendiculaire à $x$ ont un seuil supérieur ou égal à $0,5$ et donc $1$.

Si tout d'un coup, nous disposons d'un enregistrement dont la valeur de $x$ est bien plus importante ( graphique de droite - point mauve ), dans ce cas, la pente de la droite est modifiée et nous constatons que le modèle prédirait une partie des valeurs supérieures ou égales au seuil de $0,5$ comme faisant partie de la classe $0$.

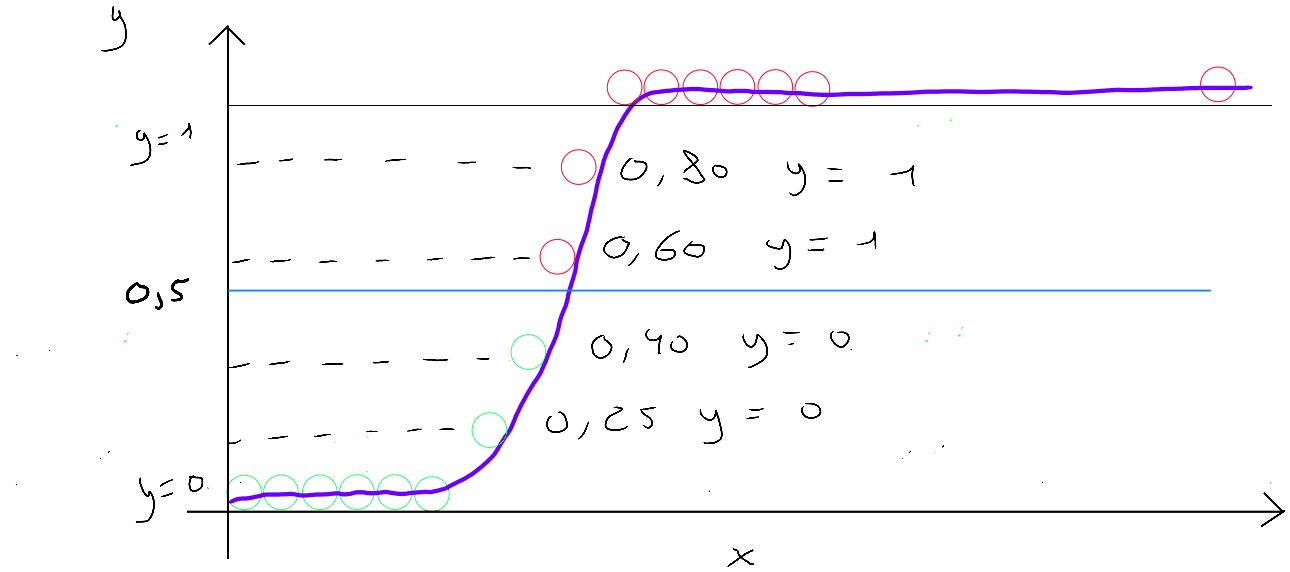
Nous devons donc utiliser une fonction qui nous permet d'obtenir une courbe dont la particularité serait d'appliquer une forme linéaire dans une sous-fonction, lors de l'augmentation exponentielle des valeurs, mais qui à son commencement et à sa fin serait plate de sorte que les valeurs resteraient toujours comprises entre $0$ et $1$. Concrètement, il s'agit d'une fonction en forme de S pour assurer que les valeurs possibles soient comprises entre $0$ et $1$.

$$\begin{aligned} \text{Si } f_{w,b}(x) &\geq 0.5 \rightarrow \hat{y} = 1\\ \text{Si } f_{w,b}(x) &< 0.5 \rightarrow \hat{y} = 0 \end{aligned}$$

Fonction sigmoïde

La fonction sigmoïde - fonction logistique - est une fonction mathématique en forme de S dont la particularité est de transformer n'importe quelle valeur en un nombre compris entre $0$ et $1$.

$$f(z) = \frac{1}{1 + e^{(-z)}}$$

ou

$$z = \vec{w} \cdot \vec{x} + b$$

$Z$ représente la sous-fonction linéaire. Tout comme la régression linéaire, l'algorithme de la régression logistique dispose de données d'entrainement, c'est à dire des $x$ et des $y$ et, sur base de ces informations, doit identifier les paramètres $w,b$ grâce à une fonction coût et l'algorithme du gradient descent pour trouver l'optimal local. Lorsque les paramètres sont identifiés, le modèle sigmoïde renvoie en sortie une valeur entre 0 et 1 - une probabilité - qui est transformée en classe sur base de la définition d'un seuil ( majoritairement $0,5$ ).

Réécrite en détail, la formule de $z$ nous donne ceci :

$$Z = b + w_1 x_1^{(i)} + w_2 x_2^{(i)} + w_3 x_3^{(i)} + ... + w_p x_p^{(i)}$$

et donc la formule de la fonction sigmoïde :

$$f(z) = \frac{1}{1 + e^{(-z)}} = \frac{1}{1 + e^{(-(b + w_1 x_1^{(i)} + w_2 x_2^{(i)} + w_3 x_3^{(i)} + ... + w_p x_p^{(i)}))}}$$

ou

$$f(z) = \frac{1}{1 + e^{(-z)}} = \frac{1}{1 + e^{(-(\vec{w} \cdot \vec{x} + b))}}$$

Si nous décortiquons la formule :

• $f(z)$ est la sortie de la fonction sigmoïde qui nous permet d'obtenir une valeur entre $0$ et $1$ ;
• $z$ est l'entrée de la fonction - qui contient les paramètres identifiés par l'algorithme du gradient descent sur base des données d'entrainement. $z$ requiert également de nouvelles valeurs de $x$ pour pouvoir prédire une probabilité ;
• $e$ est la constance d'Euler ( valeur approximative de $2,71828$ ) et joue un rôle crucial dans l'obtention de la forme en S ;

attention

Peu importe la valeur de $Z$, l’exposant négatif de la constante d'Euler au dénominateur fera en sorte que :

• si $Z$ est une très grande valeur positive $( +∞ )$, la fonction sigmoïde ramènera à un maximum de $1$ ;
• si $Z$ est une très grande valeur négative $( -∞ )$, la fonction sigmoïde ramènera à un maximum de $0$ ;

Fonction sigmoïde en python

def sigmoid(z):
    g = 1/(1+np.exp(-z))
    return g

# (z = np.dot(X[i],w)+b) - define later in the cost function

Seuil de décision

La régression logistique nous permet d'obtenir en sortie de la fonction $f$, une valeur comprise entre $0$ et $1$ et nous devons, en tant que data scientist, définir le seuil de la classe $1$ ou la classe $0$. Dans la littérature, le seuil de $0,5$ est souvent mentionné de tel sorte que si la valeur de prédiction est $>= 0,5$ alors $\hat{y} = 1$ et si la valeur de prédiction est $< 0,5$ alors $\hat{y} = 0$.

Seuil linéaire

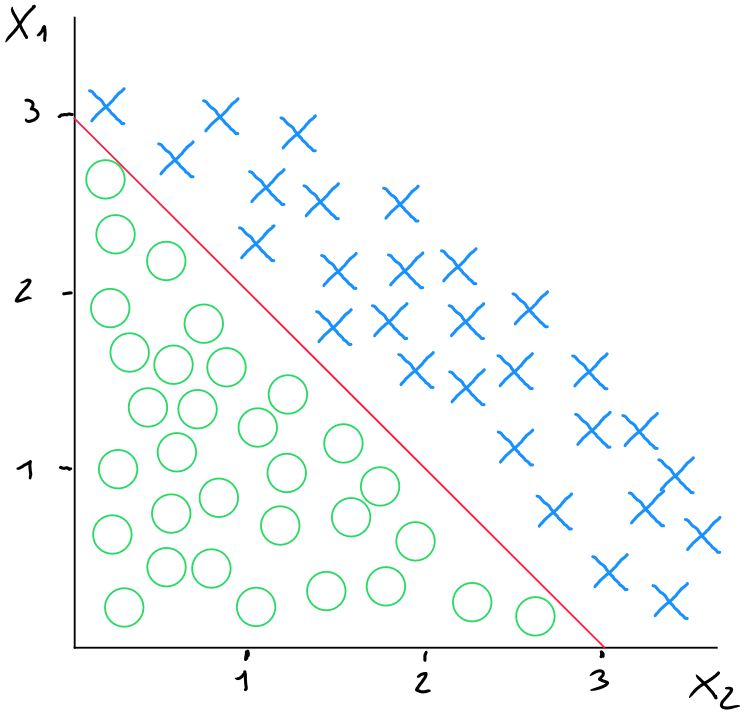
Dans le cas d'une décision de type linéaire sur la base de deux prédicteurs ( $x_1, X_2$ ), nous pourrions représenter les données comme suit (schéma ci-dessous) pour les valeurs où $z = \vec{w} \cdot \vec{x} + b$, ce qui correspond à $z = w_1 \cdot x_1 + w_2 \cdot x_2 + b$

Pour simplifier l'exemple, prenons 1 comme valeur pour $w_1$ et $w_2$, et - 3 pour $b$.

Le seuil de décision linéaire correspondrait dans ce cas-ci au moment où $z = \vec{w} \cdot \vec{x} + b = 0$ ; car ce seuil serait neutre pour définir si $y = 1$ (croix rouge) ou $y = 0$ (rond bleu).

Dans notre cas, étant donné que $w_1$ et $w_2$ valent 1 et que $b$ vaut -3, nous pouvons réécrire la formule comme suit : $z = x_1 + x_2 - 3 = 0$ ; Ainsi, $x_1 + x_2 = 3$.

La formule du seuil de décision linéaire correspond à la formule initiale de la régression logistique :

$$f(z) = \frac{1}{1 + e^{(-z)}}$$

ou

$$z = \vec{w} \cdot \vec{x} + b$$

Seuil non-linéaire

Comme nous l'avons abordé pour la régression polynomiale dans le cadre du chapitre sur la régression linéaire, nous pourrions nous retrouver dans des cas de figure de la régression logistique où la séparation des données est non-linéaire.

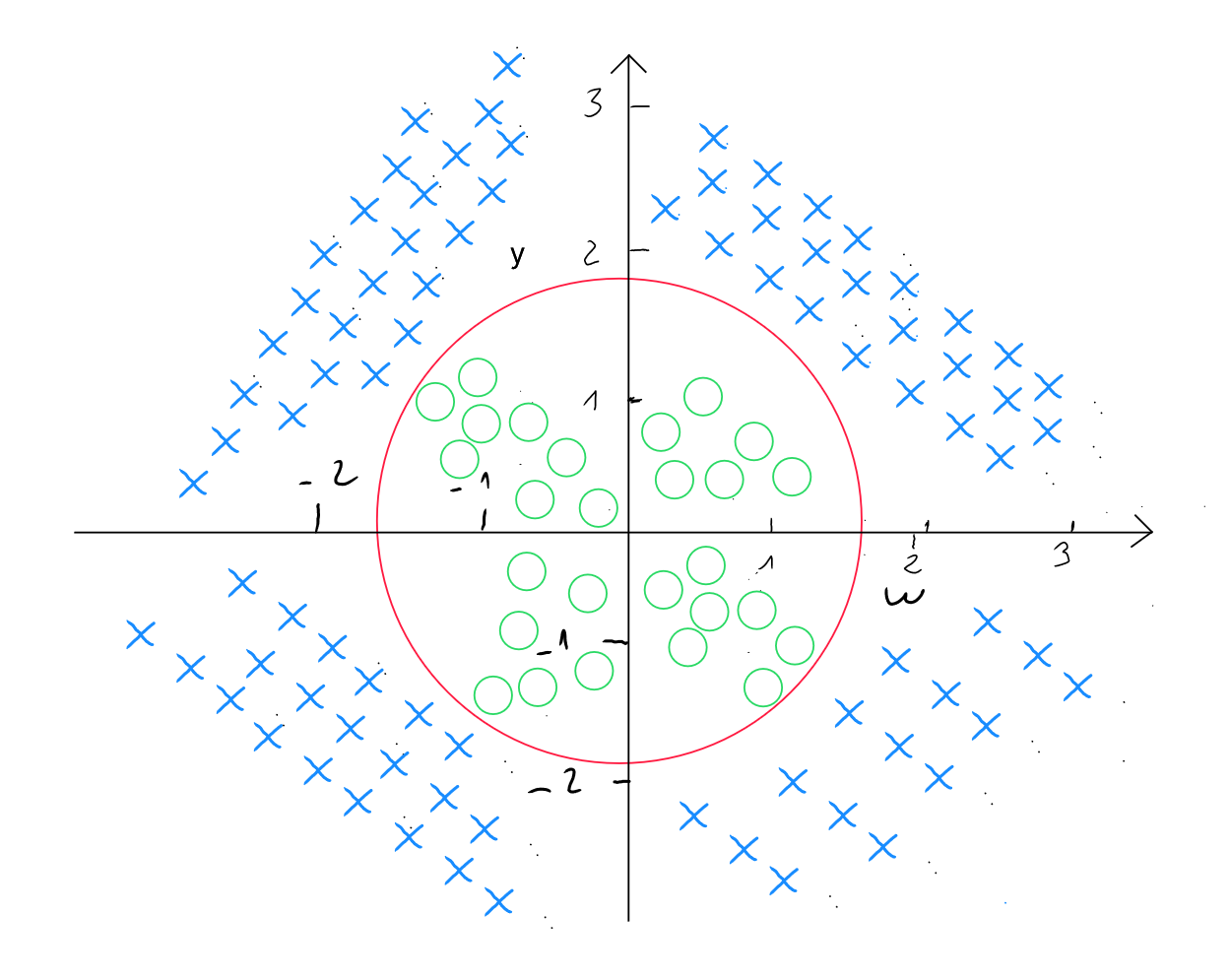
Dans le cadre d'un seuil-non linéaire, nous allons utiliser des caractéristiques polynomiales en adaptant la formule comme suit (pour deux prédicteurs $x_1$ et $x_2$) :

$$z = w_1*x_1 + w_2*x_2 + w_3*x_1^2 + w_4*x_1*x_2 + w_5*x_2^2 + .... + b$$

soit

$$f(z) = \frac{1}{1 + e^{(-(w_1*x_1 + w_2*x_2 + w_3*x_1^2 + w_4*x_1*x_2 + w_5*x_2^2 + b ))}}$$

D'autres degrés de forme polynomiale sont testés bien entendu dans le cadre de l'algorithme pour pouvoir trouver la meilleure manière de prédire l'information. Par exemple dans les cas suivants :

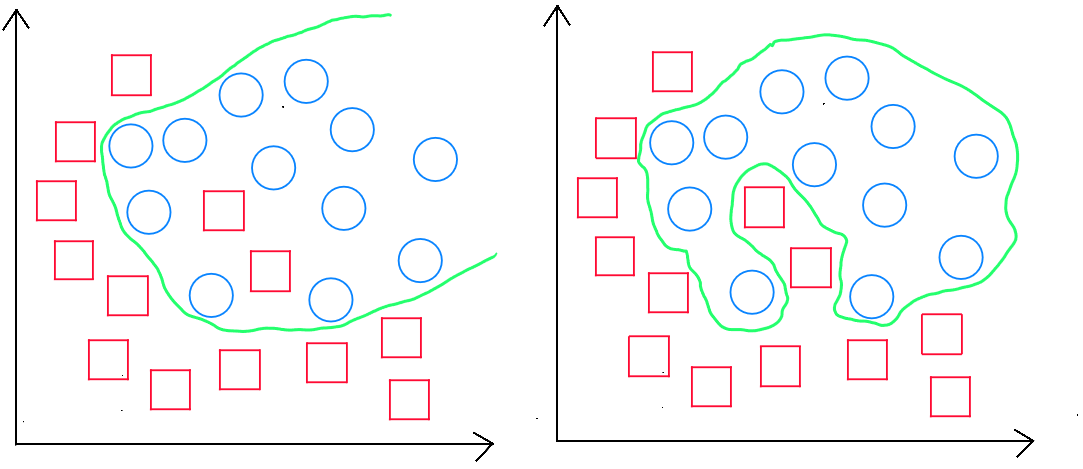
L'équation prendrait la forme suivante :

$$z = w_1*x_1 + w_2*x_2 + w_3*x_1^2 + w_4*x_1*x_2 + w_5*x_2^2 + w_6*x_1^3 + .... + b$$

Fonction polynomiale en python (Seuil non-linéaire)

import numpy as np
import pandas as pd
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.model_selection import train_test_split
import math, copy
from sklearn.metrics import confusion_matrix

# Chargement des données
data = pd.read_csv('data.csv')

# Séparation des caractéristiques et de la cible
x = data[['x_1', 'x_2', 'x_3', 'x_4', 'x_5', '...', 'x_n']].values  
y = data['y'].values  

# Génération des termes polynomiaux de degré 3
poly = PolynomialFeatures(degree=3)
x_poly = poly.fit_transform(x)

# Standardisation des données polynomiales
scaler_x = StandardScaler()
x_poly = scaler_x.fit_transform(x_poly)

# Division en ensemble d'entraînement et de test
x_train, x_test, y_train, y_test = train_test_split(x_poly, y, test_size=0.4, random_state=42)

Fonction coût

La forme de la fonction coût d'une régression linéaire est de forme convexe, ce qui est optimal pour l'algorithme du gradient descent dont l'objectif est - par itération - de trouver l'optimal pour les valeurs $w$ et $b$.

Dans une régression linéaire, nous retrouvons donc la formule suivante pour la fonction coût : $J(\vec{w}, b) = \min \left( \frac{1}{2m} \sum_{i=1}^n \left( (\vec{w} \cdot \vec{x}^{(i)} + b) - y^{(i)} \right)^2 \right)$

Le problème de la régression logistique, c'est que la forme de sa fonction coût est non convexe et par conséquent, le gradient descent peut trouver plusieurs optimal local qui ne correspondraient pas forcément à $min J(w,b)$ et serait bloqué dans sa convergence.

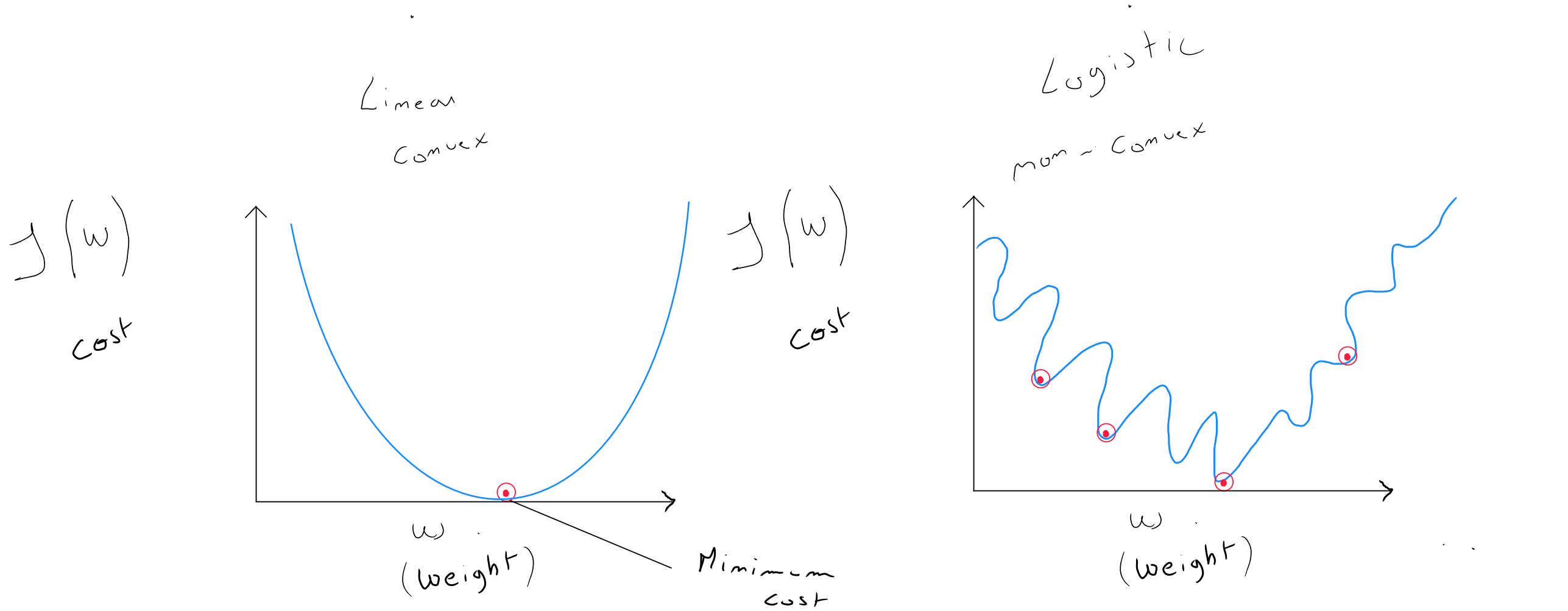
La régression logistique utilise une fonction de coût différente « transformée » de la régression linéaire afin de rendre la forme de la fonction coût convexe à nouveau et permettre de converger vers l'optimal local.

Fonction de perte

Pour adapter la fonction coût à la régression logistique, concentrons-nous sur la notion de perte qui peut s'identifier de manière isolée à la fonction coût $J(\vec{w}, b)$, en bleu dans la formule ci-dessous.

$$J(\vec{w}, b) = \min \left( \frac{1}{2m} \sum_{i=1}^n \textcolor{blue}{((\vec{w} \cdot \vec{x}^{(i)} + b) - y^{(i)})^2} \right)$$

Cette fonction perte (loss) pour tous les enregistrements, peut être réécrite comme suit :

$$\textcolor{blue}{ L(f(\vec{w},b)\vec{x}^{(i)} - y^{(i)})^2}$$
$$L(f(\vec{w},b)\vec{x}^{(i)},y^{(i)}) = \begin{cases} -log(f(\vec{w},b)\vec{x}^{(i)}) & \text{si } y^{(i)} = 1 \\ -log(1 - f(\vec{w},b)\vec{x}^{(i)}) & \text{si } y^{(i)} = 0 \end{cases}$$

Si nous visualisons $log(f)$ en considérant $f$ en abscisse (x), - sachant que $f$ est le résultat de la régression logistique ( valeur entre $0$ et $1$ ) -, cela ressemblerait à la courbe verte du schéma ci-dessous ; Et si nous visualisons $-log(f)$, nous obtiendrions la courbe bleu.

L'intersection entre les deux courbes sur l'axe des abscisse correspond à la valeur $1$. La partie de la fonction qui porte l'intérêt du résultat entre $0$ et $1$ est la partie supérieure gauche, encadrée en rouge.

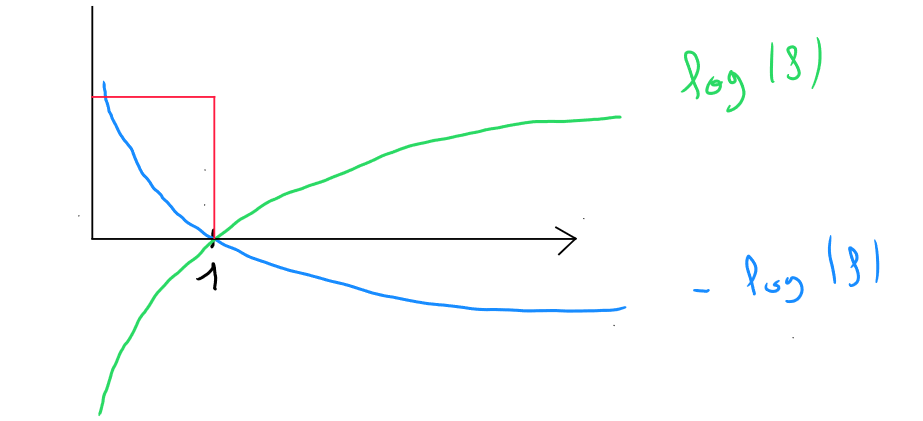
Si nous visualisons cette partie en plan serré, et que nous partons du postulat que $y =1$ ; pour la fonction de perte $L(f(\vec{w},b)\vec{x}^{(i)} - y^{(i)})^2$ et que notre modèle prédit :

• Si le modèle prédit $1$ alors la perte est de $0$
• Si le modèle prédit $0,5$ alors la perte est de $0,5$
• Si le modèle prédit $0,2$ alors la perte est de $0,8$

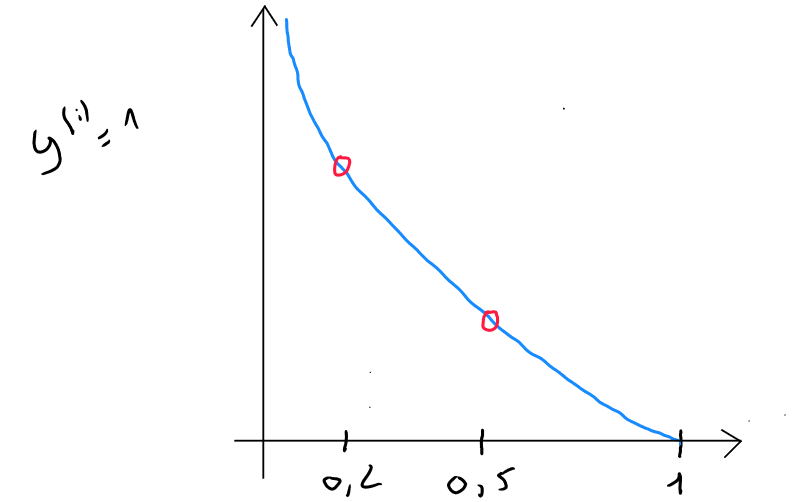
Ce que nous remarquons c'est que l'algorithme va tendre à réduire la perte et donc être le plus précis possible car les prédictions $\hat{y} = 0$ alors que $y = 1$ vont créer une perte importante.

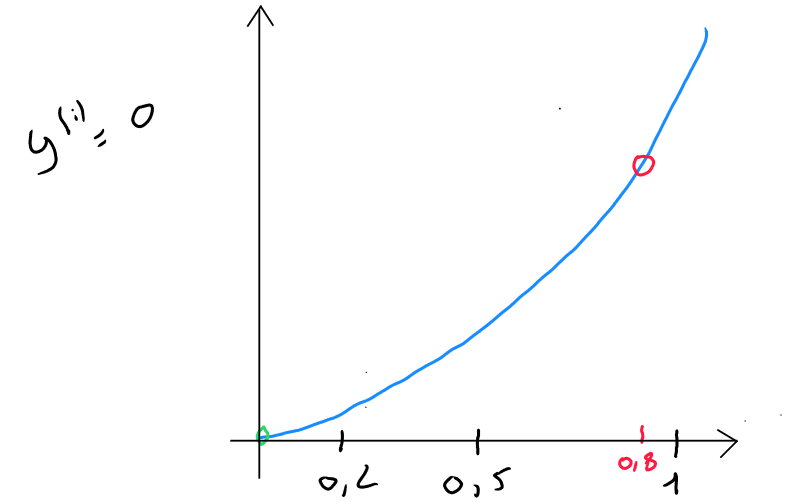
Dans le second cas ( $y =0$ ), l'algorithme va également tendre à réduire la perte et les prédictions $\hat{y} = 1$ alors que $y = 0$ vont créer une perte importante.

Par conséquent, la transformation de la fonction de coût :

$$\textcolor{blue}{ L(f(\vec{w},b)\vec{x}^{(i)} - y^{(i)})^2}$$
$$L(f(\vec{w},b)\vec{x}^{(i)},y^{(i)}) = \begin{cases} -log(f(\vec{w},b)\vec{x}^{(i)}) & \text{si } y^{(i)} = 1 \\ -log(1 - f(\vec{w},b)\vec{x}^{(i)}) & \text{si } y^{(i)} = 0 \end{cases}$$

Nous permet d'obtenir une forme convexe et d'utiliser le gradient descent pour trouver l'optimal local.

Bien entendu, la fonction coût porte sur l'entièreté des données et correspondra donc à la somme des pertes divisées par $m$ :

$$J(\vec{w}, b) = \frac{1}{m} \sum_{i=1}^n L(f(\vec{w},b)\vec{x}^{(i)},y^{(i)})$$

L'algorithme du gradient descent cherchera donc à trouver les paramètres $w,b$ qui minimisent la fonction de coût.

La fonction de perte :

$$L(f(\vec{w},b)\vec{x}^{(i)},y^{(i)}) = \begin{cases} -log(f(\vec{w},b)\vec{x}^{(i)}) & \text{si } y^{(i)} = 1 \\ -log(1 - f(\vec{w},b)\vec{x}^{(i)}) & \text{si } y^{(i)} = 0 \end{cases}$$

Peut être simplifiée comme suit :

$$L(f(\vec{w},b)\vec{x}^{(i)},y^{(i)}) = -y^{(i)}log(f(\vec{w},b)\vec{x}^{(i)})- (1-y^{(i)})log(1-f(\vec{w},b)\vec{x}^{(i)})$$

Elle est simplifiée car elle correspond à la combinaison des deux cas ( $y=1$ ou $y=0$ ) et annule automatiquement un cas si l'autre est en hypothèse.

Si $y^{(i)} =1$ et que nous remplaçons les valeurs des $y$ dans la formule :

$$L(f(\vec{w},b)\vec{x}^{(i)},y^{(i)}) = -\textcolor{blue}{y^{(i)}}log(f(\vec{w},b)\vec{x}^{(i)}) - (1-\textcolor{blue}{y^{(i)}})log(1-f(\vec{w},b)\vec{x}^{(i)})$$
$$L(f(\vec{w},b)\vec{x}^{(i)},y^{(i)}) = -\textcolor{blue}{1}log(f(\vec{w},b)\vec{x}^{(i)}) - (1-\textcolor{blue}{1})log(1-f(\vec{w},b)\vec{x}^{(i)})$$

La partie de droite est annulée car $(1-1)*log... = 0*log... =0$ et donc :

$$L(f(\vec{w},b)\vec{x}^{(i)},y^{(i)}) = \textcolor{blue}{-y^{(i)}log(f(\vec{w},b)\vec{x}^{(i)})}\textcolor{red}{ - (1-y^{(i)})log(1-f(\vec{w},b)\vec{x}^{(i)})}$$

en conséquence, nous obtenons :

$$\textcolor{blue}{-1log(f(\vec{w},b)\vec{x}^{(i)})}$$

Si $y^{(i)} =0$ et que nous remplaçons les valeurs des $y$ dans la formule :

$$L(f(\vec{w},b)\vec{x}^{(i)},y^{(i)}) = -\textcolor{blue}{y^{(i)}}log(f(\vec{w},b)\vec{x}^{(i)}) - (1-\textcolor{blue}{y^{(i)}})log(1-f(\vec{w},b)\vec{x}^{(i)})$$
$$L(f(\vec{w},b)\vec{x}^{(i)},y^{(i)}) = -\textcolor{blue}{0}log(f(\vec{w},b)\vec{x}^{(i)}) - (1-\textcolor{blue}{0})log(1-f(\vec{w},b)\vec{x}^{(i)})$$

La partie de droite est annulée car $-0*log... = 0*log... =0$ et donc :

$$L(f(\vec{w},b)\vec{x}^{(i)},y^{(i)}) = \textcolor{red}{-y^{(i)}log(f(\vec{w},b)\vec{x}^{(i)})}\textcolor{blue}{ - (1-y^{(i)})log(1-f(\vec{w},b)\vec{x}^{(i)})}$$

en conséquence, nous obtenons :

$$\textcolor{blue}{-log(1 - f(\vec{w},b)\vec{x}^{(i)})}$$

Rappelons-nous que la fonction de perte est une partie isolée de la fonction coût ( en bleu ) :

$$J(\vec{w}, b) = \min \left( \frac{1}{m} \sum_{i=1}^n \textcolor{blue}{\frac{1}{2}((\vec{w} \cdot \vec{x}^{(i)} + b) - y^{(i)})^2} \right)$$

Fonction coût corrigée ( convexe )

Par conséquent, si nous souhaitons réécrire l'entièreté de la fonction coût, de petites transformation seront réalisées au niveau des opérateur et nous obtiendrons comme formule finale :

$$J(\vec{w}, b) = -\frac{1}{m} \sum_{i=1}^n y^{(i)}log(f(\vec{w},b)\vec{x}^{(i)}) + (1-y^{(i)})log(1-f(\vec{w},b)\vec{x}^{(i)})$$

Cette fonction de coût finale est dérivée du principe de l'estimation de la probabilité maximale qui permet dans le cadre d'une régression logistique de trouver les paramètres $w$ et $b$ dans une forme convexe.

Fonction coût corrigée ( convexe ) en python

def compute_cost(X, y, w, b, lambda_= 1):

    m, n = X.shape
    
    cost = 0.
                                              
    for i in range(m):
        z = np.dot(X[i],w)+b
        f_wb = sigmoid(z)
        cost += -y[i]*np.log(f_wb) - (1-y[i])*np.log(1-f_wb)
    total_cost = cost/m
    #reg_cost = (lambda_ / (2 * m)) * np.sum(np.square(w))
    #total_cost += reg_cost

    return total_cost

Gradient descent

Tout comme l'algorithme du gradient descent de la régression linéaire , l'objectif du gradient descent dans le cadre de la régression logistique est de trouver le modèle qui minimise la fonction coût $J(\vec{w}, b)$. La définition des valeurs de $w$ et $b$ permettra pour chaque nouvelle valeur de $x$ de définir la probabilité de $y$ d'appartenir à la classe $1$ ( la classe $1$ étant généralement la classe négative ).$P(y = 1 | \vec{X}; \vec{w}, b)$.

$$f(z) = \frac{1}{1 + e^{(-(\vec{w} \cdot \vec{x} + b))}}$$

Le formule complète du coût :

$$J(\vec{w}, b) = \min -\frac{1}{m} \sum_{i=1}^n y^{(i)}log(f(\vec{w},b)\vec{x}^{(i)}) + (1-y^{(i)})log(1-f(\vec{w},b)\vec{x}^{(i)})$$

L'implémentation du gradient pour minimiser le coût correspond au même procédé que la régression linéaire, à savoir :

Pour chaque itération $(i)$, il est important de définir, de manière temporaire la nouvelle valeur de w et la nouvelle valeur de b pour les remplacer par la suite de manière simultanée.

1. $temp_w = w_j - \alpha \frac{d}{dw} J(w, b) = \frac{1}{m} \sum_{i=1}^{m} [f_{w,b}(x^{(i)}) - y^{(i)}] x^{(i)}$ ;
2. $temp_b = b - \alpha \frac{d}{db} J(w, b) = \frac{1}{m} \sum_{i=1}^{m} [f_{w,b}(x^{(i)}) - y^{(i)}]$ ;
3. $w = temp_w$ ;
4. $b = temp_b$ ;

Cette définition des étapes du gradient descent ressemble entièrement à la régression linéaire. C'est tout à fait normal ; Ce qui change est la manière ensuite de définir le modèle :

1. Dans la régression linéaire, nous retrouvons : $f_{\vec{w}, b}(\vec{x}) = \vec{w} \cdot \vec{x} + b$ ;
2. Dans la régression logistique, nous appliquons $f(z)$ soit $f(z) = \frac{1}{1 + e^{(-(\vec{w} \cdot \vec{x} + b))}}$ ;

attention

Même si l'algorithme du gradient descent semble similaire pour la régression linéaire et logistique, il s'agit bien de deux algorithmes différents étant donné la manière dont ils sont introduits par la suite dans le modèle.

Rapport des cotes

En statistique, l'Odd Ratio ( rapport des cotes ), est une mesure permettant de quantifier la force d'association entre une variable explicative ( donc un prédicteur ) et la probabilité d'occurrence de l'évènement que l'on souhaite prédire ( pour rappel, il s'agit de la classe positive $1$ qui signifie l'aspect négatif (Spam 1 , Non Spam 0 ; Malade 1 ; Non Malade 0 etc) ).

Le rapport des cotes évalue la variation de la probabilité de $y=1$ en fonction d'une augmentation d'une unité de la variable explicative.

imaginons que nous avons $10$ Patients. Sur les $10$ patients, $6$ sont malades et $4$ patients ont de la fièvre. Parmi les patients qui ont de la fièvre, $3$ sont malades et $1$ ne l'est pas. Le rapport des cotes va nous permettre de calculer la chance d'avoir de la fièvre quand on est malade par rapport au fait de ne pas être malade et avoir de la fièvre.

	Fièvre	Pas de fièvre	Total
Malade	3 (p)	3	6
Pas Malade	1 (q)	3	4
Total	4	6	10

Pour calculer le rapport des cotes, nous utilisons la formule suivante ( où $p$ est la proportion de malades ayant de la fièvre et $q$ est la proportion de non-malades ayant de la fièvre ) :

$$OR = \frac{\frac{p}{(1 - p)}}{\frac{q}{(1 - q)}} = \frac{p(1 - q)}{q(1 - p)}$$

Dans notre exemple : $p = 3/6$ soit $0,5 ; q = 1/4$ soit $0,25$

Soit :

$$\frac{\frac{0,5}{(1 - 0,5)}}{\frac{0,25}{(1 - 0,25)}} = \frac{0,5(1 - 0,25)}{0,25(1 - 0,5)} = \frac{1}{0,333} = 3$$

Concernant le résultat obtenu, il représente le fait que les patients malades ont 3 fois plus de chance d'avoir de la fièvre que les patients non malades.

attention

Cela ne signifie pas la probabilité d'avoir de la fièvre si on est malade ou d'être malade si on a de la fièvre ! Il s'agit simplement de l'association entre la maladie et la fièvre

En régression logistique, le rapport des cotes est calculé à partir du coefficient $w$ trouvé par la méthode du gradient descent. Le rapport des cotes pour une variable explicative est donné par $e^{w}$. Par exemple, si le gradient descent identifie une valeur de $w$ de $0,03$ pour la fièvre, le rapport des cotes est donc $e^(0,03) = 1.03$. Cela signifie que les chances d'être malade augmentent de $3%* lorsqu'un patient a de la fièvre par rapport à un patient qui n'en a pas.

Toutefois, le rapport des chances ne sert pas dans le calcul de la probabilité mais permet de mieux comprendre le facteur multiplicatif de chance que l'évènement diminue ou augmente lorsque la variable explicative augmente d'une unité. Il permet donc de comparer plus facilement l'impact des différentes variables explicatives sur la probabilité de l'évènement.

Le rapport des chances permet de mieux comprendre le fonctionnement du modèle et les résultats.

Pour rappel, la probabilité sera calculée sur base de la valeur de $x$ d'un nouvel enregistrement et des valeurs de $b$ et $w$ identifiés par le gradient descent.

Gradient descent en python :

def compute_gradient(X, y, w, b, lambda_=1):

    m, n = X.shape
    dj_dw = np.zeros(w.shape)
    dj_db = 0.

    for i in range(m):
        f_wb_i = sigmoid(np.dot(X[i],w) + b)          
        err_i  = f_wb_i  - y[i]                      
        for j in range(n):
            dj_dw[j] = dj_dw[j] + err_i * X[i,j]     
    dj_db = dj_db + err_i
    dj_dw = dj_dw/m                                  
    dj_db = dj_db/m                                  
    dj_dw += (lambda_ / m) * w
    return dj_db, dj_dw

Lancement du gradient descent:

def gradient_descent(X, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters, lambda_):


    m = len(X)

    J_history = []
    w_history = []

    for i in range(num_iters):

        dj_db, dj_dw = gradient_function(X, y, w_in, b_in, lambda_)

        w_in = w_in - alpha * dj_dw
        b_in = b_in - alpha * dj_db
        
        if i<100000:      
            J_history.append( cost_function(X, y, w_in, b_in, lambda_))
        
        if i > 1 and abs(J_history[-1] - J_history[-2]) < 0.000001:
            print(f"Early stopping at iteration {i} as cost change is less than 0.000001")
            break 
            
        if i% math.ceil(num_iters / 10) == 0:
            print(f"Iteration {i:4}: Cost {J_history[-1]} ",
                  f"dj_dw: {dj_dw}, dj_db: {dj_db}  ",
                  f"w_in: {w_in}, b_in:{b_in}")

    return w_in, b_in, J_history, w_history 


np.random.seed(1)
initial_w = np.zeros(X_train.shape[1])  
initial_b = 0

lambda_=0.01
iterations = 1000
alpha = 0.003

w,b, J_history,_ = gradient_descent(X_train ,y_train, initial_w, initial_b,
                                   compute_cost, compute_gradient, alpha, iterations, lambda_)

$$f(z) = \frac{1}{1 + e^{(-(\vec{w} \cdot \vec{x} + b))}}$$

Régularisation

Le principe de régularisation d'une régression logistique est identique à ce que l'on retrouve pour de la fonction linéaire.

C'est à dire que dans le cadre d'un sous-apprentissage, l'option principale est d'ajouter des variables ou des enregistrements supplémentaires et en sur-apprentissage nous retrouvons également les options de base telles que l'augmentation ou la réduction de variables ( Sélection des Variables ) et l'augmentation des enregistrements.

Comme dans le cadre de la régression linéaire, la réduction du nombre de variables s'applique via le concept de l'ingénierie des caractéristiques ou par l'utilisation spécifiques de techniques.

Si pour des raisons spécifiques, nous devons en tant que data scientist, maintenir la sélection de toutes les variables, nous pouvons également palier au sur-apprentissage par l'application de la régularisation pour la régression logistique.

Rappelons que le concept de régularisation consiste à réduire l'impact de certaines variables par l'attribution d'un poids plus faible. Concrètement, l'idée est de faire en sorte que l'algorithme d'apprentissage réduise les valeurs des paramètres sans pour autant exiger de mettre des paramètres à $0$. La régularisation s'applique principalement aux valeurs de $w$ même si l'on pourrait également considérer une régularisation sur le paramètre $b$.

Cette pénalisation se fait par l'ajout de la régularisation suivante à la fonction coût modifiée de la régression logistique :

$$J(\vec{w}, b) = \min -\frac{1}{m} \sum_{i=1}^n y^{(i)}log(f(\vec{w},b)\vec{x}^{(i)}) + (1-y^{(i)})log(1-f(\vec{w},b)\vec{x}^{(i)}) + \textcolor{blue}{\frac{\lambda}{2m} \sum_{j=1}^n w_j^2}$$

astuce

Gradient descent régularisé

$J(\vec{w}, b) = \min -\frac{1}{m} \sum_{i=1}^n y^{(i)}log(f(\vec{w},b)\vec{x}^{(i)}) + (1-y^{(i)})log(1-f(\vec{w},b)\vec{x}^{(i)}) + \textcolor{blue}{\frac{\lambda}{2m} \sum_{j=1}^n w_j^2}$

1. $temp_w = w - \alpha \frac{d}{dw} J(w, b) = w - \alpha \left( \frac{1}{m} \sum_{i=1}^{m} [f_{w,b}(x^{(i)}) - y^{(i)}] x^{(i)} + \textcolor{blue}{\frac{\lambda}{m} w_j}\right)$ ;
2. $temp_b = b - \alpha \frac{d}{db} J(w, b) = b - \alpha \left( \frac{1}{m} \sum_{i=1}^{m} [f_{w,b}(x^{(i)}) - y^{(i)}]\right)$;
3. $w = temp_w$ ;
4. $b = temp_b$ ;

Code python complet

import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import math, copy
from sklearn.metrics import confusion_matrix



data = pd.read_csv('data.csv')
data

x = data[['x_1', 'x_2', 'x_3', 'x_4', 'x_5', '...', 'x_n']].values  
y = data['y'].values  


scaler_x = StandardScaler()
scaler_y = StandardScaler()

x = scaler_x.fit_transform(x)
y = scaler_y.fit_transform(y.reshape(-1, 1))

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4, random_state=42)

#polynomial
"""
# Chargement des données
data = pd.read_csv('data.csv')

# Séparation des caractéristiques et de la cible
x = data[['x_1', 'x_2', 'x_3', 'x_4', 'x_5', '...', 'x_n']].values  
y = data['y'].values  

# Génération des termes polynomiaux de degré 3
poly = PolynomialFeatures(degree=3)
x_poly = poly.fit_transform(x)

# Standardisation des données polynomiales
scaler_x = StandardScaler()
x_poly = scaler_x.fit_transform(x_poly)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4, random_state=42)
"""
# /Polynomial

def sigmoid(z):

    g = 1/(1+np.exp(-z))


    return g


def compute_cost(X, y, w, b, lambda_= 1):

    m, n = X.shape
    
    cost = 0.
                                              
    for i in range(m):
        z = np.dot(X[i],w)+b
        f_wb = sigmoid(z)
        cost += -y[i]*np.log(f_wb) - (1-y[i])*np.log(1-f_wb)
    total_cost = cost/m

    reg_cost = (lambda_ / (2 * m)) * np.sum(np.square(w))
    total_cost += reg_cost

    return total_cost

def compute_gradient(X, y, w, b, lambda_=1):

    m, n = X.shape
    dj_dw = np.zeros(w.shape)
    dj_db = 0.

    for i in range(m):
        f_wb_i = sigmoid(np.dot(X[i],w) + b)          
        err_i  = f_wb_i  - y[i]                      
        for j in range(n):
            dj_dw[j] = dj_dw[j] + err_i * X[i,j]     
    dj_db = dj_db + err_i
    dj_dw = dj_dw/m                                  
    dj_db = dj_db/m                                  
    dj_dw += (lambda_ / m) * w
    return dj_db, dj_dw


def gradient_descent(X, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters, lambda_):


    m = len(X)

    J_history = []
    w_history = []

    for i in range(num_iters):

        dj_db, dj_dw = gradient_function(X, y, w_in, b_in, lambda_)

        w_in = w_in - alpha * dj_dw
        b_in = b_in - alpha * dj_db
        
        if i<100000:      
            J_history.append( cost_function(X, y, w_in, b_in, lambda_))
        
        if i > 1 and abs(J_history[-1] - J_history[-2]) < 0.000001:
            print(f"Early stopping at iteration {i} as cost change is less than 0.000001")
            break 
            
        if i% math.ceil(num_iters / 10) == 0:
            print(f"Iteration {i:4}: Cost {J_history[-1]} ",
                  f"dj_dw: {dj_dw}, dj_db: {dj_db}  ",
                  f"w_in: {w_in}, b_in:{b_in}")

    return w_in, b_in, J_history, w_history 


np.random.seed(1)
initial_w = np.zeros(X_train.shape[1])  
initial_b = 0

lambda_=0.01
iterations = 1000
alpha = 0.003

w,b, J_history,_ = gradient_descent(X_train ,y_train, initial_w, initial_b,
                                   compute_cost, compute_gradient, alpha, iterations, lambda_)

def predict(X, w, b):

    m, n = X.shape
    p = np.zeros(m)

    for i in range(m):
        z_wb = np.dot(X[i],w)
        
        for j in range(n):
            
            z_wb += 0

        z_wb += b

        f_wb = sigmoid(z_wb)

        p[i] =  1 if f_wb>0.5 else 0

    return p


p = predict(X_test, w, b) 
confusion = confusion_matrix(y_test, p)


TP = confusion[1, 1]  # True positive
FP = confusion[0, 1]  # False positive
TN = confusion[0, 0]  # True negative
FN = confusion[1, 0]  # False negzative

print("Confusion matrix :")
print(confusion)
print("True positive (TP):", TP)
print("False positive (FP):", FP)
print("True negative (TN):", TN)
print("False negzative (FN):", FN)