Arbre de décision

L'arbre de décision est l'une des techniques les plus puissantes en apprentissage supervisé et pourrait être élevé au rang des réseaux de neurones, si ces deux techniques faisaient partie de la même famille.

Nous avons vu jusqu'à présent des techniques dites « paramétriques », c'est à dire des techniques dont l'apprentissage a pour objectif d'identifier des paramètres expliquant une relation entre des variables explicatives ( prédicteurs ) $x_1$ et une variable expliquée ( ou prédite ), $y$. L'identification de ces paramètres est réalisée par un ensemble d'itérations dont l'objectif est de réduire une fonction coût.

l'arbre de décision est une technique non paramétrique, ce qui signifie qu'il n'y a pas de paramètres expliquant la relation entre les $x$ et $y$. Il s'agit d'une des techniques les plus utilisée car elle est facilement compréhensible ( interprétable ) et peut faire face à des données manquantes.

La technique d'arbre dans laquelle la variable cible est qualitative est appelée « arbre de classement » et celle pour laquelle la variable cible contient des valeurs quantitatives est appelée « arbre de régression ».

Appliquer un modèle d’arbre de décision consiste à partir de l’ensemble des données pour ensuite les diviser récursivement en cellules de plus en plus petites qui sont de plus en plus pures dans le sens où elles ont des valeurs similaires à la cible. Les données sont divisées en segments sur base de règles de fractionnement à chaque étape. Considérées dans leurs entièretés, les règles de l’ensemble des segments forment le modèle d’arbre de décision.

Un arbre de décision est donc un ensemble hiérarchique de règles décrivant les divisions successives d’un grand ensemble de données en groupes de plus petits enregistrements. À chaque division successive, les membres des segments résultants sont de plus en plus ressemblants jusqu’à ce qu’à ce qu’ils puissent être assimilés à la variable cible.

Pour pouvoir bénéficier d’un modèle d’arbre de décision précis, l’algorithme doit s’appuyer sur un nombre d’enregistrements important. Toutefois et contrairement à d’autres techniques, lorsque les arbres sont construits, les calculs ne sont pas gourmands en termes de performances. De plus, l’arbre de décision est une technique hautement automatisée, résistante aux valeurs aberrantes et capable de gérer les valeurs manquantes.

L’une des raisons pour lesquelles les arbres de décision sont très populaires, c’est qu’ils fournissent des règles de décision facilement compréhensibles. IF Age ≤ 55 AND Education > 12 THEN Class = 1 ELSE ; Chaque sous-groupe résultant de la division contient un ensemble d’enregistrements homogènes

remarque

Certains schémas et concepts présentés ici sont inspirés du cours Machine Learning d'Andrew Ng, programme créé en collaboration entre Stanford university Online Education et DeepLearning.AI disponible sur Coursera. Retrouvez le cours original ici : Machine Learning by Andrew Ng.

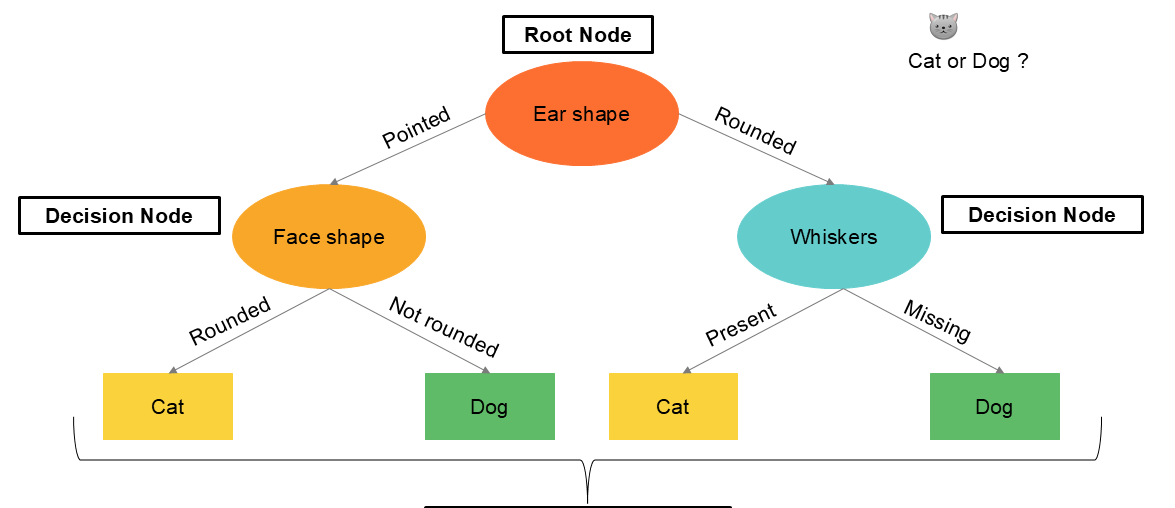
Structure

Un arbre de décision commence toujours au niveau du noeud racine - root node - qui contient tous les enregistrements. L'arbre va tester toutes les variables du modèle dans le noeud racine afin d'identifier la variable qui sépare au mieux les données. Les données sont ensuite répartie dans deux noeuds de décision qui, à leur tour vont tester toutes les variables pour identifier la meilleure répartition de l'information en « une information plus pure ». Ces divisions sont répétées et à chaque étape, soit l'information se retrouve dans un nouveau noeud de décision ( nouvelle division des enregistrements ) soit dans un noeud terminal où l'information est considérée comme ayant atteint une certaine pureté.

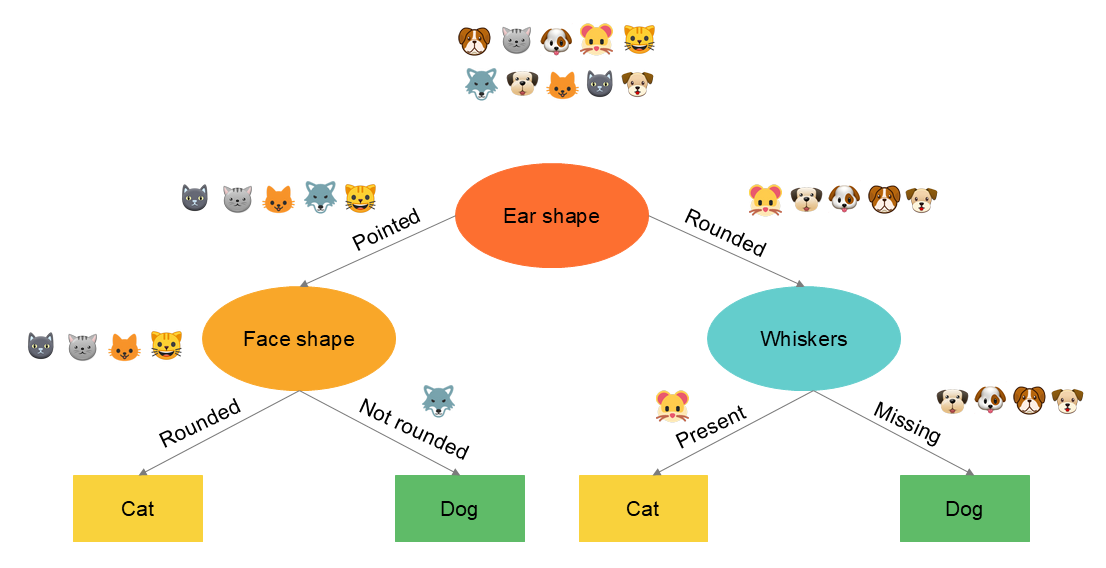
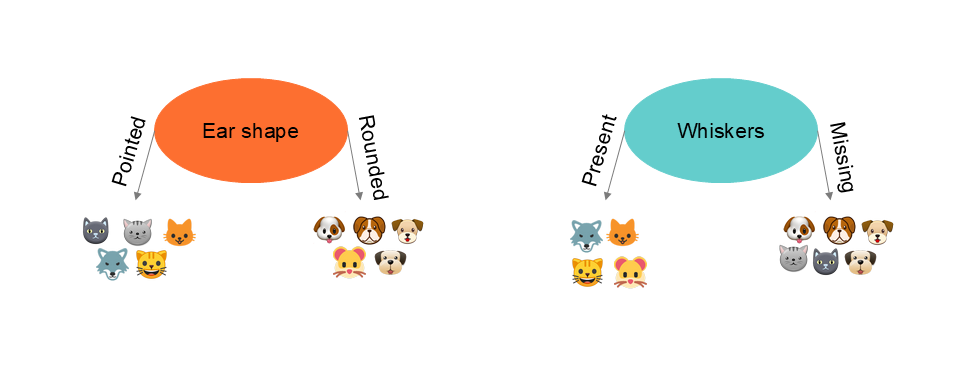
Prenons l'exemple suivant pour illustrer un arbre de décision. Nous commencerons par un arbre de classement. Nous disposons de données concernant des chats et des chiens et nous souhaitons entrainer un algorithme d’arbre de décision pour prédire si un nouvel animal est un chien ou un chat au regard de ses caractéristiques. Notre set de données contient trois variables qualitatives ( qui normalement devraient être transformée en encodage one-hot ) ainsi qu'une variable $y$ reprenant la valeur $1$ lorsqu'il s'agit d'un chat et la valeur $0$ lorsqu'il s'agit d'un chien.

Forme de l'oreille x1	Forme du visage x2	Moustache x3	Chat y
Pointue	Arrondie	Présente	1
Flottante	Pas arrondie	Présente	1
Flottante	Arrondie	Absente	0
Pointue	Pas arrondie	Présente	0
Pointue	Arrondie	Présente	1
Pointue	Arrondie	Absente	1
Flottante	Pas arrondie	Absente	0
Pointue	Arrondie	Absente	1
Flottante	Arrondie	Absente	0
Flottante	Arrondie	Absente	0

Pour une nouvel enregistrement, nous souhaitons un modèle qui nous permet d'identifier s'il s'agit du chien ou d'un chat.

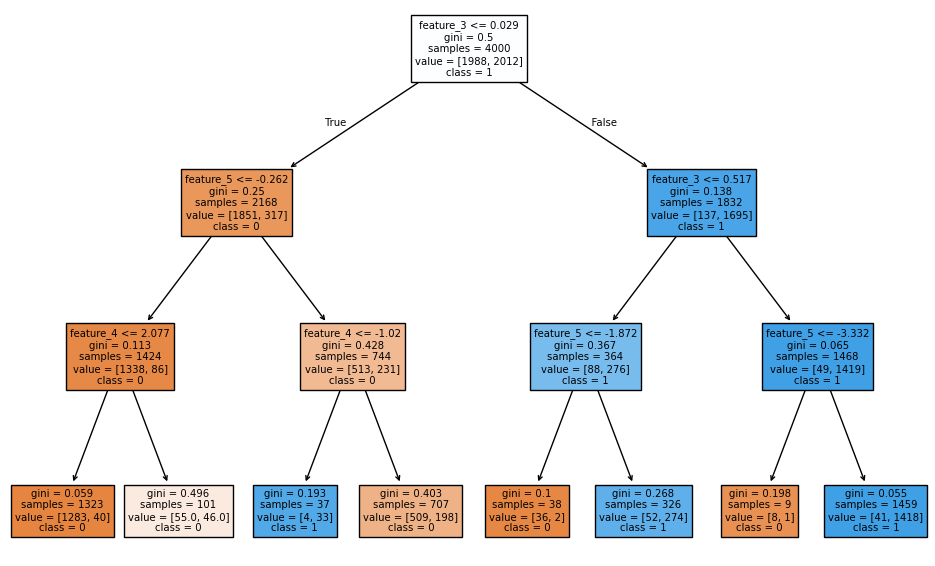
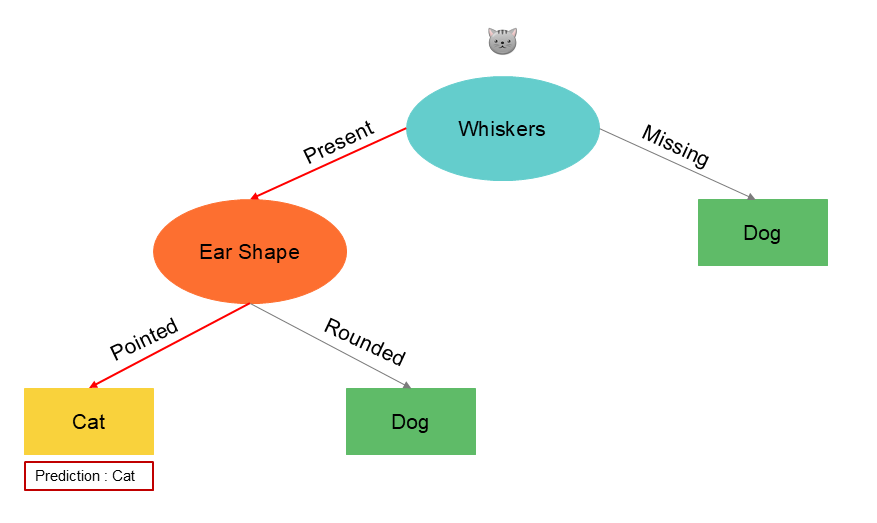
Voici l'exemple d'un modèle entrainé dans notre cas :

Partitionnement récursif

Le concept clé de la construction d’un arbre est le partitionnement récursif des informations. Il s’agit en fait de regrouper les enregistrements en les divisant en sous-population en fonction d’une valeur de répartition. Cette division est accomplie récursivement c'est à dire en opérant sur les résultats de la division précédente.

La récursivité signifie que l'on construit un arbre de décision à la racine en construisant d'autres arbres de décision plus petits dans les sous-branches de gauche et de droite. Toutes les variables sont à chaque fois considérées pour identifier celle qui divisera au mieux les informations, c'est à dire qui permettra d'obtenir des noeuds plus pures après répartition.

En informatique, la récursivité consiste à écrire un code qui s'appelle lui-même. Dans le cadre de la construction d'un arbre de décision, on construit l'arbre de décision global en construisant des sous-arbres de décision plus petits, puis en les rassemblant. C'est pourquoi les implémentations logicielles d'arbres de décision font parfois référence à un algorithme récursif.

Ce partitionnement s'effectue selon une définition - choix arbitraire du data scientist - sur la profondeur de l'arbre. Plus la profondeur maximale est grande, plus l'arbre de décision est grand. Ce qui laisse la possibilité à l’arbre de décision d’apprendre un modèle plus complexe mais également d’augmenter le risque de surapprentissage.

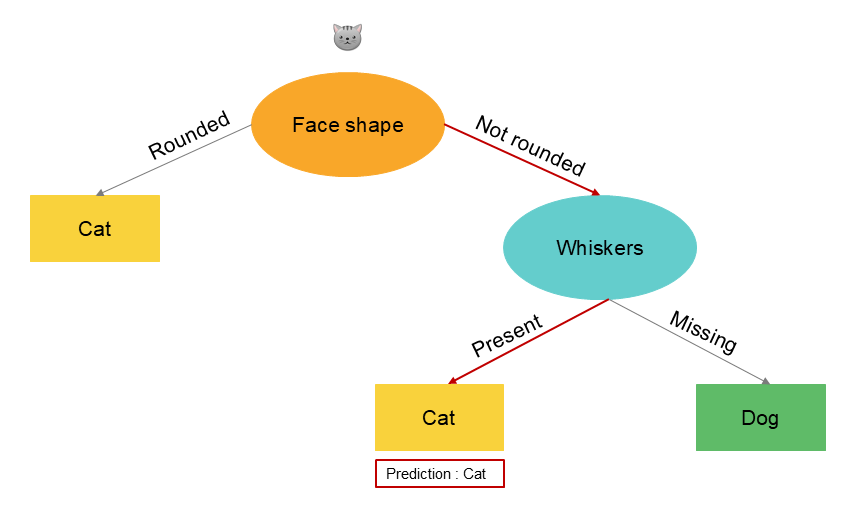
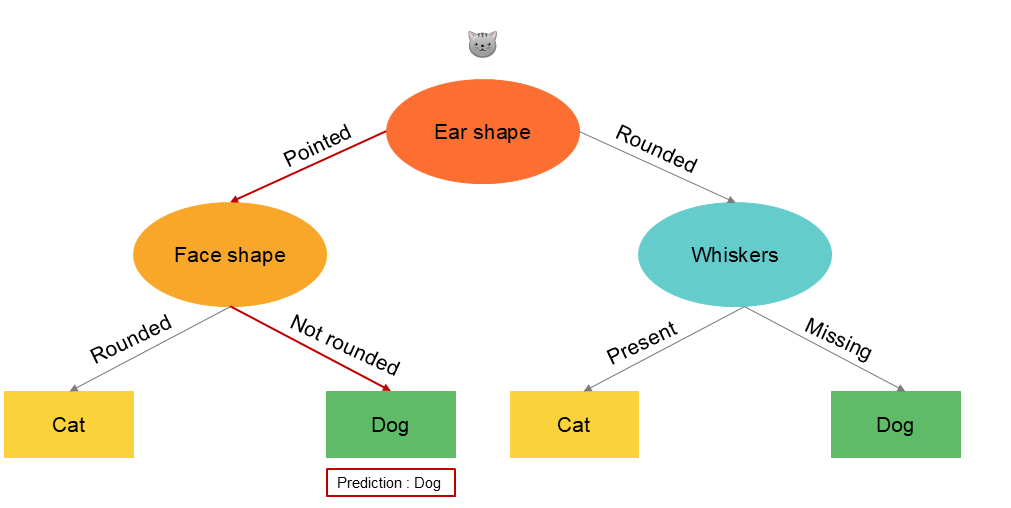
Il existe donc différentes manières de créer un arbre de décision. Voici quelques exemples d’alternatives dans notre cas illustré. Parmi ces versions certaines seront meilleures que notre arbre de base, d’autres moins bonnes lorsque l’on évaluera le modèle sur les données de test. Nous sélectionnerons celui qui sera le plus performant mais également qui aura une règle généralisable.

Processus d'apprentissage

Les étapes de l’arbre de décision peuvent être reprises comme suit :

Nous désignons la variable de sortie ( cible ) y et les variables d’entrée ( prédicteurs ) $𝑋_1 , 𝑋_2 , 𝑋_3, … , 𝑋_𝑝$. Les prédicteurs peuvent être quantitatifs ou qualitatifs mais dans ce dernier cas devront être transformés par la technique de l'encodage one-hot s'il s'agit de variables qualitatives nominales et numérisées s'il s'agit de variables qualitatives ordinales

• Étape 1 : nous démarrons avec tous les enregistrements dans le nœud racine
• Étape 2 : calcul du gain de l’information pour tous les 𝑋_𝑖 et sélection de la variable dont le gain est le plus élevé
• Étape 3 : pour cette variable 𝑋_𝑖, séparation des enregistrements dans une branche gauche (nœud de décision gauche) ou une branche droite (nœud de décision droite)
• Étape 4 : répétition du processus jusqu’à ce qu’un critère d’arrêt soit rencontré

La première décision de l’algorithme est de définir quelle est la variable $x$ qui sera considérée dans le noeud racine afin de créer la première répartition des données. Quelles seront ensuite les variables $x$ qui seront considérées dans les subdivisions des noeuds suivants jusqu'aux feuilles terminales.

Le choix de la variable d’entrée pour la répartition du noeud racine est primordiale car il va permettre une première répartition des données en sous-groupes contenant des valeurs plus homogènes. La question est donc d’identifier comment choisir l’arborescence des variables d’entrée.

Autrement dit : quel est le meilleur noeud racine et quels sont les meilleurs enfants d’un noeud parent ? Le but étant de séparer autant que possible les valeurs de la cible, l’algorithme va considérer tous les fractionnements possibles sur toutes les variables d’entrée sur base de la meilleure valeur de répartition.

L'objectif de l'algorithme est donc d'identifier la première variable qui maximise la pureté ou minimise l’impureté.

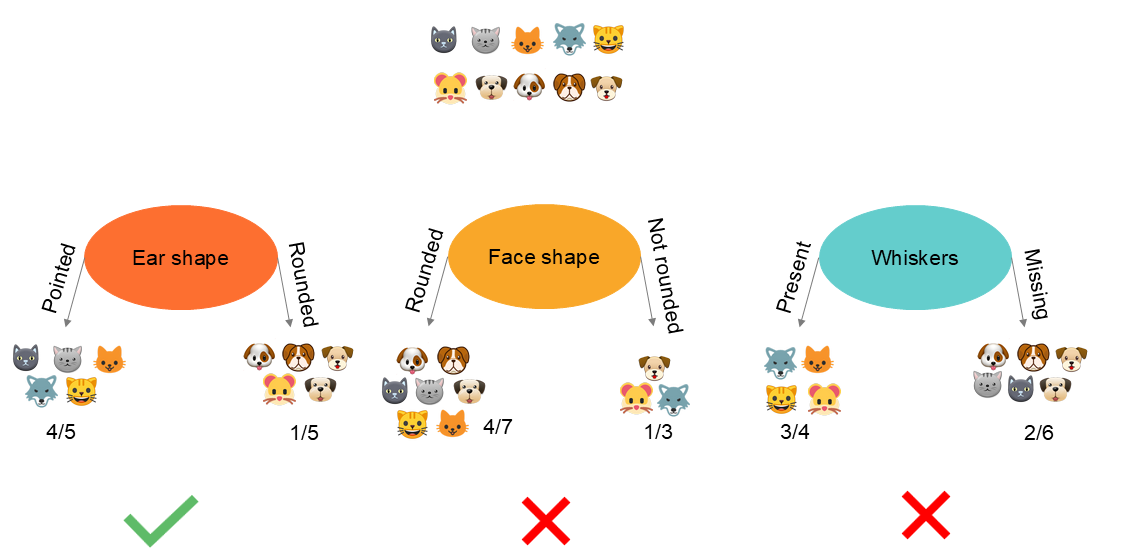
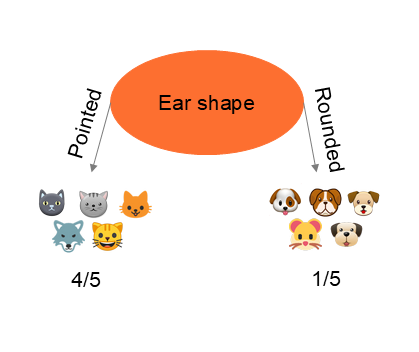
Dans le cas ci-dessus, nous constatons que la réalisation d'un partitionnement de l'information sur base de la forme des oreilles permet une répartition plus pure, c'est à dire d'obtenir la meilleur séparation entre les chats et les chiens. Cet exemple est relativement simple, car nous visualisons le résultat. Il existe bien entendu des indicateurs

Mesure de l'impureté

L'objectif d'un arbre est donc d’obtenir des nouveaux noeuds plus « pures » après subdivision des informations. L’impureté est un indice qui va nous permettre d’identifier le noeud résultant qui contient le plus de valeurs homogènes. L'impureté est évaluée par la mesure de l’Entropie.

Probabilité :

$$p_0 = 1 - p_1$$

Entropie:

$$H(p_1)$$
$$= -p_1 \log_2(p_1) - p_0 \log_2(p_0)$$
$$= -p_1 \log_2(p_1) - (1 - p_1) \log_2(1 - p_1)$$

Commençons par calculer l'entropie, c'est à dire la mesure de l'impureté. Le principe est le suivant : un plus un noeud contient des valeurs semblables, au plus il est pure.

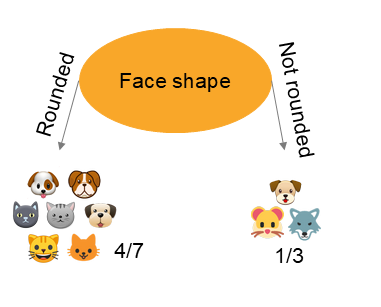
Prenons l'exemple suivant de quatre prédicteurs ( forme des oreilles $x_1$ , forme du visage $x_2$ , ... , présence de moustache $x_4$ ) qui ont été utilisé pour répartir les informations. Dans le première situation, le noeud résultant de l'opération contient 2 chats et 4 chiens. $P_1$ correspond donc à $\frac{2}{6}$. Dans le second cas, le noeud résultant de l'opération contient 3 chats et 3 chiens. $P_1$ correspond donc à $\frac{3}{6}$. Nous connaissons donc $P_1$ pour chaque cas et nous devons calculer la formule de l'entropie sachant que $p_0 = 1 - p_1$. Nous obtenons les valeurs suivantes :

Le détail du calcul de l'entropie pour chaque cas :

$$-\frac{2}{6} \cdot \log_2 \left( \frac{2}{6} \right) - \frac{4}{6} \cdot \log_2 \left( \frac{4}{6} \right) = 0.92$$ $$-\frac{3}{6} \cdot \log_2 \left( \frac{3}{6} \right) - \frac{3}{6} \cdot \log_2 \left( \frac{3}{6} \right) = 1.00$$ $$-\frac{5}{6} \cdot \log_2 \left( \frac{5}{6} \right) - \frac{1}{6} \cdot \log_2 \left( \frac{1}{6} \right) = 0.65$$ $$-\frac{6}{6} \cdot \log_2 \left( \frac{6}{6} \right) - \frac{0}{6} \cdot \log_2 \left( \frac{0}{6} \right) = 0.00$$

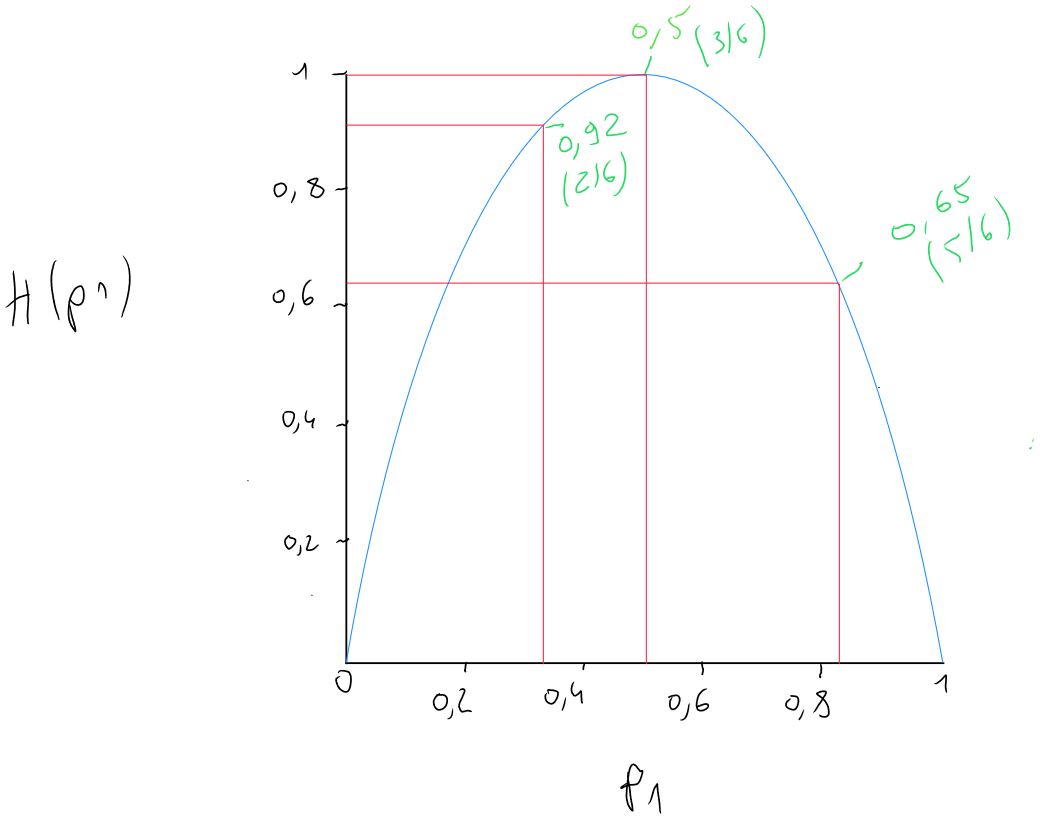
Nous constatons que lorsque nous obtenons un groupe comprenant la moitié de chat et la moitié de chien, l'entropie est égale à 1. L'entropie est à son maximum, c'est à dire que nous sommes dans un impureté complète. Le noeud est hétérogène ( nous souhaitons un noeud homogène c'est à dire ne contenant que des chiens ou des chats ). A contrario, lorsque nous obtenons un noeud complètement homogène ( uniquement des chats ), nous constatons que l'entropie est égale à $0$, nous sommes dans une pureté complète.

Nous pouvons représenter graphiquement ces exemples en reprenant en axe des abscisses la probabilité $P_1$ et en ordonnée la valeur de l'entropie pour constater l'impact de la probabilité $p_1$ et les différents cas.

Gain d'information

L'entropie nous permet donc de calculer l'impureté mais ce qui nous intéresse, c'est d'identifier parmi les variables, celle qui va nous permettre de réduire cette impureté. La réduction de l’entropie s’appelle « le gain d’information ». Le gain d'information correspond au résultat du passage d'un état $A$, à un état $B$. Autrement dit : du noeud racine, dans laquelle nous retrouvons tous nos enregistrements au noeud suivant. Imaginons que nous avons 5 chats et 5 chiens, nous avons donc une entropie de 1 qui correspond à la fonction $H(0.5)$ ( 5 chats / 5 chiens donc p1 = 5/10 = 0.5 et H(0.5) = 1 ).

Nous démarrons donc d'une valeur $H(0.5) - noeud racine - sur laquelle nous allons calculer le résultat de la soustraction de l'entropie des deux noeuds résultants après utilisation d'une variable comme étant séparateur.

Cas numéro 1

$p_1 = \frac{4}{5} = 0.8 \qquad p_0 = \frac{1}{5} = 0.2$

$H(0.8) = 0.72 \qquad H(0.2) = 0.72$

$H(0.5) - \left( \frac{5}{10} H(0.8) + \frac{5}{10} H(0.2) \right)$

$= 1 - \left( 0.5 \cdot 0.72 + 0.5 \cdot 0.72 \right)$

$= 1 - 0.72$

Gain information$= 0.28$

Cas numéro 2

$p_1 = \frac{4}{7} = 0.57 \qquad p_0 = \frac{1}{3} = 0.33$

$H(0.57) = 0.99 \qquad H(0.33) = 0.92$

$H(0.5) - \left( \frac{7}{10} H(0.57) + \frac{3}{10} H(0.33) \right)$

$= 1 - \left( 0.7 \cdot 0.99 + 0.3 \cdot 0.92 \right)$

$= 1 - 0.97$

Gain information$= 0.03$

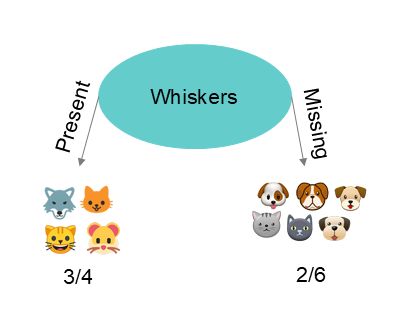
Cas numéro 3

$p_1 = \frac{3}{4} = 0.75 \qquad p_0 = \frac{2}{6} = 0.33$

$H(0.75) = 0.81 \qquad H(0.33) = 0.92$

$H(0.5) - \left( \frac{4}{10} H(0.75) + \frac{6}{10} H(0.33) \right)$

$= 1 - \left( 0.4 \cdot 0.81 + 0.6 \cdot 0.92 \right)$

$= 1 - 0.88$

Gain information$= 0.12$

Le cas numéro $1$ obtient un gain d'information de $0.28$ après répartition des enregistrements sur base de la variable sur la forme des oreilles dans deux nouveaux noeuds. Il s'agit donc de la meilleure variable de répartition. L'opération va ensuite se répété pour chaque subdivision suivante.

astuce

La gain d'information se calcule donc comme suit :

• (1) Valeur de l'entropie du noeud de départ ( avant répartition dans les noeuds de gauche et de droite )
• (2) Nombre de valeurs Y=1 dans le noeud de décision final de gauche / nombre de valeurs total dans le noeuds de départ
• (3) Entropie du nombre de valeurs y=1 dans le noeud de décision final de gauche / nombre de valeurs total dans le noeud de décision de gauche
• (4) Nombre de valeurs Y=1 dans le noeud de décision final de droite/ nombre de valeurs total dans le noeuds de départ
• (5) Entropie du nombre de valeurs y=1 dans le noeud de décision final de droite / nombre de valeurs total dans le noeud de décision de droite

$$(1) - ((2) * (3)) + ((4) * (5))$$
$$H(Nr) - \left( \frac{Nr}{Nr} H(Nr) + \frac{Nr}{Nr} H(Nr) \right)$$


Exemple :

$$H(0.5) - \left( \frac{4}{10} H(0.75) + \frac{6}{10} H(0.33) \right)$$

Profondeur de l'arbre

L'algorithme de l'arbre va donc subdiviser chaque noeuds en de nouveaux noeuds inférieurs ( à gauche et à droite ) dont l'information sera à chaque division plus pure. L'une des questions fondamentale de la création ( la seconde questions la plus importante après la définition de la pureté ), est de savoir jusque quel niveau l'algorithme doit descendre, c’est-à-dire à partir de quel moment il arrête de créer des subdivisions ?

• Lorsqu’un nœud contient 100 % de la même classe ( classement ) ; Lorsque la variance d'un noeud est inférieure ou égale à un certain seuil ( estimation ) ;
• Lorsque la séparation d’un nœud excède le maximum de profondeur souhaité ;
• Lorsque l’amélioration du score de pureté est inférieure à un seuil ;
• Lorsque le nombre d’exemples dans un nœud est inférieur à un seuil ;

Prédicteur qualitatif

Les variables qualitatives doivent être converties en une représentation numérique avant de pouvoir être utilisées dans le processus de construction de l'arbre en tant que prédicteur.

Si les variables sont de type qualitatives ordinales, elle doivent être numérisées. Si les variables sont de type qualitatives nominales, nous devons procéder à un encodage one-hot.

Prédicteur quantitatif

Lorsque nous disposons de prédicteurs quantitatifs, l’algorithme de l’arbre de décision fonctionnera de la même manière en ce qui concerne la répartition de l'information, c’est-à-dire qu’il analysera la meilleure répartition des données pour un meilleur gain d’information. Toutefois, comme nous ne disposons pas de classes, l'algorithme utilisera la valeur de la médiane de chaque paires de valeurs consécutives du set de données et sélectionnera celles qui permet d'obtenir le meilleur gain d'information.

Prenons l'exemple d'une nouveau prédicteur dans notre set de données pour notre arbre de classement, à savoir le poids.

Forme de l'oreille x1	Forme du visage x2	Moustache x3	Poids x4	Chat y
Pointue	Arrondie	Présente	7.2	1
Flottante	Pas arrondie	Présente	8.8	1
Flottante	Arrondie	Absente	15	0
Pointue	Pas arrondie	Présente	9.2	0
Pointue	Arrondie	Présente	8.4	1
Pointue	Arrondie	Absente	7.6	1
Flottante	Pas arrondie	Absente	11	0
Pointue	Arrondie	Absente	10.2	1
Flottante	Arrondie	Absente	18	0
Flottante	Arrondie	Absente	20	0

attention

Les données doivent être triées sur base de la variable quantitative par ordre croissant

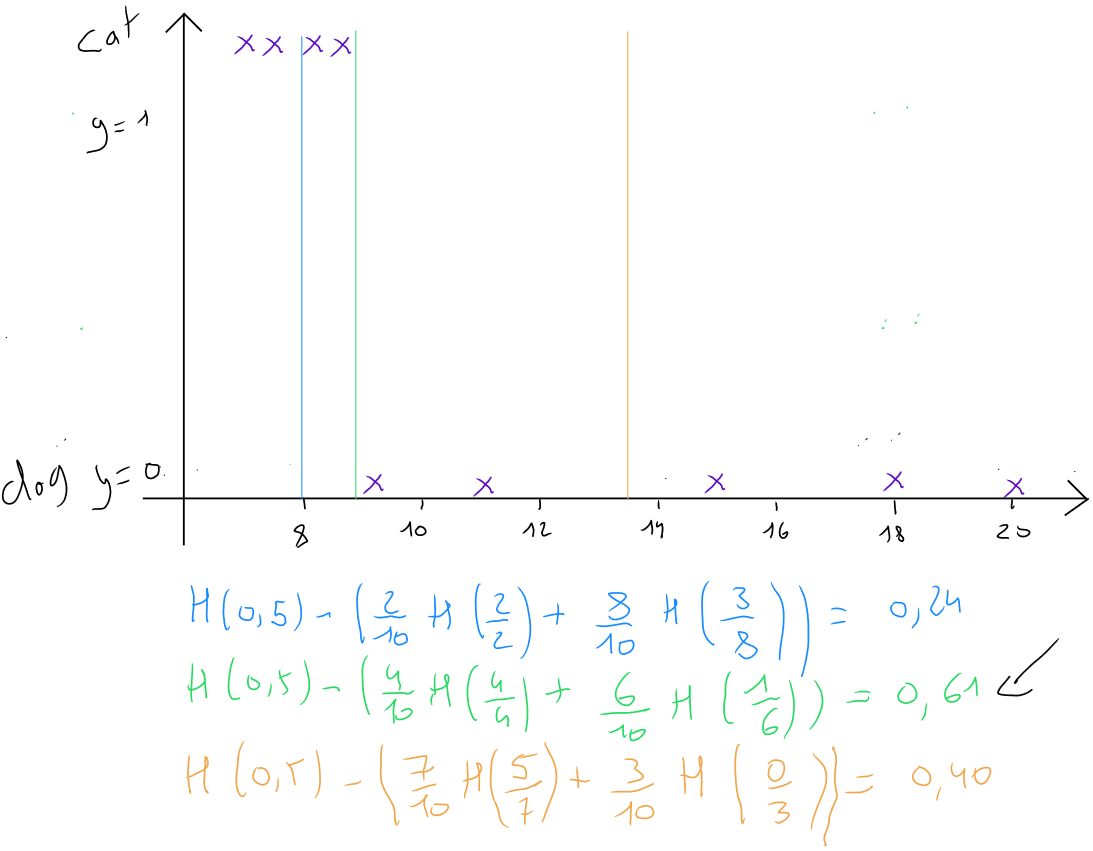
Arbre de régression

Lorsque la variable cible - la variable à prédire - est de type quantitative, nous appliquons la technique de l'arbre de régression. Prenons l'exemple suivant : nous souhaitons prédire le poids des chiens et chats sur base des prédicteurs.

Forme de l'oreille x1	Forme du visage x2	Moustache x3	Poids y
Flottante	Pas arrondie	Présente	8.8
Flottante	Arrondie	Absente	15
Pointue	Pas arrondie	Présente	9.2
Pointue	Arrondie	Présente	8.4
Pointue	Arrondie	Absente	7.6
Flottante	Pas arrondie	Absente	11
Pointue	Arrondie	Absente	10.2
Flottante	Arrondie	Absente	18
Flottante	Arrondie	Absente	20

Pour choisir les meilleures divisions d'un noeud - c'est à dire la variable qui permet de répartir de façon plus pure - l'arbre de régression ne vas plus utiliser l'entropie ( qui est utile uniquement dans le cadre d'un classement ) mais choisira la division qui réduit au mieux la variance intra-groupe.

Pour rappel, la variance est une mesure de la dispersion des valeurs d'une variable. Elle correspond à la moyenne des carrés des écarts à la moyenne et est toujours positive et s'écrit comme suit :

$\sigma^2 = \frac{\sum_{i=1}^{N} (x_i - \mu)^2}{N}$.

Soit dans le cas exemple ci-dessous, le noeud racine - root node - qui comprends tous les enregistrements à une variance de $20.51$. L'algorithme va donc tester tous les prédicteurs afin d'identifier celui qui permet de répartir les informations dans deux noeuds de décision dont la réduction de la variance sera la plus importante.

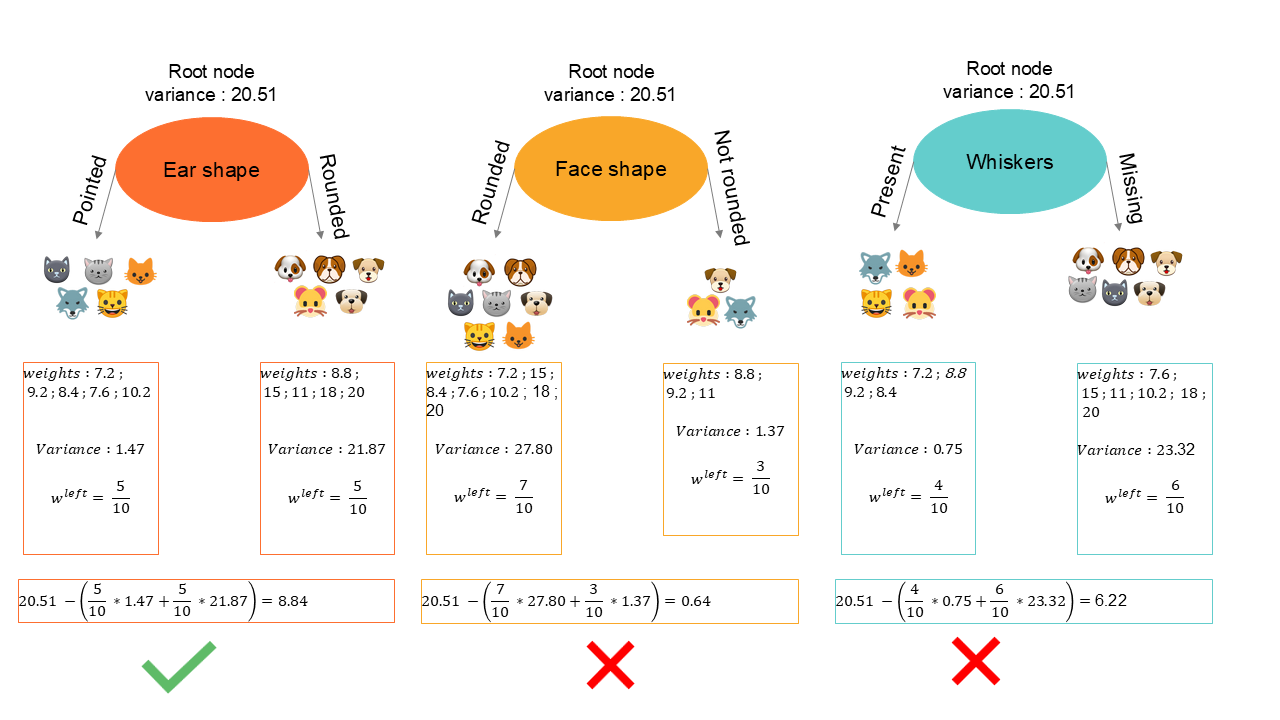
L'algorithme de l'arbre de régression va donc subdiviser chaque noeuds en de nouveaux noeuds inférieurs ( à gauche et à droite ) sur base de la réduction de la variance. La subdivision sera réalisée jusqu'à ce qu'un critère d'arrêt soit rencontré :

• Lorsque la variance d'un noeud est inférieure ou égale à un certain seuil ( estimation ) ;
• Lorsque la séparation d’un nœud excède le maximum de profondeur souhaité ;
• Lorsque le nombre d’exemples dans un nœud est inférieur à un seuil ;

La valeur finale d'un nouvel enregistrée sera prédite sur base de la moyenne des valeurs de ce noeud :

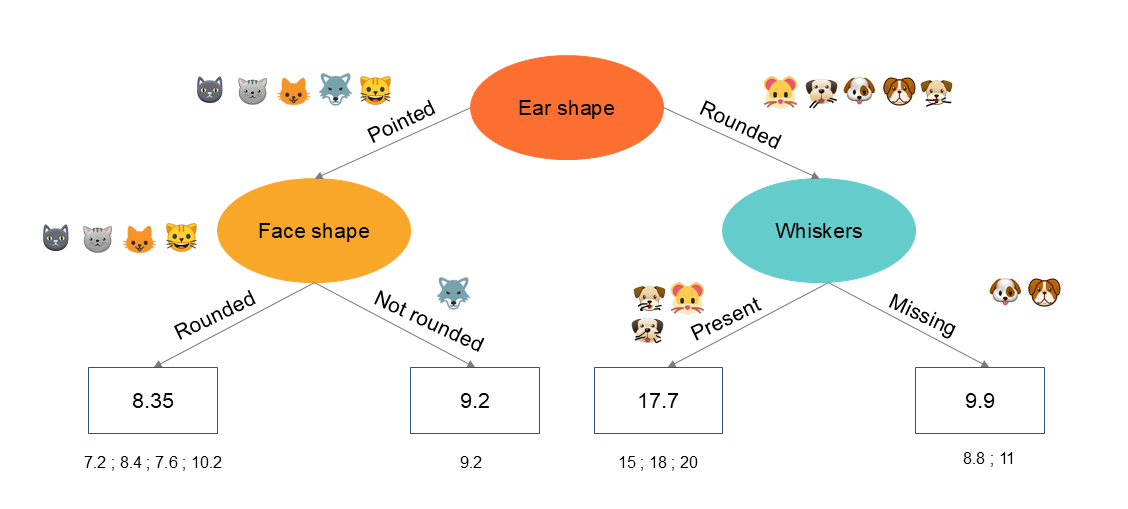
Ensemble d'arbres

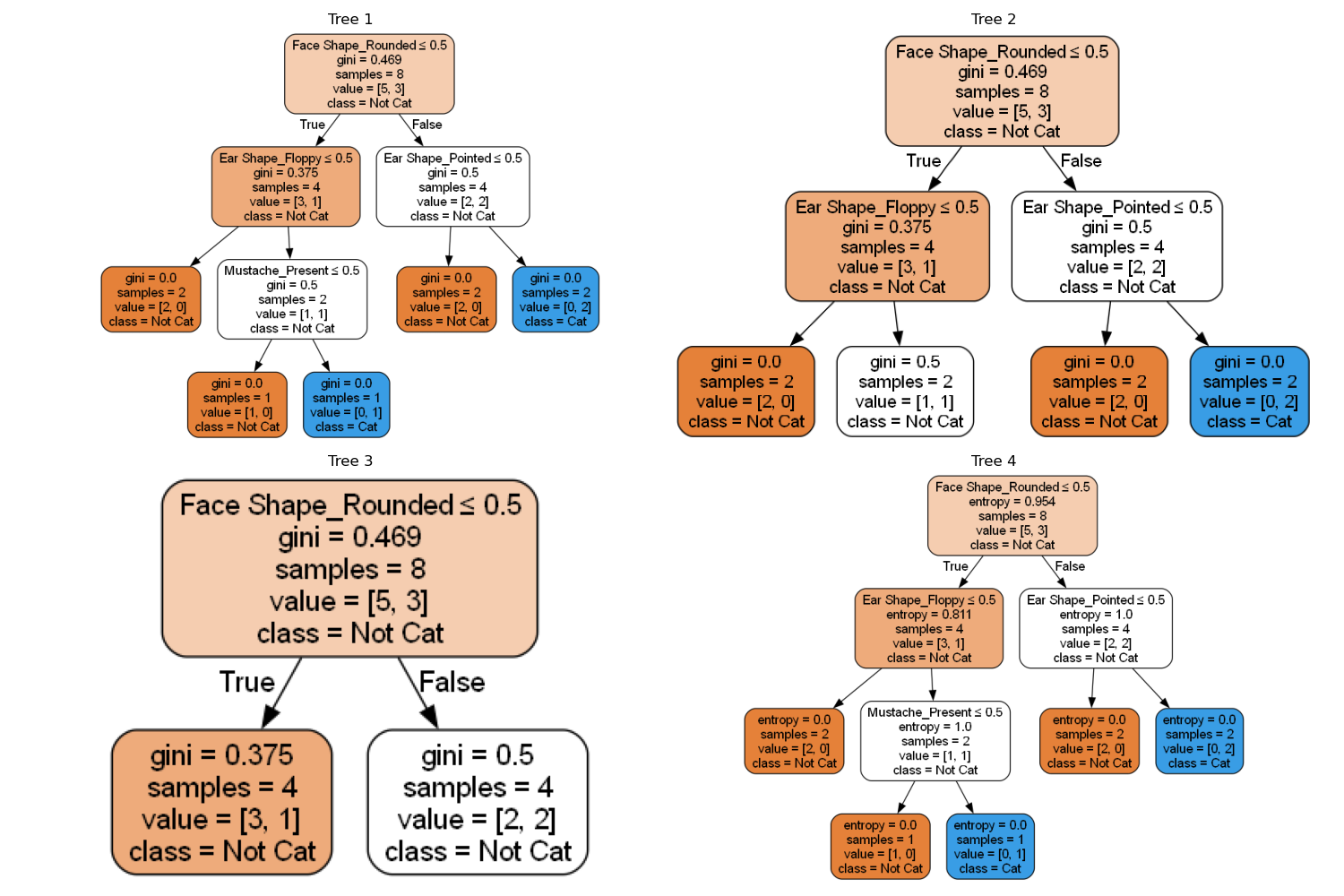
L'une des faiblesses de l'utilisation d'un seul arbre de décision est qu'il peut être très sensible à de petites modifications des données.

L'ajout de nouvelles données change considérablement la structure de l'arbre, c'est à dire la sélection des variables discriminantes par l'algorithme. En changeant une données dans le set d'apprentissage, la caractéristique présentant un gain d'information plus élevé devient la présence d'une moustache ou non au lieu de la forme de l'oreille. Par conséquent, les sous-ensembles de données obtenues dans les sous-arbres de gauche et de droite sont totalement différents.

Une solution plus robuste pour éviter ce problème consiste à construire non pas un seul arbre de décision, mais un grand nombre d'arbres de décision, ce que nous appelons un ensemble d'arbres.

Prenons le cas d'un nouvel enregistrement à prédire dans le set de données et voyons trois cas d'arbres nourris avec des données différentes :

Forme de l'oreille x1	Forme du visage x2	Moustache x3	Chat y
Pointue	Pas arrondie	Présente	?

Random Forest

Le concept des forêts aléatoires est de générer plusieurs structures d'arbres sur base de sous-ensemble de données du set d'entrainement. Nous utilisons donc plusieurs arbres qui mènent à des prédictions différentes et nous considérons la prédiction majoritaire comme étant la prédiction finale. En ayant beaucoup d'arbres de décision et en les faisant voter, l'algorithme global est moins sensible et plus robuste.

Dans le cas ci-dessous, nous utilisons trois arbres qui mènent à des prédictions différentes mais la majorité identifie l'enregistrement comme étant un chat.

La question que nous devons nous poser en tant que data scientist est de savoir comment trouver tous ces arbres de décision possibles ?

Nous appliquons une méthode d'échantillonnage aléatoire dans laquelle les éléments sont sélectionnés au hasard dans le set de données. Le sous ensemble obtenu sert à « nourrir » un premier arbre de décision. Ensuite chaque enregistrement sélectionné est remis dans l'ensemble de données avant une nouvelle sélection aléatoire d'un sous ensemble qui servira à un second arbre de décision etc.

En appliquant cette méthode, chaque échantillon aléatoire peut être différent, ce qui permet de créer plusieurs arbres différents. Ce procédé permet de réduire la variance et d'améliorer les performances de prédiction des arbres, en évitant le sur-apprentissage. En combinant les prédictions de plusieurs arbres, on obtient donc des prédictions plus robustes et plus précises.

Random Forest est un algorithme d'apprentissage supervisé qui combine plusieurs arbres de décision pour améliorer les performances de prédiction. Pour construire un modèle Random Forest, plusieurs arbres de décision sont construits à partir d'échantillons aléatoires créés à partir de l'ensemble de données d'origine en utilisant l'échantillonnage avec remplacement.

Chaque arbre de décision est entraîné sur un échantillon aléatoire différent, et utilise une sous-section aléatoire des caractéristiques disponibles pour la construction de l'arbre :

$$k < n; \quad k = \sqrt{n}$$

Random Forest est un algorithme populaire en raison de sa robustesse, de sa capacité à traiter des données avec des caractéristiques manquantes ou des valeurs aberrantes, et de sa capacité à gérer des ensembles de données de grande taille avec de nombreuses caractéristiques.

Étapes :

• $𝐹𝑜𝑟 𝑏=1 𝑡𝑜 𝐵 :$ ;
• Utilisation d'un sous-échantillonnage aléatoire pour créer un nouvel ensemble de données d'entrainement de taille $m$ et donc un nouvel arbre de décision ;
• B, selon la littérature, prends une valeur de 64 à 228. Généralement on ne dépasse pas 1000 car il a été démontré qu’un nombre de plus de 1000 arbres n’amène pas d’amélioration significative mais au contraire ralenti les calculs ;
• Chaque arbre de décision est utilisé pour effectuer une prédiction et la prédiction finale est la moyenne (pour une variable continue) ou le mode ( pour une variable catégorielle ) des prédictions de tous les arbres de décision ;

Xboost

L'algorithme Xboost est également un algorithme de forêts aléatoires. Son fonctionnement est similaire à l'algorithme random forest : plusieurs arbres de décision sont construits à partir d'échantillons aléatoires créés à partir de l'ensemble de données d'origine. Ensuite chaque enregistrement sélectionné est remis dans l'ensemble de données avant une nouvelle sélection d'un sous ensemble qui servira à un second arbre de décision.

astuce

A contrario du random forest, qui reprend un sous-ensemble de données aléatoire, l'algorithme Xboost privilégiera la probabilité de sélectionner parmi les enregistremenents, les données déjà utilisées par les arbres précédents et dont la prédiction est mauvaise

Étapes :

• $𝐹𝑜𝑟 𝑏=1 𝑡𝑜 𝐵 :$ ;
• Utilisation d'un sous-échantillonnage aléatoire pour créer un nouvel ensemble de données d'entrainement de taille $m$ et donc un nouvel arbre de décision. Au lieu de sélectionner de manière complètement aléatoire, Xboost va privilégier la probabilité de sélectionner les exemples de données qui ne sont pas correctement prédites des arbress précédemment entrainnés ;
• B, selon la littérature, prends une valeur de 64 à 228. Généralement on ne dépasse pas 100 car il a été démontrer qu’un nombre de plus de 100 arbres n’amène pas d’amélioration significative mais au contraire ralenti les calculs ;
• Chaque arbre de décision est utilisé pour effectuer une prédiction et la prédiction finale est la moyenne (pour une variable continue) ou le mode (pour une variable catégorielle) des prédictions de tous les arbres de décision ;

Code Python

Decision Tree

pip install xgboost
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from xgboost import XGBClassifier
import matplotlib.pyplot as plt
RANDOM_STATE = 55


data = pd.read_csv("data.csv")
cat_variables = ['Column_1','Column_2','Column_3','Column_4','Column_5']

df = pd.get_dummies(data = df,prefix = cat_variables,columns = cat_variables)

features = [x for x in df.columns if x not in 'NameColumnY']

X_train, X_val, y_train, y_val = train_test_split(df[features], df['NameColumnY'], train_size = 0.8, random_state = RANDOM_STATE)


min_samples_split_list = [2,10, 30, 50, 100, 200, 300, 700] ,
max_depth_list = [1,2, 3, 4,5,6, 8, 16, 32, 64, None] # None = no depth limit.

Identification of min_samples_split

accuracy_list_train = []
accuracy_list_val = []
for min_samples_split in min_samples_split_list:
    # You can fit the model at the same time you define it, because the fit function returns the fitted estimator.
    model = DecisionTreeClassifier(min_samples_split = min_samples_split,
                                   random_state = RANDOM_STATE).fit(X_train,y_train) 
    predictions_train = model.predict(X_train) ## The predicted values for the train dataset
    predictions_val = model.predict(X_val) ## The predicted values for the test dataset
    accuracy_train = accuracy_score(predictions_train,y_train)
    accuracy_val = accuracy_score(predictions_val,y_val)
    accuracy_list_train.append(accuracy_train)
    accuracy_list_val.append(accuracy_val)

plt.title('Train x Validation metrics')
plt.xlabel('min_samples_split')
plt.ylabel('accuracy')
plt.xticks(ticks = range(len(min_samples_split_list )),labels=min_samples_split_list)
plt.plot(accuracy_list_train)
plt.plot(accuracy_list_val)
plt.legend(['Train','Validation'])

Identification of max_depth

accuracy_list_train = []
accuracy_list_val = []
for max_depth in max_depth_list:
    model = DecisionTreeClassifier(max_depth = max_depth,
                                   random_state = RANDOM_STATE).fit(X_train,y_train) 
    predictions_train = model.predict(X_train) 
    predictions_val = model.predict(X_val) 
    accuracy_train = accuracy_score(predictions_train,y_train)
    accuracy_val = accuracy_score(predictions_val,y_val)
    accuracy_list_train.append(accuracy_train)
    accuracy_list_val.append(accuracy_val)

plt.title('Train x Validation metrics')
plt.xlabel('max_depth')
plt.ylabel('accuracy')
plt.xticks(ticks = range(len(max_depth_list )),labels=max_depth_list)
plt.plot(accuracy_list_train)
plt.plot(accuracy_list_val)
plt.legend(['Train','Validation'])

Run and adapt parameters

decision_tree_model = DecisionTreeClassifier(min_samples_split = 50, #Change based on chart result
                                             max_depth = 4, #Change based on chart result
                                             random_state = RANDOM_STATE).fit(X_train,y_train)
print(f"Metrics train:\n\tAccuracy score: {accuracy_score(decision_tree_model.predict(X_train),y_train):.4f}")
print(f"Metrics validation:\n\tAccuracy score: {accuracy_score(decision_tree_model.predict(X_val),y_val):.4f}")

Random Forest

pip install xgboost
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from xgboost import XGBClassifier
import matplotlib.pyplot as plt
RANDOM_STATE = 55


data = pd.read_csv("data.csv")
cat_variables = ['Column_1','Column_2','Column_3','Column_4','Column_5']

df = pd.get_dummies(data = df,prefix = cat_variables,columns = cat_variables)

features = [x for x in df.columns if x not in 'NameColumnY']

X_train, X_val, y_train, y_val = train_test_split(df[features], df['NameColumnY'], train_size = 0.8, random_state = RANDOM_STATE)

min_samples_split_list = [2,10, 30, 50, 100, 200, 300, 700]  
max_depth_list = [2, 4, 8, 16, 32, 64, None]
n_estimators_list = [10,50,100,500]

Identification of min_samples_split

accuracy_list_train = []
accuracy_list_val = []
for min_samples_split in min_samples_split_list:
    model = RandomForestClassifier(min_samples_split = min_samples_split,
                                   random_state = RANDOM_STATE).fit(X_train,y_train) 
    predictions_train = model.predict(X_train)
    predictions_val = model.predict(X_val) 
    accuracy_train = accuracy_score(predictions_train,y_train)
    accuracy_val = accuracy_score(predictions_val,y_val)
    accuracy_list_train.append(accuracy_train)
    accuracy_list_val.append(accuracy_val)

plt.title('Train x Validation metrics')
plt.xlabel('min_samples_split')
plt.ylabel('accuracy')
plt.xticks(ticks = range(len(min_samples_split_list )),labels=min_samples_split_list) 
plt.plot(accuracy_list_train)
plt.plot(accuracy_list_val)
plt.legend(['Train','Validation'])

Identification of max_depth

accuracy_list_train = []
accuracy_list_val = []
for max_depth in max_depth_list:
    model = RandomForestClassifier(max_depth = max_depth,
                                   random_state = RANDOM_STATE).fit(X_train,y_train) 
    predictions_train = model.predict(X_train) 
    predictions_val = model.predict(X_val) 
    accuracy_train = accuracy_score(predictions_train,y_train)
    accuracy_val = accuracy_score(predictions_val,y_val)
    accuracy_list_train.append(accuracy_train)
    accuracy_list_val.append(accuracy_val)

plt.title('Train x Validation metrics')
plt.xlabel('max_depth')
plt.ylabel('accuracy')
plt.xticks(ticks = range(len(max_depth_list )),labels=max_depth_list)
plt.plot(accuracy_list_train)
plt.plot(accuracy_list_val)
plt.legend(['Train','Validation'])

Identification of n_estimators

accuracy_list_train = []
accuracy_list_val = []
for n_estimators in n_estimators_list:
    model = RandomForestClassifier(n_estimators = n_estimators,
                                   random_state = RANDOM_STATE).fit(X_train,y_train) 
    predictions_train = model.predict(X_train) 
    predictions_val = model.predict(X_val) 
    accuracy_train = accuracy_score(predictions_train,y_train)
    accuracy_val = accuracy_score(predictions_val,y_val)
    accuracy_list_train.append(accuracy_train)
    accuracy_list_val.append(accuracy_val)

plt.title('Train x Validation metrics')
plt.xlabel('n_estimators')
plt.ylabel('accuracy')
plt.xticks(ticks = range(len(n_estimators_list )),labels=n_estimators_list)
plt.plot(accuracy_list_train)
plt.plot(accuracy_list_val)
plt.legend(['Train','Validation'])

Run and adapt parameters

random_forest_model = RandomForestClassifier(n_estimators = 100,
                                             max_depth = 16, 
                                             min_samples_split = 10).fit(X_train,y_train)

print(f"Metrics train:\n\tAccuracy score: {accuracy_score(random_forest_model.predict(X_train),y_train):.4f}\nMetrics test:\n\tAccuracy score: {accuracy_score(random_forest_model.predict(X_val),y_val):.4f}")

Xboost

pip install xgboost
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from xgboost import XGBClassifier
import matplotlib.pyplot as plt
RANDOM_STATE = 55


data = pd.read_csv("data.csv")
cat_variables = ['Column_1','Column_2','Column_3','Column_4','Column_5']

df = pd.get_dummies(data = df,prefix = cat_variables,columns = cat_variables)

features = [x for x in df.columns if x not in 'NameColumnY']



X_train, X_val, y_train, y_val = train_test_split(df[features], df['NameColumnY'], train_size = 0.8, random_state = RANDOM_STATE)

n = int(len(X_train)*0.8) 

X_train_fit, X_train_eval, y_train_fit, y_train_eval = X_train[:n], X_train[n:], y_train[:n], y_train[n:]

min_samples_split_list = [2,10, 30, 50, 100, 200, 300, 700]  
max_depth_list = [2, 4, 8, 16, 32, 64, None]
n_estimators_list = [10,50,100,500]

Identification of min_samples_split

accuracy_list_train = []
accuracy_list_val = []
for min_samples_split in min_samples_split_list:
    model = RandomForestClassifier(min_samples_split = min_samples_split,
                                   random_state = RANDOM_STATE).fit(X_train,y_train) 
    predictions_train = model.predict(X_train)
    predictions_val = model.predict(X_val) 
    accuracy_train = accuracy_score(predictions_train,y_train)
    accuracy_val = accuracy_score(predictions_val,y_val)
    accuracy_list_train.append(accuracy_train)
    accuracy_list_val.append(accuracy_val)

plt.title('Train x Validation metrics')
plt.xlabel('min_samples_split')
plt.ylabel('accuracy')
plt.xticks(ticks = range(len(min_samples_split_list )),labels=min_samples_split_list) 
plt.plot(accuracy_list_train)
plt.plot(accuracy_list_val)
plt.legend(['Train','Validation'])

Identification of max_depth

accuracy_list_train = []
accuracy_list_val = []
for max_depth in max_depth_list:
    model = RandomForestClassifier(max_depth = max_depth,
                                   random_state = RANDOM_STATE).fit(X_train,y_train) 
    predictions_train = model.predict(X_train) 
    predictions_val = model.predict(X_val) 
    accuracy_train = accuracy_score(predictions_train,y_train)
    accuracy_val = accuracy_score(predictions_val,y_val)
    accuracy_list_train.append(accuracy_train)
    accuracy_list_val.append(accuracy_val)

plt.title('Train x Validation metrics')
plt.xlabel('max_depth')
plt.ylabel('accuracy')
plt.xticks(ticks = range(len(max_depth_list )),labels=max_depth_list)
plt.plot(accuracy_list_train)
plt.plot(accuracy_list_val)
plt.legend(['Train','Validation'])

Identification of n_estimators

accuracy_list_train = []
accuracy_list_val = []
for n_estimators in n_estimators_list:
    model = RandomForestClassifier(n_estimators = n_estimators,
                                   random_state = RANDOM_STATE).fit(X_train,y_train) 
    predictions_train = model.predict(X_train) 
    predictions_val = model.predict(X_val) 
    accuracy_train = accuracy_score(predictions_train,y_train)
    accuracy_val = accuracy_score(predictions_val,y_val)
    accuracy_list_train.append(accuracy_train)
    accuracy_list_val.append(accuracy_val)

plt.title('Train x Validation metrics')
plt.xlabel('n_estimators')
plt.ylabel('accuracy')
plt.xticks(ticks = range(len(n_estimators_list )),labels=n_estimators_list)
plt.plot(accuracy_list_train)
plt.plot(accuracy_list_val)
plt.legend(['Train','Validation'])

Run and adapt parameters

xgb_model = XGBClassifier(n_estimators = 500, learning_rate = 0.1,verbosity = 1, random_state = RANDOM_STATE)
xgb_model.fit(X_train_fit,y_train_fit, eval_set = [(X_train_eval,y_train_eval)], early_stopping_rounds = 10)
xgb_model.best_iteration
# Change early_stopping_rounds based on best_iteration

print(f"Metrics train:\n\tAccuracy score: {accuracy_score(xgb_model.predict(X_train),y_train):.4f}\nMetrics validation:\n\tAccuracy score: {accuracy_score(xgb_model.predict(X_val),y_val):.4f}")