Réseau de neurones

L'idée du réseau de neurones informatique - neural network - est de s'inspirer du fonctionnement d'un cerveau humain. Il s'agit d'une technique statistique conceptualisée fin des années 50 dans le cadre d'un algorithme d'apprentissage supervisé de classement binaire, et qui a connu diverses évolutions dans les années suivantes ( modèle de réseau de neurones récurrents, le perceptron à multicouche,...).

Le réseau de neurones est une technique fortement utilisée fin des années $80$ et début des années $90$ de par sa particularité de pouvoir utiliser entre autre des données non-structurées - à ce moment-là, la reconnaissance manuscrite ; Son utilité a été démontrée à cette époque-là, dans le tri de courrier des services postaux et l'identification des symboles monétaires sur les chèques.

Malgré ses prouesses dans la matière, ce n'est qu'à partir des années 2000 à 2010, que cette technique - rebaptisée Deep learning - a ressurgit et démontré de hautes capacités dans des concepts révolutionnaires tels que la reconnaissance d'images ou la reconnaissance vocale. Cette résurgence est liée entre autre à deux facteurs : d'une part, l'évolution hardware et la capacité des ordinateurs à atteindre des performances considérables grâce notamment à l'utilisation de GPU (Graphic Process Unit) - particulièrement puissant pour les calculs vectoriels - et, d'autre part, également par l'accessibilité à des quantités de données de plus en plus importantes. Les chercheurs dans le domaine se sont en effet rendu compte qu'au plus ils nourrissaient un modèle de données, et au plus, ils définissaient une architecture large grâce aux capacités de calcul, au plus les performances étaient considérables.

L'appellation Deep learning ( apprentissage profond ) - apparue autour de l'année 2005 - est principalement liée à la particularité du fonctionnement de l'architecture des réseaux de neurones ; la « boite noire des couches cachées ».

Pour comprendre un réseau de neurones informatique, il est important de comprendre les fondements d'un réseau de neurones biologique.

remarque

Certains schémas et concepts présentés ici sont inspirés du cours Machine Learning d'Andrew Ng, programme créé en collaboration entre Stanford university Online Education et DeepLearning.AI disponible sur Coursera. Retrouvez le cours original ici : Machine Learning by Andrew Ng.

Représentation d'un neurone :

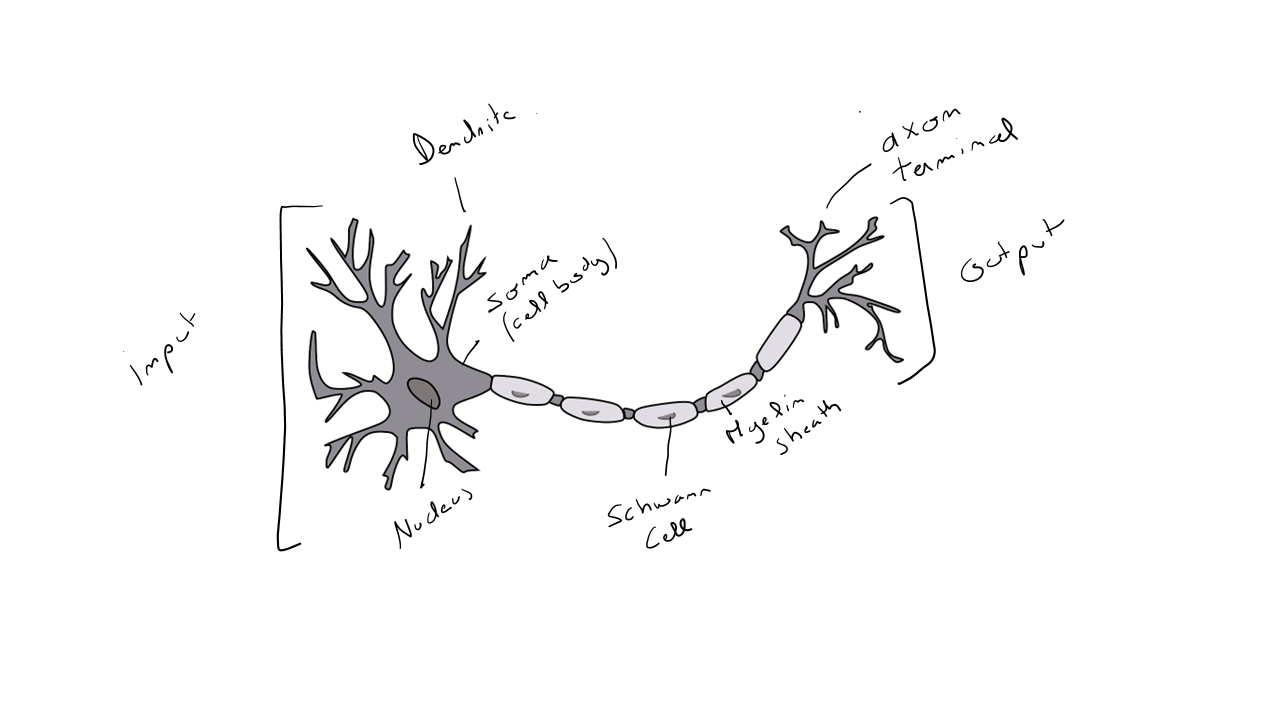
Représentation d'un neurone informatique :

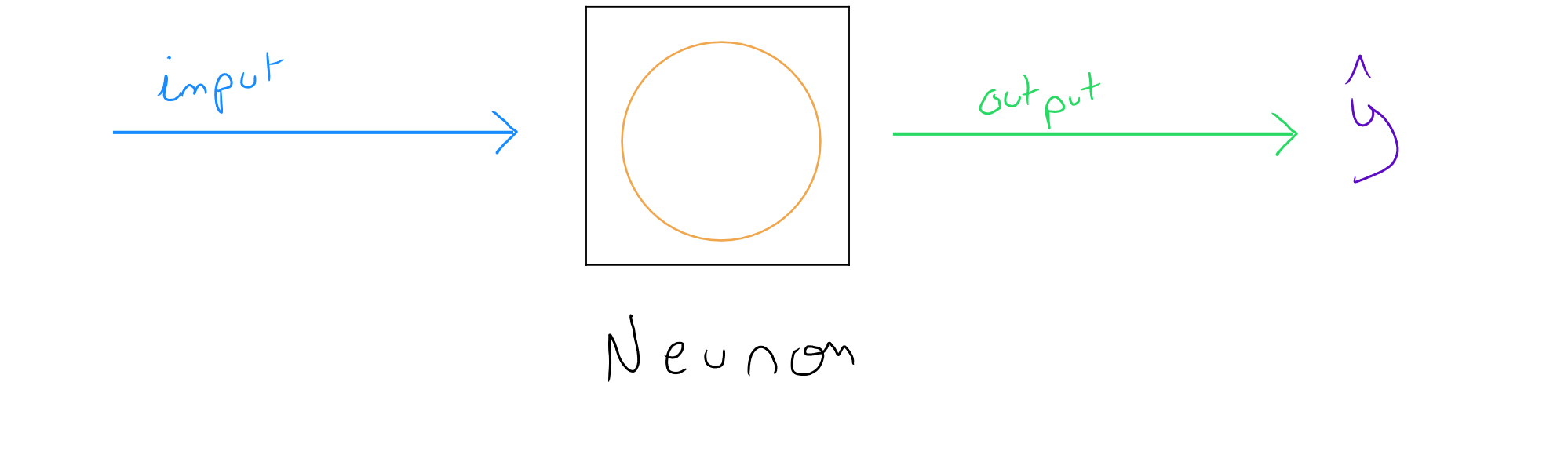
Un humain possède environs $86$ à $100$ milliards de neurones dans son cerveau. Le rôle d'un neurone - cellule du cerveau - est de transmettre des informations et permettre les activités motrices et cognitives. Concrètement, si au tournant d'un coin de rue, nous nous retrouvons face à un lion échappé d'un zoo, nos neurones vont agir : identification et compréhension du danger ; association avec des nombreuses informations de la situation et des possibilités de recours ; accélération cardiaque pour augmenter le flux sanguin vers les membres et préparer une éventuelle fuite motrice ( malgré qu'il est recommandé de ne pas bouger ! ) etc.

Les neurones communiquent entre eux par des signaux électriques ( influx nerveux ) et sont connectés de part et d'autre grâce aux dendrites et axones. Un neurone reçoit donc une information d'un autre neurone par signal électrique en entrée via les dendrites. Le signal se propage le long de l'axone du neurone pour être renvoyé ensuite à un autre neurone qui s'activera à son tour. Les axones sont composés d'une gaine myéline dans le but d'accélérer la conduction de l'influx nerveux et au plus la fréquence du signal électrique est importante, au plus le neurone va produire des substances chimiques, à savoir les neurotransmetteurs qui permettent la transmission d'information aux autres neurones par les synapses. L'environnement des neurones, dans le système nerveux, est composé de cellule gliales ( 50 % du volume cérébral ) dont le rôle est d'apporter des nutriments et de l'oxygène mais également d'éliminer les cellules mortes.

L'Homme ( avec un grand H ) s'est toujours inspiré de la nature pour de nombreuses évolutions. Nous verrons par la suite la puissance de cette technique statistique, mais il est fondamental de mettre en évidence une chose importante : si nous voulons être capable de créer des intelligences artificielles aussi fortes que celle de l'homme - ( et notons que l'intelligence prend des formes variées telles que la logique, la conscience de soi, l'apprentissage, la créativité, l'émotion,...) - nous devrions être capable de comprendre parfaitement le fonctionnement d'un cerveau humain, ce qui n'est pas encore entièrement le cas. Par exemple, les dernières recherches mettent de plus en plus en évidence les rôles importants - non reproductibles d'un point de vue informatique - des cellules gliales et de la myéline.

Toutefois, si nous nous référons au fonctionnement basique d'un neurone, il pourrait être vulgarisé comme suit : une couche d'entrée reçoit une ou plusieurs informations via les dendrites sous forme de flux électrique ; les flux électriques sont activés dans une certaine densité à travers l'axone pour produire une information de sortie ( flux électrique ) qui servira d'information d'entrée à un autre neurone.

Il est intéressant de faire le parallèle avec le fonction d'un ordinateur qui en réalité est composé de nombreux transistors orchestrés via le Central Processing Unit ( CPU ) et dont le rôle est de contrôler l'intensité d'un signal électrique permettant d'utiliser trois opérateurs : AND, OR et NOT. Ces conditions sont représentées par le passage d’un courant électrique ou le blocage de ce courant qui est au final exprimé en tant que 1 ou 0.

Réseau de Neurones & Régression linéaire/logistique

Le processus d'un réseau de neurone informatique est également relativement simpliste, à savoir : nous avons une ou des données en entrée, cette donnée ou ces données sont traité(es) dans une couche sur base de fonctions d'activation et nous obtenons en sortie une valeur.

En appliquant un zoom sur un neurone informatique, nous découvrons qu'une régression logistique ou une régression linéaire ( selon la fonction d'activation ) est en réalité un modèle simplifié d'un neurone :

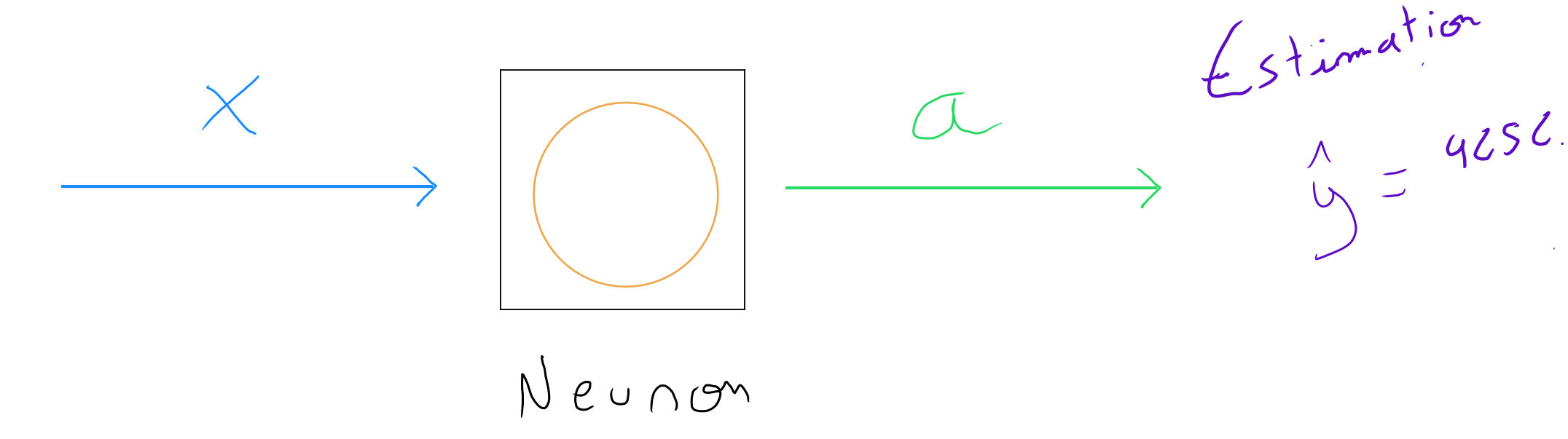
$x$ = valeurs de la variable explicative ( prédicteur )

$a$ = fonction d'activation ( mesure d'élévation de la valeur de sortie ) $= f(z) =  \frac{1}{1 + e^{(-(w *x + b))}}$ = probabilité ou $\hat{Y} = b + w * x$ estimation

astuce

Un réseau de neurones informatique pourrait être considéré comme étant le réseau d'un ensemble de régressions linéaires et/ou logistiques ; les techniques étant définies sur base d'une fonction d'activation par couche (Linéaire, Logistique, Tahn, ReLu, Softmax).

Pour illustrer le fonctionnement d'un réseau de neurones, prenons le cas de la prédiction suivante : un commerçant qui vend des chaussures fait appel à nos services et aimerait que nous l'aidions à prédire si un nouveau modèle de sneakers sera une top ventes ou non afin de s'assurer une gestion des stocks optimale et également savoir s'il doit inclure ces sneakers dans son folder publicitaire du prochain mois.

$\hat{y}$ correspond donc à Top ventes $( 1 )$ ou pas Top ventes $( 0 )$. Il s'agit donc d'une technique supervisée de classement. Si nous disposons d'un seul prédicteur $x =$ prix ; Nous pourrions définir que le meilleur modèle à utiliser est une régression logistique simple et nous pourrions faire le rapprochement suivant entre un neurone ( une unité d'un réseau de neurones ) et notre régression logistique :

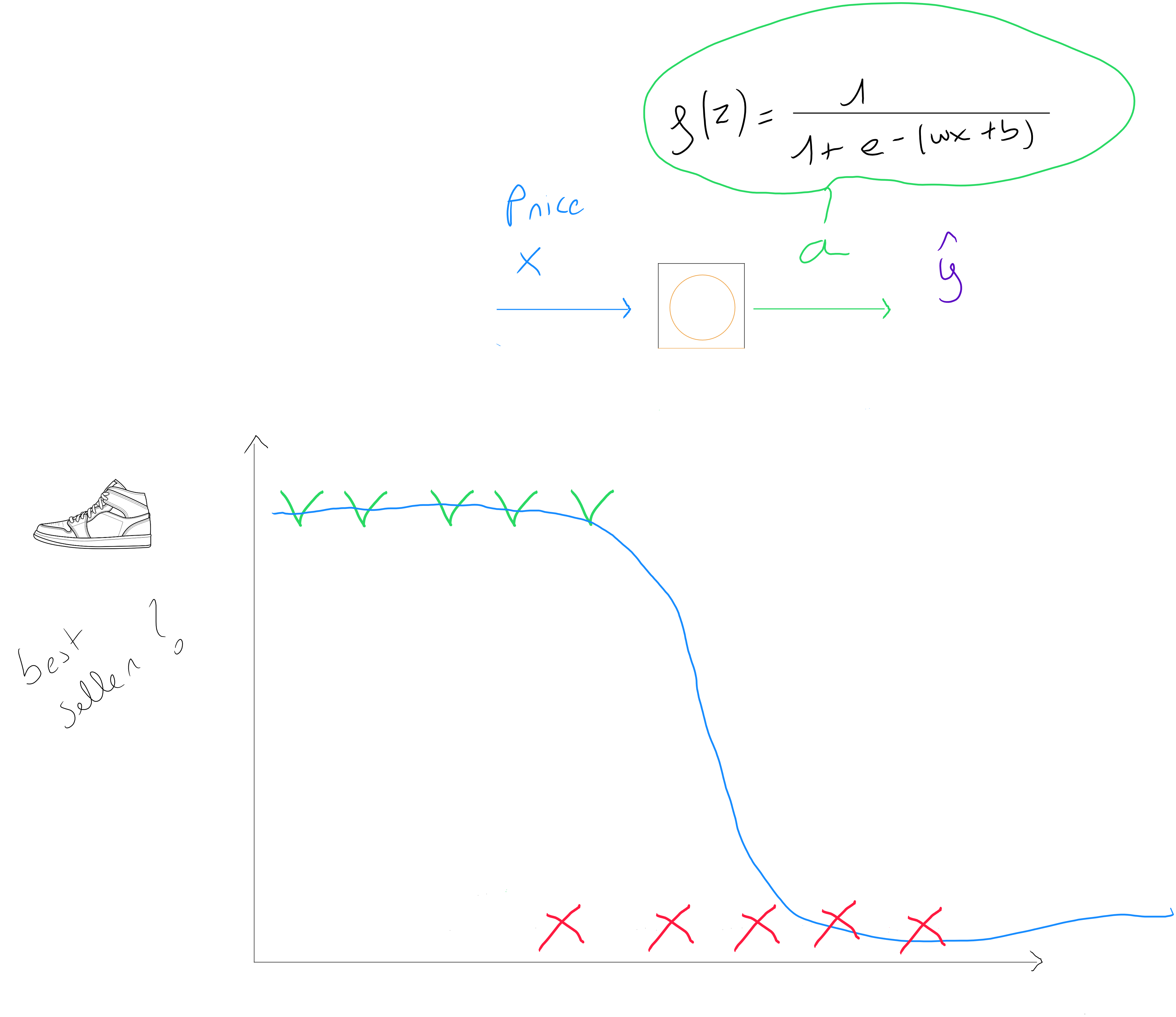
Dans le cas où nous aurions de nombreux prédicteurs, nous appliquerions la fonction suivante de la régression logistique à prédicteurs multiples : $f(z) = \frac{1}{1 + e^{(-(\vec{w} \cdot \vec{x} + b))}}$. Concrètement, cela signifie qu'un réseau de neurones va estimer des valeurs de paramètres $w$ et $b$ pour chaque neurones de chaque couche du réseau.

Si nous décidons d'utiliser un réseau de neurones et que nous disposons de plusieurs prédicteurs :

Prix	Coût livraison	Frais marketing	Matière (qualité)	Top Seller
80 €	5 €	10 €	9	1
50 €	2 €	8 €	6	0
120 €	8 €	15 €	9	1
65 €	3 €	6 €	4	0
...	...	...	...	...
95 €	7 €	12 €	3	1

Architecture d'un réseau de neurones

La particularité d'un réseau de neurones - son architecture -, c'est que l'on va disposer de ce que l'on appelle une couche d'entrée, d'une ou plusieurs couches cachées et d'une couche de sortie. La couche d'entrée et la couche de sortie sont visibles car il s'agit respectivement des valeurs des prédicteurs $\vec{x}$ et de la variable prédite $\hat{y}$.

Il est par contre impossible en tant que data scientist de savoir ce qui se passe dans une couche cachée. On appelle cela « la boîte noire ». Il ne s'agit aucunement d'une intelligence quelconque de la machine qui - nous l'abordons plus loin - définit les couches cachées en fonctionnant par rétropropagation du gradient de l'erreur.

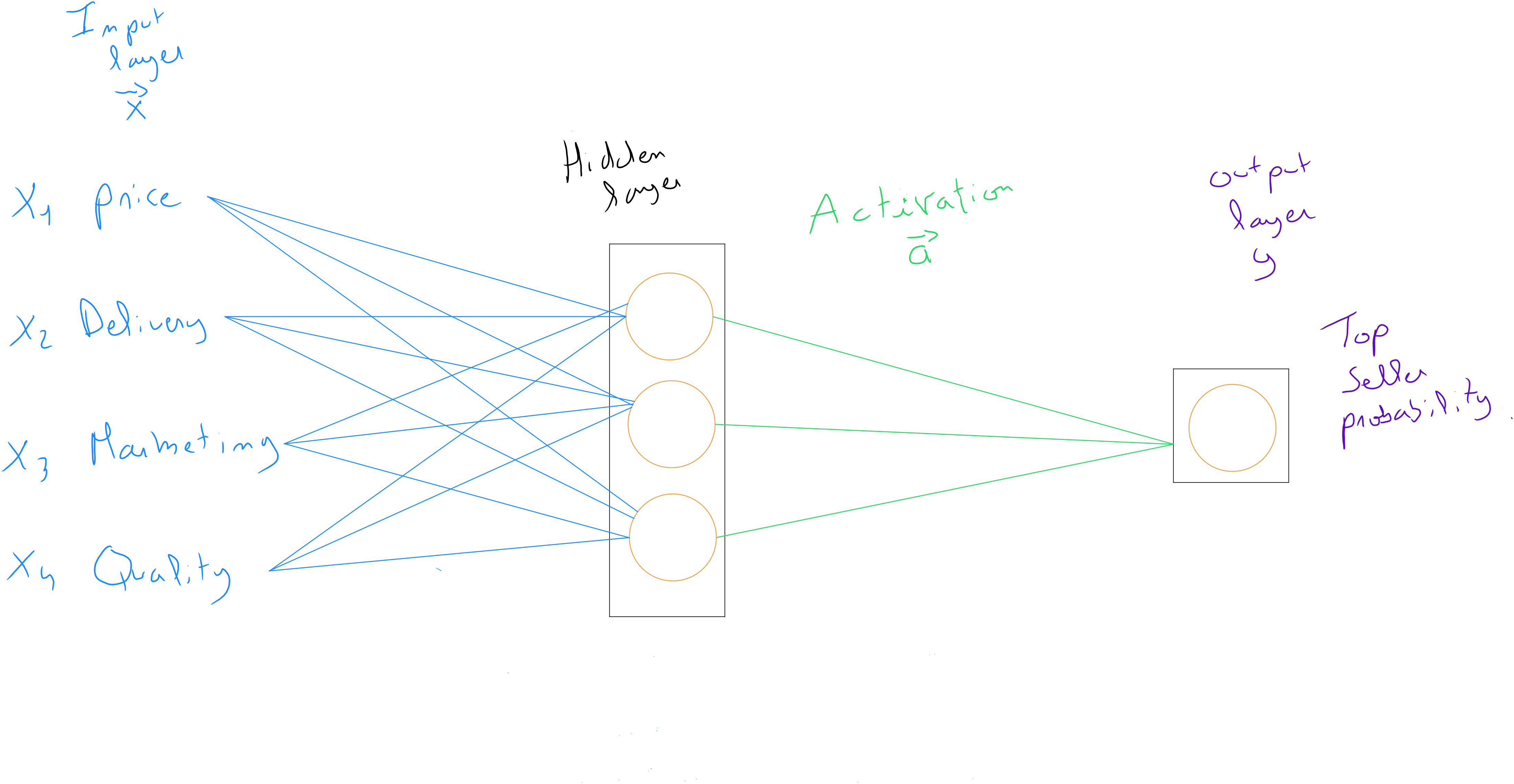
Bien que toutes les valeurs des $x$ soient utilisées comme valeurs d'entrée dans chaque neurone de la couche cachées dans l'exemple ci-dessus, il est important de tenir compte du fait que dans le cadre de son apprentissage, le modèle peut potentiellement annuler des variables ou réduire l'impact de certaines variables sur base de la définition des poids $w$.

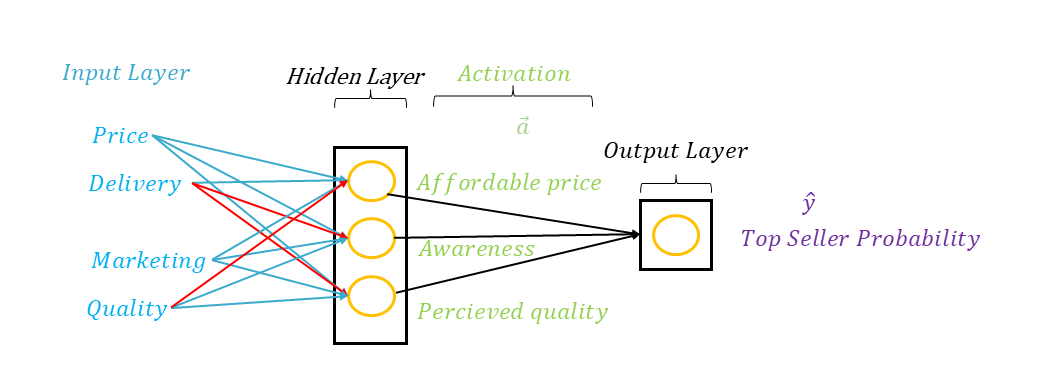
Si nous avions accès dans notre exemple à la manière dont le modèle procède dans la couche cachée, nous découvririons peut-être qu'il utilise et regroupe les variables d'entrées selon trois critères ( $3$ neurones ), à savoir : le prix abordable, la notoriété et la qualité perçue. Pour la notoriété, bien que le neurone reçoit les informations des coûts de livraison, ces derniers n'ont peut-être pas d'incidence réelle sur la notoriété et sont quasi annulés par le poids ; alors que le prix et les effort marketing ont un impact conséquent. Et finalement que les valeurs de ces trois neurones sont réutilisées en entrée pour le dernier neurone qui sur base de ces informations définit la probabilité d'être un top ventes.

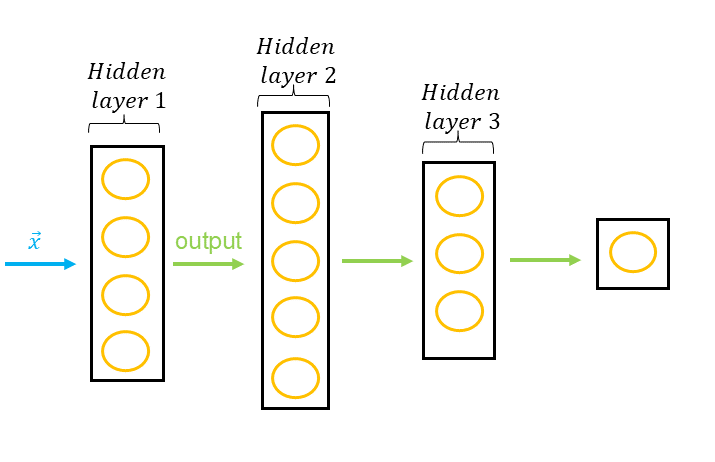
Un réseau de neurones peut avoir de nombreuses couches cachées, on parle alors d'un MLP pour Multi-Layer Perceptron. En tant que data scientist, nous devons d'ailleurs prendre une décision importante : celle d'initier différentes architectures de réseaux de neurones qui seront évaluées pour pouvoir identifier la plus efficiente.

Un réseau de neurones peut être utilisé pour faire un classement ou une estimation, et demande comme prédicteurs, des variables quantitatives ou des variables qualitatives qui ont été transformées soit dans le cadre d'un encodage one-hot soit par le processus de numérisation de variables discrètes. Pour assurer une certain efficience, les données doivent être normalisées avant d'être séparées dans un set d'entrainement et un set de validation.

En tant que data scientist, nous devons définir l'architecture de notre réseau de neurones, c'est à dire le nombre de couches cachées et le nombre de neurones par couches. En réalité, plusieurs architectures sont évaluées. Par exemple, si nous avons $8$ variables $x$, nous pourrions définir trois architectures comme suit :

• Input layer = 8 ; Layer_1 = 16 ; Layer_2 = 32 ; Layer_3 = 16 ; output layer = 1
• Input layer = 8 ; Layer_1 = 32 ; Layer_2 = 16 ; output layer = 1
• Input layer = 8 ; Layer_1 = 64 ; Layer_2 = 32 ; Layer_3 = 16 ; Layer_4 = 4 ; output layer = 1

Et même éventuellement tester pour ces trois architectures, des fonctions d'activation différentes entre les couches ( logistic, linear , relu, tahn - voir section fonctions d'activation - ) ainsi que différents taux d'apprentissage et différentes tailles de batch (découpage de sous-ensemble de données pour la mise à jour des paramètres).

Chaque configuration sera lancée et entrainée et le modèle final présentant la meilleure efficience sera sélectionné.

Construction d'une couche

Comme nous l'avons abordé précédemment, une couche - un layer - regroupe un ensemble de neurones et chaque neurone peut être considéré comme étant une régression linéaire et/ou logistique selon la fonction d'activation. En tant que data scientist, nous devons donc identifier l'architecture la plus performante, ce qui signifie le nombre de couche et, par couche, le nombre de neurones.

La différence entre une régression logistique/linéaire et un neurone est que la valeur finale obtenue par un neurone - l'output - est considéré comme la résultat de la fonction d'activation ( qui est égale à la fonction logistique ou linéaire ( des dérivées Tahn, ReLu ou Softmax)).

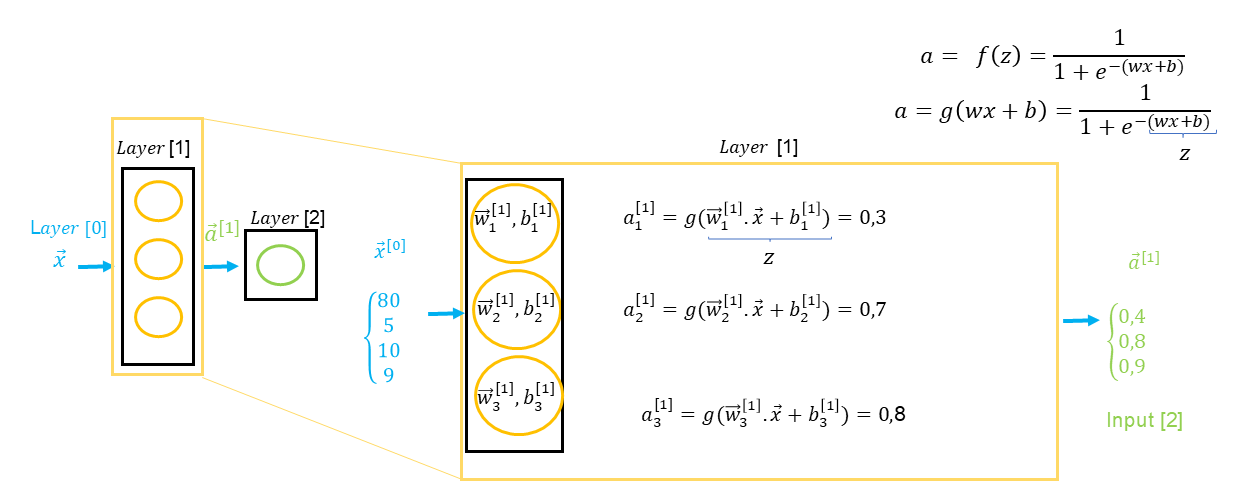
Le résultat de la couche $2$ est un vecteur $a$ comprenant chacune des valeurs sortante de chaque neurone. Dans notre exemple ci-dessus, nous constatons que l'input layer correspond à un vecteur $x$ ( $\vec{x}$ ), c'est à dire des valeurs pour chaque prédicteur ( prix $X_1$, frais de livraison $X_2$, coûts marketing $X_3$ et qualité $X_4$ ). Le résultat correspond à un vecteur $a$ ( $\vec{a}$ ) reprenant des valeurs sortantes de chaque neurone à savoir $a_1^{[1]},a_2^{[1]},a_3^{[1]}$, qui à leur tour deviendront des valeurs d'entrée pour la prochaine couche et ainsi de suite jusqu'à la couche finale.

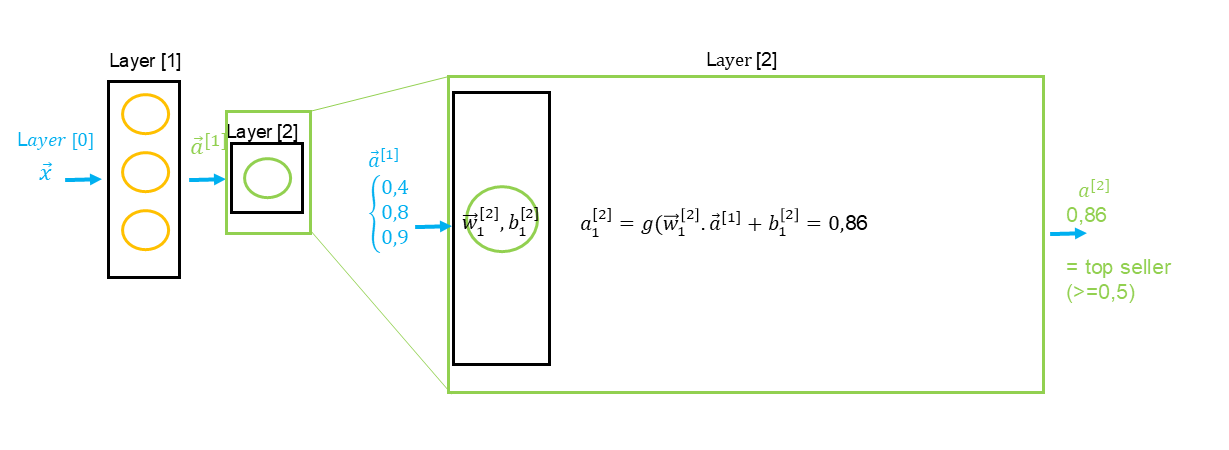
Si nous avons une seconde couche cachée, il est important de considérer la particularité des annotations de la formule en ce qui concerne les données entrantes qui proviennent de la couche précédente : $g(z) = g(\vec{w} \cdot \textcolor{red}{\vec{a^{[Layer -1]}}} + b)$.

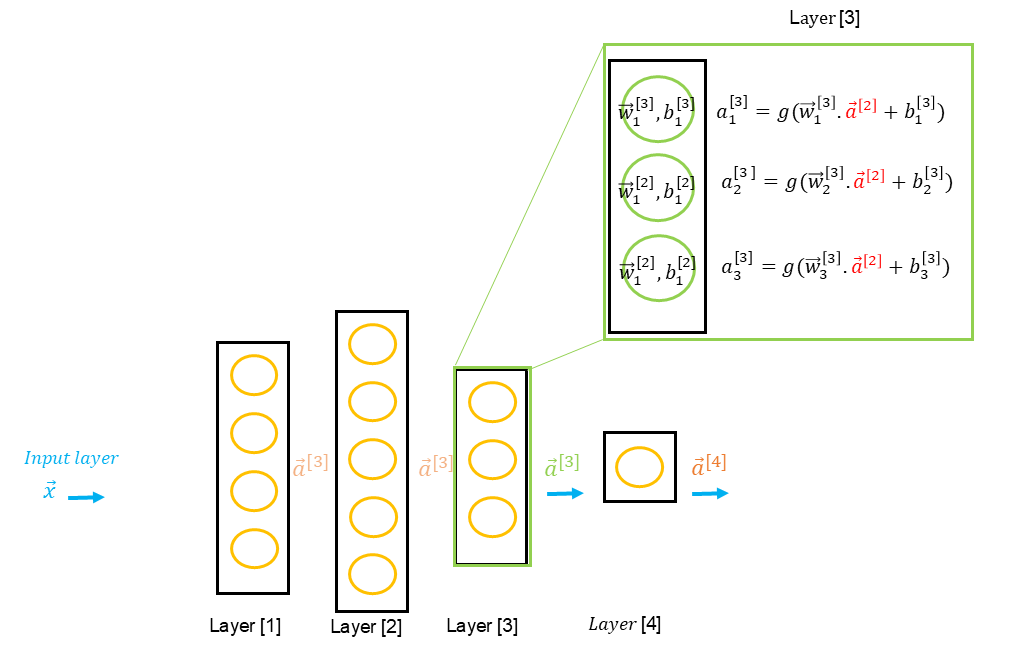
Propagation avant

La propagation en avant ( en anglais forward propagation ) est l'étape initiale de la mise en oeuvre de la création d'un modèle de réseau de neurones. Rappelons-nous que toutes les étapes de préparation des données ainsi que la définition de l'architecture du réseau de neurones concerne l'algorithme. Lorsque ces étapes sont prêtes, il est temps lancer le modèle. La modèle étant l'application de l'algorithme sur des données et l'évaluation de l'ensemble du processus.

On parle de propagation vers l'avant étant donné que les données sont propagées vers l'avant depuis l'input layer ( couche d'entrée ), en passant par les hiddent layers ( couches cachées ) pour enfin arriver à l'output layer, le résultat final. Chaque layer comprend un ensemble de neurones ( chaque unité étant une sorte de régression linéaire ou logistique ) et des fonctions d'activation sont définies pour chaque couche. En général, on utilise la même fonction d'activation pour les couches cachées et la même fonction ou une fonction différente pour la couche de sortie.

En conséquence, la propagation avant consiste à propager les données à travers les différentes couches qui définissent une valeur à chaque sortie sur base d'une fonction d'activation, jusqu'à la prédiction finale.

Bien entendu, nous avons vu dans le cadre de la régression linéaire et logistique que l'objectif d'un algorithme supervisé est de prédire des valeurs sur base d'une fonction coût et de l'application d'un algorithme d'optimisation pour minimiser ce coût en identifiant les valeurs des paramètres $w$ et $b$. Le réseau de neurones fonctionne exactement de la même manière car il s'agit d'une technique paramétrique, et comme lors de l'initiation d'une régression linéaire ou logistique, des valeurs aléatoires sont définies pour les paramètres $w$ et $b$ lors de la première itération ; dans ce cas-ci lors de la propagation avant.

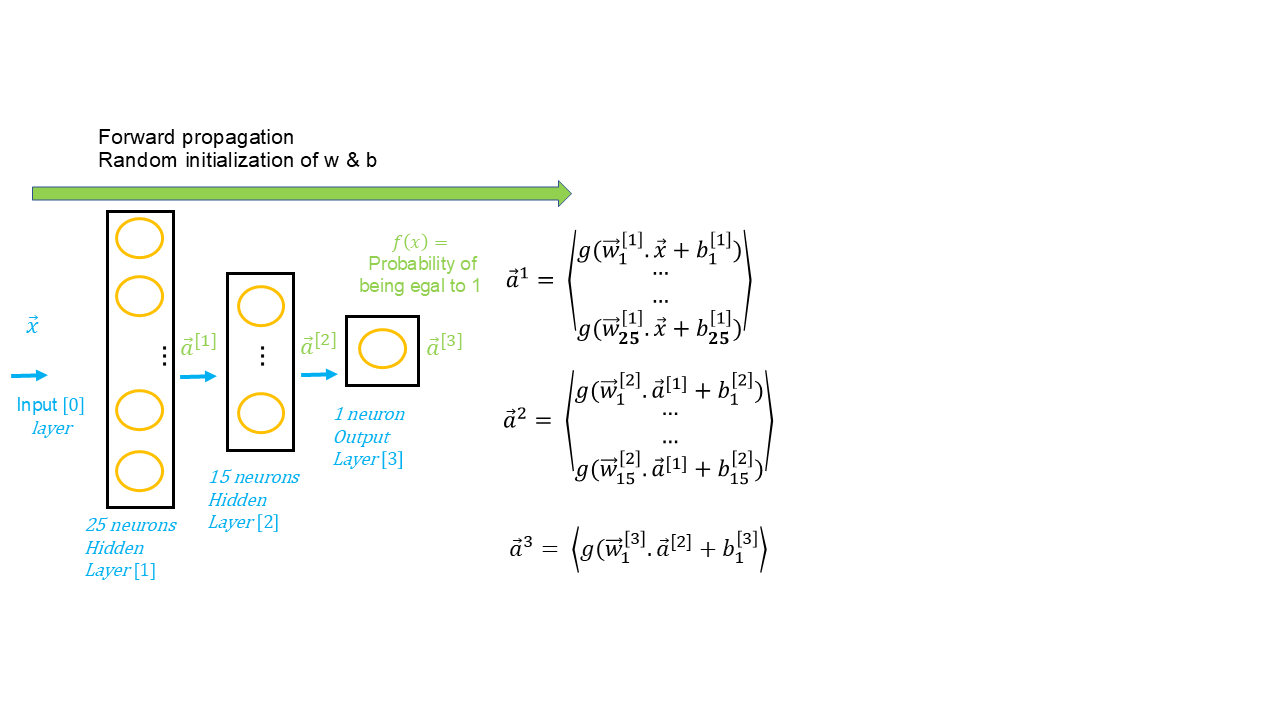
Propagation arrière

Lorsque les prédictions ont été réalisées grâce à la propagation avant et l'initialisation aléatoire des paramètres $w$ et $b$, l'algorithme d'un réseau de neurones intègre également le concept de fonction coût et va également utiliser un algorithme afin de pouvoir minimiser la fonction de coût appliquée en trouvant l'optimal local, c'est à dire identifier les valeurs de $w$ et $b$ qui minimisent les différences entre les valeurs prédites et les valeurs réelles.

La propagation arrière consiste donc à repartir dans les différentes couches du réseau de neurones, mais cette fois-ci dans le sens inverse afin de réadapter l'ensemble des valeurs de $w$ et $b$ de chaque neurones de chaque couche. Dans le schéma ci-dessous, nous découvrons en bleu la direction de la propagation avant et en rouge la rétropropagation.

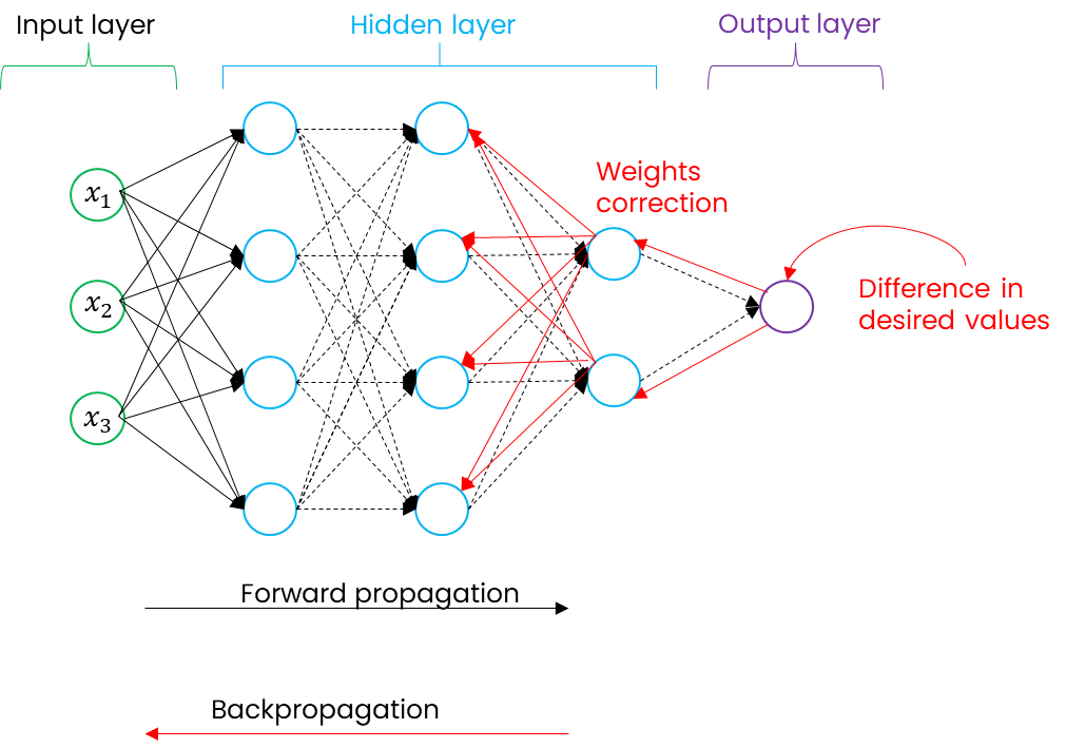
Fonction coût

Nous avons vu qu'un réseau de neurones est similaire - pour chaque neurone en tant que unité - à une régression linéaire et/ou une régression logistique. Dans la première étape, nous appliquons la propagation avant, c'est à dire l'application de l'algorithme à nos données sur base de paramètres initiés de manière aléatoire.

En conséquence, nous aurons des différences fondamentales entre les valeurs réelles et connues du set d'entrainement et les valeurs prédites de notre première itération ( epoch ). Pour pouvoir identifier ces erreurs, un réseau de neurones utilise pour chaque neurone ( chaque neurone ayant un paramètre $b$ et un paramètre $w$ associés ) une fonction de coût qui est identique à la régression linéaire pour un réseau de neurones d'estimation et à la régression logistique pour un réseau de neurones de classement, à savoir :

Pour la régression linéaire

$$J(w, b) = \frac{1}{2m} \sum_{i=1}^n ((w \cdot x^{(i)} + b) - y^{(i)})^2$$

Pour la régression logistique

$$J(\vec{w}, b) = -\frac{1}{m} \sum_{i=1}^n y^{(i)}log(f(\vec{w},b)\vec{x}^{(i)}) + (1-y^{(i)})log(1-f(\vec{w},b)\vec{x}^{(i)})$$

Gradient descent & Adam

Bien entendu, la fonction coût permet d'identifier les différences entre les valeurs réelles et les valeurs prédites, mais tout comme pour la régression linéaire et la régression logistique, nous avons besoin d'un algorithme pour trouver l'optimal local, c'est à dire de minimiser la fonction coût en identifiant les valeurs $w$ et $b$ qui permettront de réaliser les meilleures prédictions.

Jusqu'à présent, nous avions abordé les étapes de l'algorithme du gradient descent qui correspondent à appliquer la fonction coût, calculer les dérivés de $w$ et $b$ pour identifier la manière de mettre à jour les paramètres à chaque itération de l'algorithme ( diminuer la valeur ou augmenter la valeur ).

Nous avons vu également que dans le cadre de l'application de ces dérivées, nous devons renseigner, en tant que data scientist, une valeur alpha $α$ - fixe - mais qui, combinée avec les dérivées, permet de définir la « grandeur des pas » pour se diriger vers l'optimal local et qui diminuera au fur et à mesure de l'approche de cet optimal. Le problème de cette valeur alpha $α$, c'est que nous ne savons pas à l'avance définir pour notre modèle la meilleure valeur et par conséquent, nous testons plusieurs solutions : $(0,1 ; 0,03 ; 0,01 ; 0,003 ; 0,001 ;$ etc.). Sachant que lorsque alpha fait de trop grands pas, il risque de rater l'optimal local et nous voyons dans ce cas une redéfinition des valeurs $w$ et $b$ dans le sens inverse.

astuce

Gradient descent

$J(w, b) = \frac{1}{2m} \sum_{i=1}^n ((w \cdot x^{(i)} + b) - y^{(i)})^2$

1. $temp_w = w - \alpha \frac{d}{dw} J(w, b) = w - \alpha \frac{1}{m} \sum_{i=1}^{m} [f_{w,b}(x^{(i)}) - y^{(i)}] x^{(i)}$ ;
2. $temp_b = b - \alpha \frac{d}{db} J(w, b) = b - \alpha \frac{1}{m} \sum_{i=1}^{m} [f_{w,b}(x^{(i)}) - y^{(i)}]$ ;
3. $w = temp_w$ ;
4. $b = temp_b$ ;

Adam - pour Adaptive Moment Estimation - est un algorithme qui fonctionne comme le gradient descent, si ce n'est qu'il ne va pas utiliser une seule valeur de alpha $a$ mais utilisera des valeurs différentes pour chaque paramètre de notre modèle, c'est à dire des valeurs différentes pour chaque neurone. Il est donc considéré comme un optimiseur adaptatif du gradient descent qui ajuste le taux d'apprentissage pour chaque paramètre, offrant une convergence plus rapide et plus stable.

Si par exemple, notre modèle comprend 15 valeurs de $w$ :

$$temp_{w1} = w_1 - \alpha_1 \frac{d}{dw_1} J(w, b)$$$$...$$$$temp_{w15} = w_{15} - \alpha_{15} \frac{d}{dw_{15}} J(w, b)$$$$temp_b = b - \alpha_16 \frac{d}{db} J(w, b)$$

Dans ce cas, chaque alpha sera différent et Adam va les adapter au fur et à mesure en considérant que si pour les premiers paramètres, certaines petites valeurs de alpha appliquées aux dérivées permettent d'aller dans une certaine direction alors ces valeurs d'alpha peuvent continuer à augmenter de manière plus importante pour les paramètres suivants et par conséquent arriver plus rapidement à l'optimal local. L'inverse est également applicable, c'est à dire que adam va commencer à réduire de manière significative les pas.

Epochs

Un epoch - ou époque - représente dans le cadre des réseaux de neurones un cycle complet de passage des données d'entrainement à travers un réseau de neurones.

Un epoch contient donc trois phases :

• Phase 1 : propagation avant
• Phase 2 : application de la fonction coût et calcul de l'erreur
• Phase 3 : rétropropagation ( propagation arrière ) pour corriger les poids en fonction du gradient de l'erreur

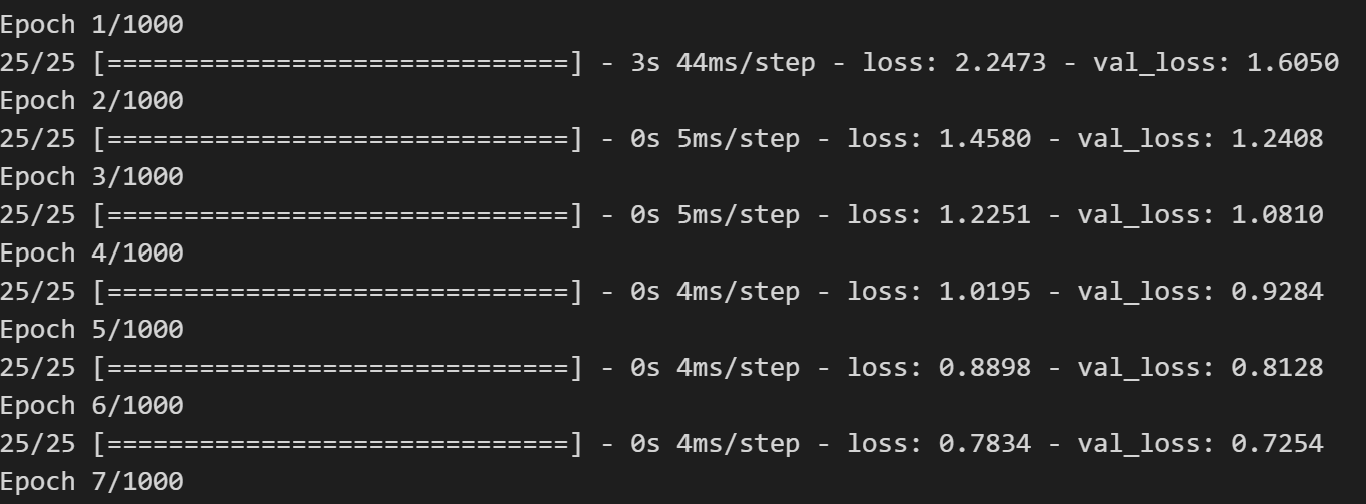
Nous devons en tant que data scientist, définir de manière arbitraire le nombre d'epochs. Il s'agit en réalité de ce que l'on nomme un hyperparamètre. Il détermine en effet combien de fois l'ensemble des données d'entrainement sera présenté au réseau dans le but de réaliser l'apprentissage.

En général, nous définissons un nombre d'epochs important et, nous intégrons dans l'algorithme ce que l'on appelle un « early stop », c'est à dire un arret anticipé du modèle sur base de la valeur de réduction coût qui est calculée à chaque itération, en spécifiant que si le coût ne diminue pas d'une certaine valeur ( exemple < 0.000001 ) alors le modèle est suffisamment entrainé.

Batch Size

Le batch size ou taille du lot est également un hyperparamètre que nous devons en tant que data scientist spécifier lors de l'entrainement d'un modèle de réseau de neurones. Il s'agit d'une particularité au réseau de neurones étant donné que ce dernier est fort utilisé dès lors que les données d'entrainement représentent un volume considérable et par conséquent, la plupart des éditeurs de code et bibliothèques associées aux réseaux de neurones sont conçues pour exploiter un maximum le calcul via les GPU ( Graphic Process Unit ).

Concrètement l'application d'un batch-size consiste à subdiviser les données d'apprentissage en échantillons de phases d'apprentissage qui sont traités par une itération du gradient descent (ou Adam). L'application du batch size sur de grands ensembles de données favorise efficacité de calcul mais surtout permet une convergence plus rapide et également d'éviter le sur-apprentissage.

Les valeurs préconisées sont en générale :32, 64, 128, 256, 512, 1024, 2048 car les Gpu sont optimisés pour les puissance de $2$. En général des petits valeurs sont choisies (32 ou 64) pour améliorer la généralisation mais il est important de savoir qu'un batch size plus important - qui nécessite plus de mémoire GPU - permet un entrainement plus rapide.

Fonctions d'activation

Dans un réseau de neurones, nous avons vu que chaque neurone dispose de ses propres paramètres $w$ et $b$. Nous verrons dans la section suivante que lors de la création d'un réseau de neurones en python, nous définissons par couche une fonction d'activation. Une fonction d'activation c'est un peu comme de déterminer par couche de neurones si le réseau doit appliquer à chaque neurone une régression logistique ou linéaire. Bien entendu, c'est un peu plus complexe que cela étant donné qu'il existe d'autres fonctions - plus évolutives - permettant de réaliser des calculs plus rapide et par conséquent de rendre le réseau de neurones plus efficient.

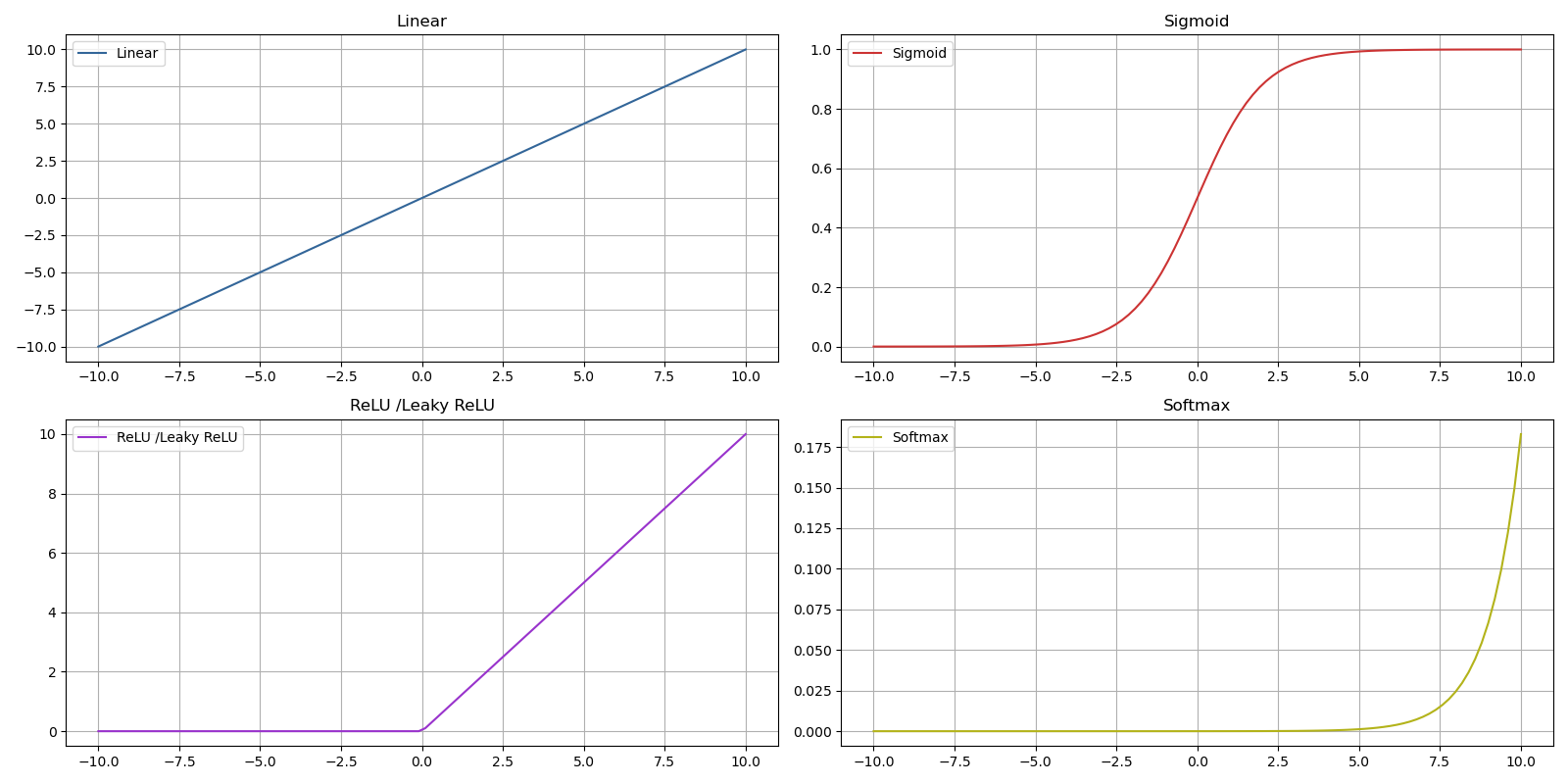
Les fonctions les plus courantes de nos jours sont :

• ReLu - Rectified Linear Unit - Cette fonction est la plus utilisée pour les couches cachées d'un réseau de neurones car son calcul est simple et par conséquent rapide ( convergence plus rapide en comparaison avec d'autres fonctions ) et elle permet surtout d'éviter la saturation des gradients pour les valeurs positives
• Leaky ReLu une variante du ReLu qui évite les neurones désactivés par la fonction ReLu en faisant en sorte que même si un neurone reçoit une entrée négative, il peut encore disposer d'une valeur de sortie très petite mais non nulle
• Sigmoïd fonction utilisée davantage en sortie de couche ou pour l'ensemble des couches lorsqu'il s'agit d'un problème de classement binaire car dans d'autres cas sa convergence est plus lente que ReLu
• SoftMax est une fonction d'activation utilisée en sortie de couche pour des classements multiclasses et permet une interprétation de plusieurs classes sur base de probabilités
• Linear cette fonction est principalement utilisée en couche de sortie pour un problème d'estimation

Les fonctions d'activation Tahn, SoftmaxPlus et Elu sont moins couramment utilisées de nos jours et donc nos reprises dans le présent document.

Code Pyhton complet

Le code ci-dessous est utilisé pour une estimation.

Pour un classement, les principes suivants doivent être modifiés :

• Fonction d'activation couche de sortie - sigmoid pour classement binaire, softmax pour multiclasses
• La fonction coût dans model.compile ('binary_crossentropy' pour un classement binaire et 'categorical_crossentropy' pour un classement multiclasses)
• La métrique d'évaluation dans model.compile : metrics=['accuracy']

Enfin en cas de classement multiclasse, $y$ doit être représenté en encodage one-hot de sorte à obtenir autant de $y$ que de classe. La prédiction définira alors une probability pour tous les $y$.

import pandas as pd
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error


data = pd.read_csv('data.csv')
x = data[['x_1', 'x_2', 'x_3', 'x_4', 'x_n']].values  
y = data['y'].values  

scaler_x = StandardScaler()
scaler_y = StandardScaler()

x = scaler_x.fit_transform(x)
y = scaler_y.fit_transform(y.reshape(-1, 1))

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4, random_state=42)

def build_models():
    tf.random.set_seed(20)
    
    model_1 = Sequential([
        Dense(8, activation='relu', input_shape=(x_train.shape[1],)),
        Dense(4, activation='relu'),
        Dense(1, activation='linear')
    ], name='model_1')

    model_2 = Sequential([
        Dense(16, activation='relu', input_shape=(x_train.shape[1],), kernel_regularizer=tf.keras.regularizers.l2(0.01)),
        Dense(8, activation='relu', kernel_regularizer=tf.keras.regularizers.l2(0.01)),
        Dense(1, activation='linear')
    ], name='model_2')

    model_3 = Sequential([
        Dense(32, activation='relu', input_shape=(x_train.shape[1],), kernel_regularizer=tf.keras.regularizers.l2(0.01)),
        Dense(16, activation='relu', kernel_regularizer=tf.keras.regularizers.l2(0.01)),
        Dense(1, activation='linear')
    ], name='model_3')

    model_4 = Sequential([
        Dense(64, activation='relu', input_shape=(x_train.shape[1],), kernel_regularizer=tf.keras.regularizers.l2(0.01)),
        Dense(32, activation='relu', kernel_regularizer=tf.keras.regularizers.l2(0.01)),
        Dense(16, activation='relu', kernel_regularizer=tf.keras.regularizers.l2(0.01)),
        Dense(1, activation='linear')
    ], name='model_4')
    
    model_list = [model_1, model_2, model_3, model_4]
    
    return model_list


nn_models = build_models()


for model in nn_models:
    model.compile(
        loss='mse',
        optimizer=tf.keras.optimizers.Adam(learning_rate=0.01)
    )
    
    print(f"Training {model.name}...")
    
    model.fit(
        x_train, y_train,
        epochs=1000,
        batch_size=32,
        validation_split=0.1,
        verbose=0
    )
    
    print("Done!\n")


    yhat_train = model.predict(x_train)
    yhat_test = model.predict(x_test)
    
    rmse_train = mean_squared_error(y_train, yhat_train, squared=False)
    rmse_test = mean_squared_error(y_test, yhat_test, squared=False)
    
    print(f"Model {model.name} - RMSE on Training Set: {rmse_train:.4f}")
    print(f"Model {model.name} - RMSE on Test Set: {rmse_test:.4f}\n")

Prévision pour un nouvel enregistrement :

X_new = [[0, 0, 0, 0, 0]]  

X_new_scaled = scaler_x.transform(X_new)

y_new_scaled = model.predict(X_new_scaled)

y_new = scaler_y.inverse_transform(y_new_scaled)
print(y_new)