Composantes principales

Comme nous l'avons vu dans le chapitre sur la sélection des variables, la précision et la rapidité de calcul d'un modèle sont fortement impactés par le choix des variables utilisées pour un modèle supervisé ou non supervisé.

Pour rappel, la plupart des techniques statistiques sont exécutées par le CPU (Central Processing Using) et utilisent la mémoire vive de l'ordinateur (RAM) pour stocker l'information. Certaines techniques, plus gourmandes, font également appel au GPU (Graphic Process Unit), un coprocesseur graphique qui va pouvoir alléger la tâche du CPU. L'idée de l'analyse en composantes principales est de pouvoir réduire la dimensionalité des données afin d'assurer une certaine efficience.

Rappel dimensionalité

La dimensionalité correspond en fait au nombre de colonnes x nombre de lignes. Il est important de comprendre qu'au plus nous utilisons de variables dans un algorithme pour l'application d'une technique statistique, au plus le nombre d’enregistrements pour assurer un apprentissage sera important. La dimensionalité sera donc moins importante et par conséquent cela aura un impact sur les performances de calcul ainsi que sur le risque de sur-apprentissage.

La sélection / réduction des variables est une première manière de pouvoir réduire la dimensionalité. Il existe toutefois des techniques spécifiques permettant de réduire la dimensionalité dont l'analyse en composantes principales est la plus générale, c'est à dire applicable dans la création d'algorithmes supervisés ou non supervisés.

**L’analyse en composantes principales est donc une méthode de réduction des dimensions qui permet de réduire le nombre de variables étudiées (champs / variables d’une table) en perdant le moins d’information possible ( enregistrement ).

Relations linéaires

L'analyse en composantes principales peut s'appliquer dans tous les cas, et sera particulièrement efficace dans le cadre d'une colinéarité, c'est à dire une corrélation entres les prédicteurs dans une technique supervisée.

L’analyse en composantes principales vise à mettre en évidence des relations linéaires fortes entre les variables, à transformer ces dernières en de nouvelles variables « décorrélées » contenant la majorité de l’information (composantes principales) et dont l’espace dimensionnel est moindre ( variables et enregistrements ). Cette méthode est particulièrement utile lorsque le nombre de variables est important.

On obtient donc un nombre de variables limités qui correspondent à des combinaisons linéaires pondérées des variables originales et qui conservent la majorité de l’information de l’ensemble des données originales.

Transformation statistique & géométrique

C’est une technique à la fois :

• Statistique : identification des composantes principales soit les directions qui captent la majorité de la variation des données
• Géométrique : l’espace subit une rotation ; Les points sont projetés dans une nouvelle direction de dimensions moindres mais contenant la majorité de l’information de l’espace original

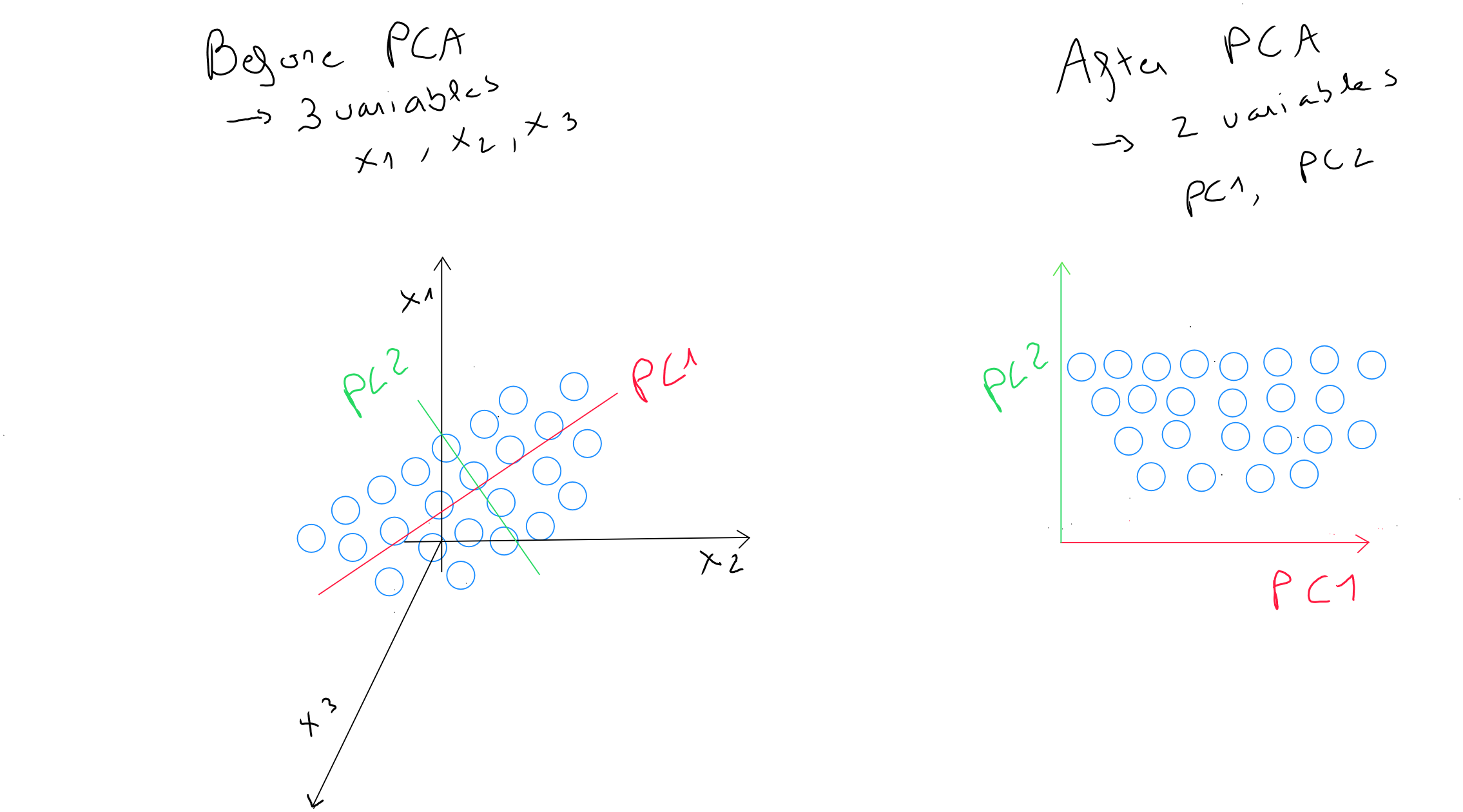
L'étape statistique consiste à identifier une combinaison linéaire de deux variables qui contient le plus – si ce n’est pas l’entièreté – de l’information. Cette combinaison linéaire est nommée $PC1$, composante principale et remplace les deux variables initiales. La composante principale représente donc la direction dans laquelle la variabilité des points est la plus large. Il s’agit de la droite qui saisit le plus de variation dans les données si nous décidons de réduire la dimensionalité des données de $2$ à $1$. Il s’agit également de la droite qui minimise la somme des carrés des distances perpendiculaires des points par rapport à elle-même.

Nous identifions ensuite la droite perpendiculaire à la composante principale qui contient la seconde variabilité plus importante entre les points. Le fait de sélectionner la perpendiculaire à la composante principale $1$, nous assure d'obtenir une composante principale $2$ décorrélée.

L'étape géométrique consiste en une rotation orthogonale des axes dans le but de pouvoir choisir moins de composantes que de variables initiales. La rotation ne change que les coordonnées des points et permet de redistribuer la variabilité afin de capturer un maximum de l’information.

Par exemple, si nos variables « poids », « taille » et « âge » contiennent les valeurs $75$, $187* et *35$, et qu'elles sont redistribuées dans un nouvel espace géométrique de deux composantes principales PC1 et PC1, nous avons deux valeurs $148.5$ pour PC1 et $-51.8$ pour PC2. Ces deux valeurs sont différentes des trois valeurs initiales mais respectent la même notion de distance et nous avons réduit notre dimensionalité d'un axe.

Sélection des composantes et variance

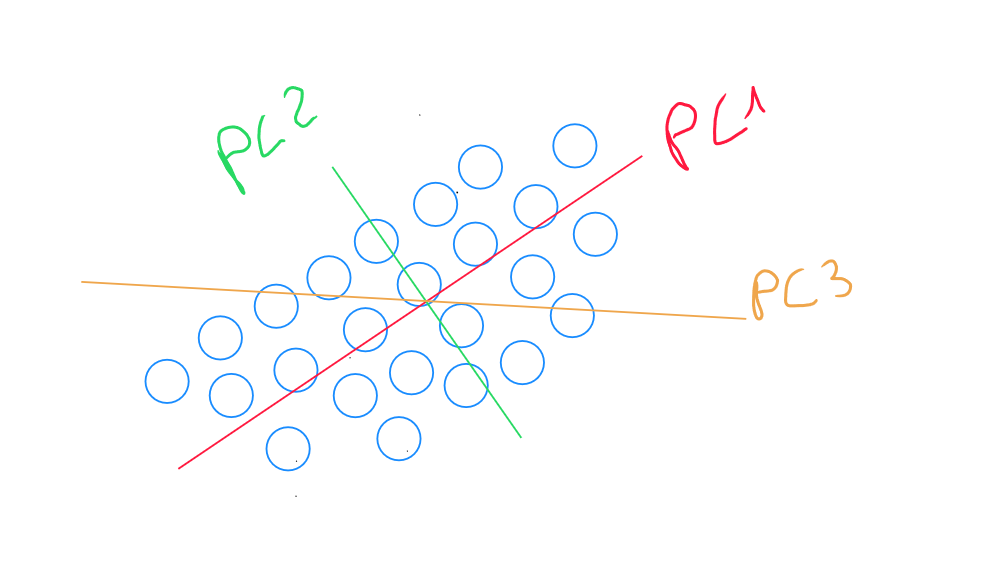
Si nous disposons de nombreuses variables, l'identification de la composante principale 3 explique la variance restante dans une dimension perpendiculaire aux deux premières composantes principales. En conséquence, la variance capturée par PC3 est moindre que celle capturée par PC1 et PC2, mais elle est toujours présente. PC3 capture les variations qui ne sont pas alignées avec les directions de PC1 et PC2. l'identification de composantes supplémentaires est similaire aux étapes précédentes.

La quantité de variance expliquée par chaque composante principale qui est mesurée va nous permettre de déterminer le nombre de composantes optimales soit la proportion cumulée de variance des données après ajout de chacune des composantes principales.

Par exemple, pour un modèle de 20 variables, il est possible que dès la 2e composante principale, 99% de la variance de l'information soit capturée et par conséquence, nous réduisons l'espace dimensionnel de 20 variables à 2 composantes

Code python

En pré-traitement, toutes les données doivent être numérisées soit dans le cadre d'un encodage one-hot soit par le processus de numérisation de variables discrètes.

data = pd.read_csv('data.csv')

pcs = PCA()
pcs.fit(data.dropna(axis=0))
pcsSummary= pd.DataFrame({'Standard deviation': np.sqrt(pcs.explained_variance_),
                         'proportion of variance': pcs.explained_variance_ratio_,
                         'cumulative proportion': np.cumsum(pcs.explained_variance_ratio_)})
pcsSummary = pcsSummary.transpose()
pcsSummary.columns= ['PC{}'.format(i) for i in range(1,len(pcsSummary.columns)+1)]
pcsSummary.round(4)

pcsComponents_df = pd.DataFrame(pcs.components_.transpose(),columns=pcsSummary.columns,index=data.columns)
pcsComponents_df