Sélection des variables

La sélection des variables consiste à sélectionner un sous-ensemble de variables pertinentes au regard de l'ensemble des variables disponibles dans la source de données. Cette étape est tributaire :

• De l'objectif du projet data ;
• De l'analyse statistique univariée de l'ensemble des variables ;
• Du choix de la technique statistique qui sera appliquée et des variables requises pour la création de l'algorithme ;
• De techniques spécifiques en statistique ;
• Du choix arbitraire du data scientist ;
• ...

La malédiction de la dimensionalité

En tant que data scientist, nous devons comprendre un élément crucial concernant les qualités attendues d'un modèle et plus particulièrement la précision et la rapidité du calcul du modèle. Ces deux éléments seront fortement impactés par le choix des variables.

La plupart des techniques statistiques sont exécutées par le CPU ( Central Processing Using ) et utilisent la mémoire vie de l'ordinateur (RAM) pour stocker l'information. Certaines techniques, plus gourmandes, font également appel au GPU ( Graphic Process Unit ), un coprocesseur graphique qui va pouvoir alléger la tâche du CPU. Certaines librairies Python sont d'ailleurs optimisées pour l'utilisation du GPU. L'idée dans la sélection des variables est de prémâcher le travail pour assurer une certaine efficience.

La dimensionalité correspond en fait au nombre de colonne x nombre de lignes. Il est important de comprendre qu'au plus nous utilisons de variables dans un algorithme pour l'application d'une technique statistique, au plus le nombre d’enregistrements pour assurer un apprentissage sera important. La dimensionalité sera donc importante et par conséquent cela aura un impact sur les performances de calcul.

Prenons l'exemple suivant - un jeu d'échec :

Imaginons que l'axe des ordonnées est Y ( chiffres de $1$ à $8$ ) et l'axe des abscisses est x ( lettres de a à h ). Si nous sommes limités par un jeu d'échec pour disperser nos données, nous avons la possibilité de placer $64$ enregistrements. Nous sommes en deux dimensions - nous avons sélectionné deux variables - $(x,y)$ et par conséquent nous avons en tout $64$ cases disponibles. Si nous décidons d'ajouter une troisième variable, la variable Z :

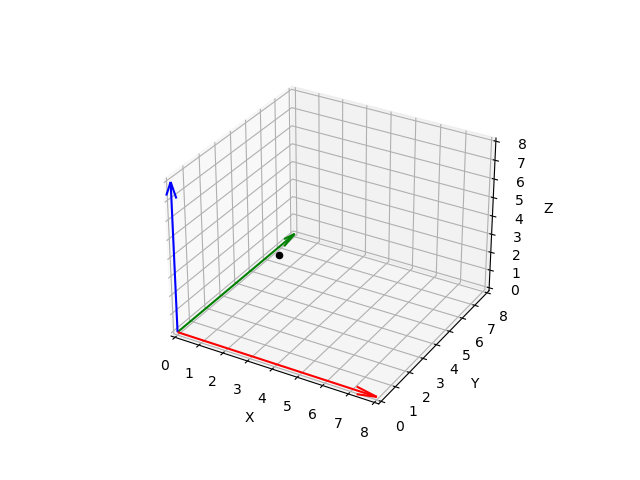
Nous augmentons l'espace de 64 cases à 512. Or, il est important de comprendre que si nous voulons éviter un sous-apprentissage, nous devons disposer de suffisamment de dispersion des enregistrements dans cet espace. la règle est : au plus nous avons de variables, au plus nous avons besoin d'enregistrements.

Mais cela doit être sujet à réflexion car :

• Plus nous intégrons des variables, plus le modèle sera complexe, plus le nombre d’enregistrements dont nous aurons besoin pour évaluer les relations entre les variables sera élevé


• Plus le nombre d’enregistrements sera élevé, plus il y aura de valeurs manquantes à traiter


• Plus le nombre de variables sera important, plus il y aura un risque d’existence de sous-ensembles de variables fortement corrélées. Inclure des variables fortement corrélées peut mener à des problèmes de précision ou de fiabilité

L'objectif est donc de réduire le nombre de variables tout en s'assurant d'éviter un sous-apprentissage. Plusieurs options s'offrent au data scientist telles qu' (1) ignorer les variables non pertinentes par rapport à l'objectif à atteindre ; (2) ignorer certains variables trop corrélées entre elles et dont la prise en compte simultanée enfreindrait l’hypothèse recherchée de non-colinéarité ( indépendance linéaire ) des variables explicatives ( prédicteurs ) ; (3) utiliser des techniques statistiques telles que l'analyse en composantes principales, la sélection ascendante / descendante - régression ou encore l'application d'un arbre de décision pour identifier les variables les plus corrélées avec la variable cible.

Corrélation

Pour comprendre la corrélation, il est important de rappeler la notion de variance et de définir la covariance. Comme nous l'avons vu dans la partie statistique univariée, la variance est une mesure de la dispersion des valeurs d'une variable autour de sa moyenne. Elle correspond à la moyenne des carrés des écarts à la moyenne et est toujours positive. Elle indique si une distribution est homogène ou hétérogène. Concrètement, si une variance est nulle, cela signifie que toutes les valeurs des enregistrements sont égales à la moyenne - la distribution est parfaitement homogène -. Le variance n'est pas interprétable en tant que telle car elle mesure l'écart au carré de la moyenne (qui est nécessaire pour éviter que les valeurs positives et négatives s'annulent), mais le meilleur indicateur est bien entendu l'écart par rapport à la moyenne, à savoir l'écart-type.

La variance est utile pour comparer deux variables ensemble afin de caractériser les variations simultanées de deux variables. On parle alors dela covariance qui mesure la force de la relation entre deux variables. Concrètement, si deux variables présentent une covariance importante - par exemple $70$, cette information met en avant une relation linéaire entre les deux variables. Si nous analysons la covariance entre un prédicteur $x$ et la variable prédite $y$, dans ce cas nous pourrions affirmer que $x$ est un bon prédicteur pour $y$.

Formule de la covariance : $s_{x,y} = \frac{\sum_{i=1}^{n} (x_i - \bar{x}) (y_i - \bar{y})}{n - 1}$

Toutefois, ce n'est pas entièrement correct car la covariance n'est pas normalisées et est, de part ce fait, sensible aux unités de mesure. Il est donc important de considérer la forme normalisée de la covariance, à savoir la corrélation.

La corrélation mesure la force et la direction - qu'elle soit positive ou négative - entre deux variables. Si l'une des variables $x$ ( prédicteur ), présente une corrélation élevée avec la variable cible ( y ), cela nous indique que ce prédicteur particulier influence fortement la variable cible - il est donc discriminant et très important pour le modèle - et la corrélation nous indique également si cet impact est positif ou négatif sur les valeurs de la variables $y$.

La corrélation étant la covariance normalisée, sa valeur sera toujours comprise entre -1 ( corrélation parfaite et négative ) et + 1 ( corrélation parfaite et positive ). Une corrélation de 1 définit que l'augmentation de la variable A aura le même impact sur la variable B ( positive ou négative ). A contrario, une corrélation de 0 indique l'absence d'une relation linéaire entre les deux variables ( l'augmentation de la variable A n'a aucun impact sur la variable B ).

Formule de la corrélation : $r_{x,y} = \frac{\sum_{m=1}^{n} (x_{m} - \bar{x})(y_{m} - \bar{y})}{\sqrt{\sum_{m=1}^{n} (x_{m} - \bar{x})^2} \sqrt{\sum_{m=1}^{n} (y_{m} - \bar{y})^2}}$

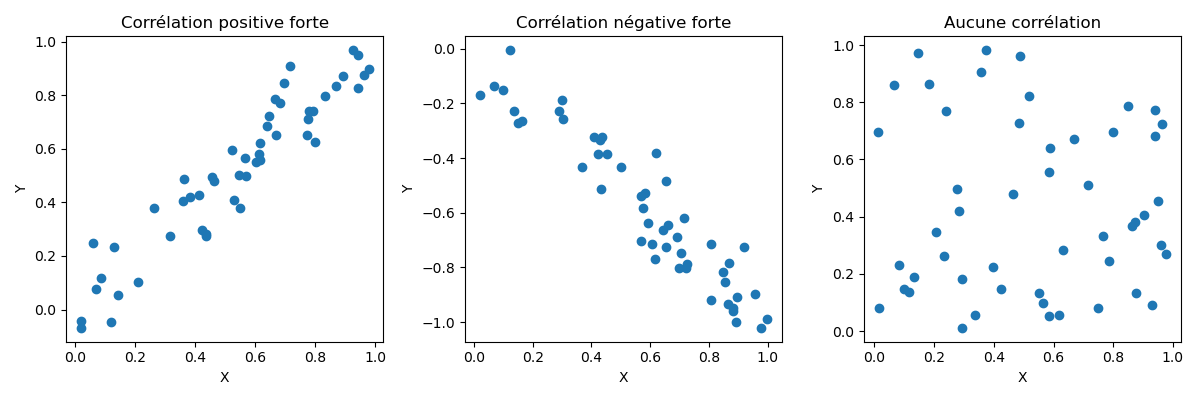
Nous souhaitons donc identifier les variables $x$ les plus corrélées avec la variable cible $y$. Par exemple, la superficie d'une maison est grande, au plus le prix est élevé ( force importante car variable qui influence le plus et direction positive car elle augmente le prix ). A contrario, au plus le kilométrage d'une voiture est élevé, au plus le prix de la voiture diminue. Dans ce cas, la variable "kilométrage" a une incidence importante sur le prix ( force ) et la direction est négative.

astuce

Pour résumer : La covariance est une extension de la notion de variance. La corrélation est la forme normalisée de la covariance. Au plus une variable $x$ est corrélée ( de manière positive ou négative ) à la variable $y$, au plus elle est importante pour notre modèle car on dit qu'elle est "discriminante".

Colinéarité

La colinéarité est une situation dans laquelle deux variables sont associées de manière linéaire ( corrélation élevée ) et sont utilisées comme des prédicteurs de la variable cible. Cela signifie que deux variables $x ( x_1 et x_2 )$ sont corrélées de manière positive ou négative et sont utilisées en tant que prédicteurs. Cette situation doit être évitées car elle rend difficile l'identification de l'effet indépendant de chacune des variables $x$ sur la variable prédite $y$.

Pour la majorité des techniques - à l'exception des réseaux de neurones -, il est essentiel d'éviter l'utilisation de variables $x$ corrélées. Les réseaux de neurones peuvent gérer cette situation par l'ajustement de poids mais la décorrélation des variables corrélées permet toutefois de d'aider l'algorithme à converger vers la situation optimale.

Multi-colinéarité

Attention qu'il est possible que deux variables $x_1$ et $x_2$ ne soient pas corrélées ensembles et de manière individuelle, $x_1$ n'est pas corrélée avec $x_3$ et $x_2$ n'est pas corrélée avec $x_3$ mais qu'ensemble, $x_1$ et $x_2$ sont corrélées à $x_3$, on parle alors de multi-colinéatiré

Techniques

Comme nous l'avions mentionné en début de ce chapitre, notre objectif en tant que data scientist est d'optimiser nos modèles, c'est-à-dire de les rendre le plus efficient possible. L'efficience sous-entend la notion de précision mais également de rapidité et de robustesse.

Ingénierie des caractéristiques

La première option du data scientist est d'appliquer l'ingénierie des caractéristiques (Features engineering), il s'agit de sélectionner et transformer les variables les plus pertinentes, dans le but d'optimiser un modèle, c'est à dire d’obtenir de meilleurs performances. L'ingénierie des caractéristiques intègre dans la notion de création de nouvelles variables sur base de variables existantes mais également le regroupement de variables en une nouvelle variable calculée ou la transformation de variables existantes.

Prenons l'exemple de notre agence immobilière. Les données à notre disposition pour prédire le prix de vente des maisons comprend notamment deux variables : $x_8$ = largeur du terrain & $x_9$ = la longueur du terrain. Si nous analysons $x_8$ et $x_9$ dans les étapes de préparation, nous devrions identifier une certaine corrélation positive et, ces variables étant utilisées en tant que prédicteurs, nous pourrions affirmer que nous avons un problème de colinéarité. Dans cet exemple, une manière de supprimer cette colinéarité est de créer une nouvelle variable $x_[10]$ qui serait l'aire du terrain et dont les valeurs correspondrait à la multiplication entre la variable $x_8$ et $x_9$. $x_{10}$ serait donc la variable finale utilisée en tant que prédicteur.

Application d'algorithmes

Il existe certains algorithmes spécifiques d'aide à la sélection de variable. Par exemple, les méthodes de sélection ascendante ( forward selection ) et descendante ( backward selection ) des techniques de régression qui permettent d'identifier l'impact de l'ajout ou de la suppression de variables sur l'évaluation globale d'un modèle.

L'arbre de décision est une technique statistique très intéressante lorsqu'il s'agit d'aider à la sélection de variables discriminantes. Bien qu'il s'agisse également d'une technique statistique supervisée - et donc de prédiction -, elle peut être utilisée dans l'algorithme de préparation d'un autre modèle de prédiction. La technique de l'arbre privilégie la séparation des enregistrements en sélectionnant dans le premier noeud, la variable qui sépare au mieux ces enregistrements, c'est à dire qui améliore le score de pureté.

L'analyse en composantes principales (ACP) est une technique non-supervisée fortement appliquée dans le cadre la sélection de variables utilisées en tant que prédicteurs et corrélées entre elles. Cette technique va redistribuer les valeurs des variables corrélées dans un nouvel espace géométrique de dimensions moindres (les composantes principales) en identifiant la droite qui traverse la majorité des informations entre plusieurs variables ainsi que les droites suivantes et perpendiculaires, ce qui permet d'obtenir des composantes principales décorrélées.