Ingénierie des variables

La transformation des données, également appelée l'ingénierie des caractéristiques (Features Engineering), comprend l'ensemble des étapes impliquant la préparation des variables sélectionnées. Il peut s'agir de remplacer les valeurs manquantes ou aberrantes, transformer des variables existantes ou créer de nouvelles variables sur base de variables existantes.

Remplacement des valeurs manquantes ou aberrantes

La première opération de cette phase de transformation consiste à fiabiliser, remplacer ou supprimer les valeurs incorrectes,manquantes ou aberrantes. Dans certaines situations, nous sommes confrontés en tant que data scientist à des données erronées.

Par exemple, dans le tableau ci-dessous, reprenant des informations globale de clients d'un supermarché :

ID	Code Postal	Genre	Age	Ventes	Encodage
2345	7000	C	44	32	25/04/2011 10:09
...	...	...	...	...	...
MRF998764	1050	M	46	98,1	03/09/2024 15:34
MRF998765	5000		0	42,53	03/09/2024 14:38
MRF998766	1180	F	42	2354,95	03/09/2024 15:43
MRF998767	4000	F	50	32,3	03/09/2024 15:50
MRF998768	75000	M	35	112,54	03/09/2024 15:57
MRF998769	6600	F	30	-999999	03/09/2024 15:58

Nous pouvons identifier plusieurs cas d'enregistrements erronés tels que le genre qui correspond à « C » ; l'âge à « 0 » ; le montant d'achat à « -999999 » ou encore le code postal d'un pays étranger. Bien entendu le plus simple dans ce cas de figure est de décider de supprimer ces enregistrements et de ne pas les considérer. Toutefois, pour des besoins spécifiques liés à la techniques ou pour d'autres variables, si nous souhaitons garder ces enregistrements, il est possible d'appliquer diverses techniques afin de remplacer ces valeurs considérées comme aberrantes ou les valeurs manquantes.

La démarche la plus simple serait de remplacer ces valeurs par une constante. Cette constante peut être peut être générée de diverses manières :

Remplacer ces valeurs par la moyenne ( variable continue ) : cette méthode est très simples mais il est important de considérer que dans ce cas, la mesure de la répartition va se réduire artificiellement.

Remplacer ces valeurs par la médiane ( variable continue ) : de nouveau, cette méthode est relativement simple mais la médiane ne représente pas forcément la valeur la plus fréquente.

Remplacer ces valeurs par le mode ( variable continue ou discrète ) : le mode étant la valeur présentant la fréquence la plus importante, cette méthode est plus robuste que les deux précédentes d'autant qu'elle s'applique à tous type de variables

Il est également possible de remplacer par une valeur qui serait plus représentatative de la réalité. Comme par exemple :

Remplacer ces valeurs par une variable générée aléatoirement à partir de la distribution des données : nous partons du principe que l'aléatoire est dans un certain sens plus juste car il n'amènera pas une valeur prédominante

Utiliser une technique statistique supervisée : cette méthode est la plus fiable mais plus consommatrice en terme de procédé. Nous utilisons les valeurs des autres variables pour prédire les valeurs manquantes

Utiliser une technique statistique non-supervisée comme par exemple le clustering qui permet d'identifier un groupe d'enregistrements auquel l'enregistrement appartient et prendre la moyenne de la valeur pour la variable contenant une valeur manquante ou erronée

De manière générale, La proportion d’enregistrements considéré comme incorrects ou aberrants ne devrait pas dépasser 1 à 2 %.

Création de nouvelles variables

Dans la plupart des cas, nous devrons en tant que data scientist, identifier les variables pertinentes ( Sélection des Variables ) et, par conséquent, « supprimer » de nos données finales de nombreuses variables. Toutefois, nous serons également amené pour des besoins spécifiques à créer de nouvelles variables sur base de variables existantes. Il s'agit en réalité de nouvelles variables créées à partir de fonctions ou des calculs appliquées à des variables existantes.

Exemple 1 : dans un set de données de ventes, nous disposons de la variable quantité et la variable prix pour chaque article vendu, nous pourrions à partir de ces variables créer la variable « Montant » qui correspondrait à [Quantity] * [UnitPrice].

df = pd.DataFrame(data)
df['Montant'] = df['Quantity'] * df['UnitPrice']

Exemple 2 : nous disposons dans un set de données la date de naissance d'un client, nous avons besoin de l'âge de chaque client, pour cela nous pouvons appliquer la fonction « age »/

def calculer_age(date_naissance):
aujourd_hui = date.today()
age = aujourd_hui.year - date_naissance.year
if (aujourd_hui.month, aujourd_hui.day) < (date_naissance.month, date_naissance.day):
  age -= 1

return age

Exemple 3 : calculer la durée de vie d’un client (Date dernier achat - Date premier achat)

import pandas as pd
df = pd.DataFrame(data)

df['PurchaseDate'] = pd.to_datetime(df['PurchaseDate'])

cust_lifetime = df.groupby('CustID')['PurchaseDate'].agg(['min', 'max'])
cust_lifetime['Lifetime'] = cust_lifetime['max'] - cust_lifetime['min']
cust_lifetime['Lifetime'] = cust_lifetime['Lifetime'].dt.days
cust_lifetime.drop(['min', 'max'], axis=1, inplace=True)

customer_lifetime

Exemple 4 : Fusionner des variables redondantes. Notre source de données contient deux colonnes « CustomerName » dans deux tables , nous souhaitons une colonne unique « CustomerName » ne chargeant que des valeurs distinctes.

import pandas as pd
data1 = {'customerName': ['Alice', 'Bob', 'Charlie', 'Alice']}
data2 = {'customerName': ['David', 'Eve', 'Alice', 'Frank']}
df1 = pd.DataFrame(data1)
df2 = pd.DataFrame(data2)

combined_df = pd.concat([df1, df2])

unique_customers = combined_df['customerName'].unique()

unique_customers

Transformation des variables

La troisième opération est la transformation de variables. En effet, certaines techniques statistiques n'acceptent que des variables quantitative comme prédicteurs et d'autres que des variables qualitatives. Il existe également des techniques qui acceptent les deux ( variables quantitatives & qualitatives comme prédicteurs ). Si la technique que nous utilisons n'accepte que des variables qualitative et que notre source de données contient des variables quantitative, nous pouvons transformer ces variables quantitative en variables qualitatives. Ce procédé s'appelle la discrétisation de variables continues. A l'inverse, si la technique que nous utilisons n'accepte que des variables quantitative et que notre source de données contient des variables qualitative, nous pouvons également trasnformer ces variables « en numérisant » les variables qualitatives ou en appliquant un hot-encoding.

Discrétisation des variables quantitatives

La discrétisation des variables quantitatives ( continues ) consiste à classer les valeurs d’une variable continue dans une classe spécifique.

Le défi majeur de la discrétisation est de définir les classes ( tranches ) de manière appropriée. Il n'existe pas de méthode universelle, et le choix dépendra de plusieurs facteurs, mais nous pouvons citer les principales :

L'analyse statistique univariée permettant de mettre en évidence la distribution de la variable, dont la forme de distribution peut suggérer des seuils « naturels »

L'objectif de l'analyse - les classes doivent être pertinentes pour la question de recherche ou le problème à résoudre

La discrétisation par quantile - définit les classes de sorte que chaque classe contienne un même nombre d'enregistrements

l'application d'une technique supervisée - l'arbre de décision pour identifier les seuils optimaux des classes

Numérisation des variables discrètes

Pour certaines techniques – notamment celles pour lesquels on devra calculer la distance entre deux enregistrements, une des préparations consistera à numériser des variables discrètes afin de pouvoir définir cette notion de distance.

Il suffit pour cela d'attribuer une valeur numérique aux valeurs existantes, nous appelons cela le procédé de « mapping ». Attention toutefois de considérer dans le cas d'une variable qualitative ordinale à respecter le caractère hiérarchique. Dans les autres cas ( pour les variables qualitatives nominale ), il suffit d'attribuer une valeur à chaque variable.

Appréciation	Note
Très bon	5
Bon	4
Moyen	3
Mauvais	2
Très mauvais	1

Genre	Note
Homme	1
Femme	0

L'encodage one-hot

Il est également possible d'utiliser le concept de l'encodage One-Hot qui consiste à encoder une variable à $n$ valeurs sur $n$ variables binaires. Les nouvelles variables contiennent des valeurs numériques à savoir 1 ou 0 et pourront être utilisée dans une technique requérant uniquement des variables quantitatives en tant que prédicteurs. Attention il s'agit d'une exception étant donné qu'une variable binaire ne représente pas une quantité ni une mesure.

Le one-hot encoding crée des colonnes binaires indépendantes pour chaque catégorie, évitant ainsi toute notion d'ordre ou de hiérarchie entre elles.

Note	Bon	Mauvais	Moyen	Très bon	Très mauvais
Très bon	0	0	0	1	0
Bon	1	0	0	0	0
Moyen	0	0	1	0	0
Mauvais	0	1	0	0	0
Très mauvais	0	0	0	0	1

df_encoded = pd.get_dummies(df, columns=['Appréciation'])
df_encoded

Normalisation & Standardisation

Le but de la normalisation et de la standardisation est de transformer les valeurs de variables quantitatives afin de les mettre sur une même échelle. La normalisation et standardisation sont deux techniques systématiquement appliquées dans la création de l'algorithme afin :

D’augmenter l’efficacité et la rapidité des processus, notamment lorsque l'algorithme utilise un processus d'optimisation itératif ( la descente de Gradient ou dérivé - ADAM ) ou lorsque la technique nécessite un calcul de la distance entre enregistrements.

Assurer une comparaison équitable / une réduction de la sensibilité à l’échelle afin d'éviter comme biais le fait qu'une variable n'influence pas intrinsèquement plus le résultat qu'une autre en raison de la différence d'échelle des mesures

Il s'agit donc de mettre sur une même échelle les valeurs des variables d'un ensemble de données pour qu'elles se situent dans une plage spécifique ou suivent une distribution particulière. Ces techniques sont réalisées principalement pour :

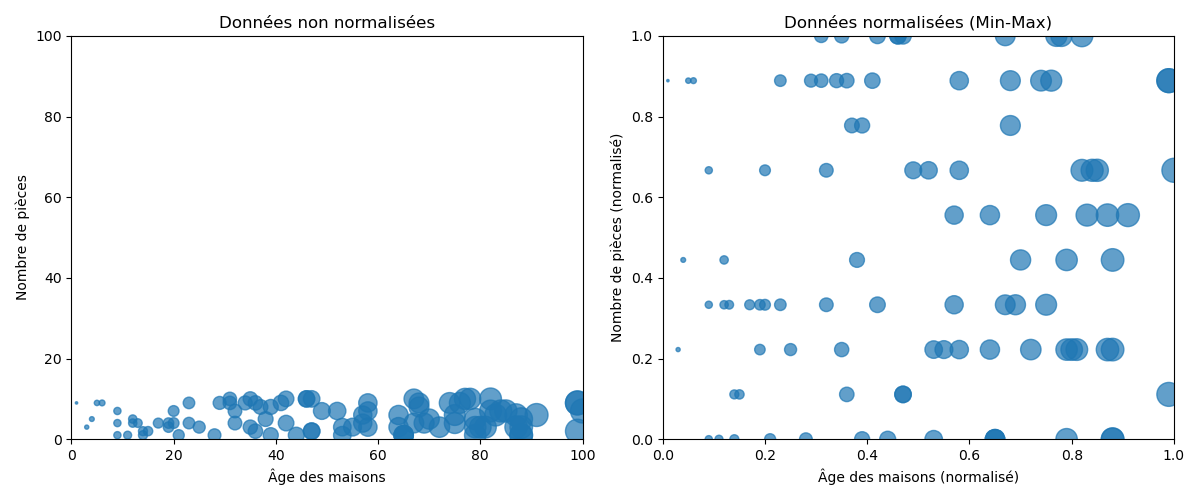
Le procédé de normalisation n’a besoin que du min et du max et l’idée est de convertir toutes les valeurs sur une échelle entre 0 et 1 tout en conservant les distances entre les valeurs.

X_{norm} = \frac{X - X_{min}}{X_{max} - X_{min}} \in [0, 1]

La normalisation est conseillée lorsque l’on ne connait pas la distribution des données ou lorsque l’on sait que la distribution n’est pas gaussienne ( en forme de cloche ). Elle est privilégiée pour des algorithmes qui ne font pas d’hypothèse sur la distribution des données comme les K-nearest neighbors ou les réseaux de neurones.

Normalisation MinMax

# Librairie Numpy
import numpy as np

def min_max_normalization(data):

 min_val = np.min(data)
 max_val = np.max(data)
 normalized_data = (data - min_val) / (max_val - min_val)
 return normalized_data

# Librairie Sickit-Learn
from sklearn.preprocessing import MinMaxScaler
import numpy as np

scaler = MinMaxScaler()
scaler.fit(data) # Calcul des Min & Max
normalized_data = scaler.transform(data)

normalized_data

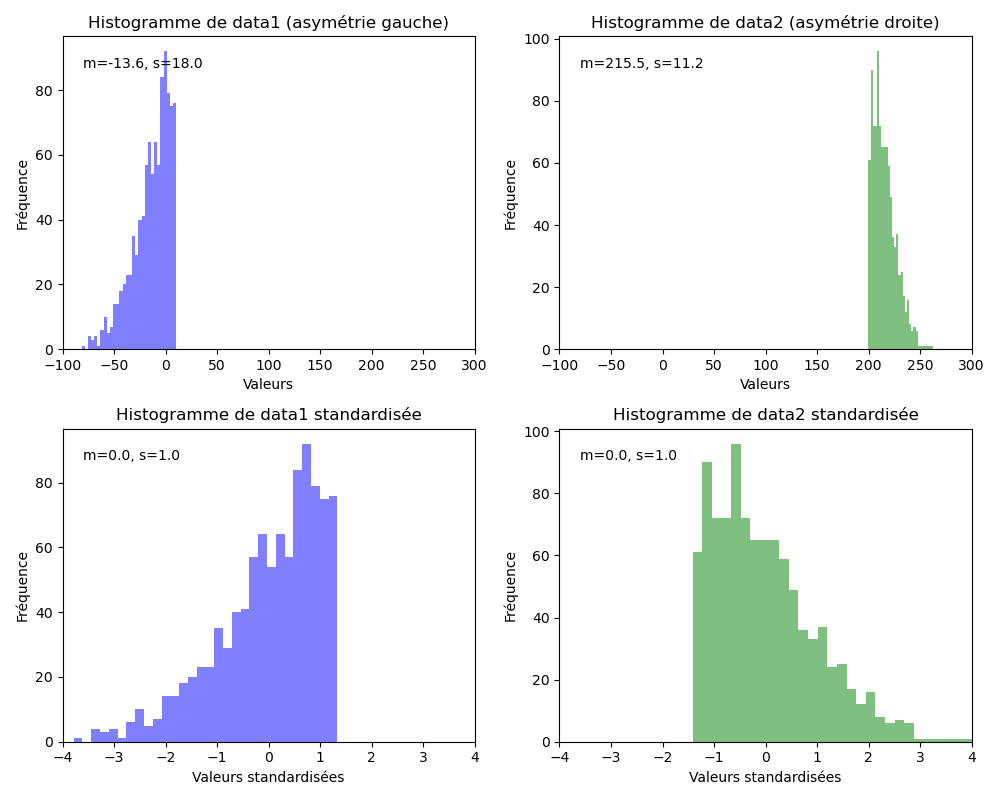
Le procédé de standardisation est plus subtil car il a également pour but de ramener la moyenne à 0 et l’écart-type à 1.

Z = \frac{X_i - \mu}{\sigma}

ou :

Z = \frac{x_i - \bar{x}}{\sqrt{\frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n}}}

La standardisation suppose que nos données ont une distribution gaussienne ( courbe en cloche ). Cela ne doit pas être strictement vrai, mais la technique est plus efficace si c'est bien le cas.

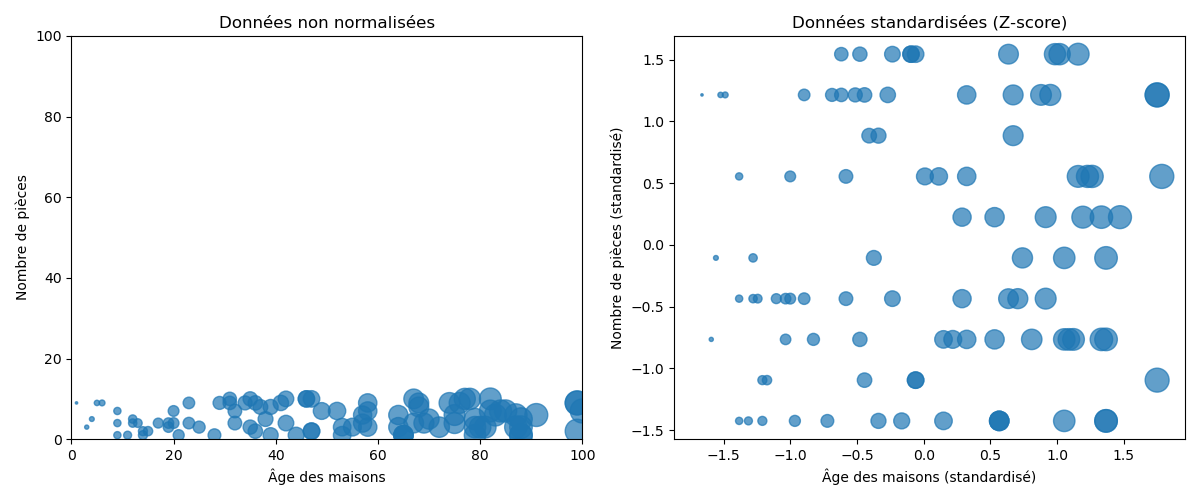
Standardisation

Les deux distributions ci-dessous sont ramenées à une moyenne à 0 afin d'aligner les échelles et éviter ainsi tout biais.

Standardisation

Remplacement des valeurs manquantes ou aberrantes​

Création de nouvelles variables​

Transformation des variables​

Discrétisation des variables quantitatives​

Numérisation des variables discrètes​

L'encodage one-hot​

Normalisation & Standardisation​