Statistique univariée

L'analyse statistique univariée est une étape fastidieuse mais nécessaire afin de nous assurer de sélectionner les bonnes variables et identifier certaines lacunes qui pourraient être corrigées.

Dans un projet data, il est commun de réaliser un rapport sur chaque source de données. L'objectif est double : il permet de conscientiser l'initiateur du projet sur les lacunes des données disponibles et par conséquent certaines limites pour les modèles qui seront réalisés ainsi qu'identifier les processus à modifier afin de pouvoir garantir dans le futur une meilleure qualité des données à disposition.

L’analyse statistique univariée consiste à :

• Analyser le taux de remplissage de chaque variable ;
• Détecter d’éventuelles anomalies dans la distribution des variables ( valeurs extrêmes ou incongrues ) ;
• Identifier les variables ( champs ) obsolètes ou redondants ;
• Se mettre quelques ordres de grandeur en tête ( âge moyen, revenus moyens,… ) ;
• Identifier les classes pour la discrétisation d’une variable continue ;
• ...

L'occasion se présente pour nous de faire un rappel sur les notions de base en statistique qui sont primordiales et utilisées dans le processus d'implémentation d'un algorithme.

Dispersion des données

L'écart-type et la variance sont deux mesures étroitement liées qui quantifient la dispersion - la répartition dans l'espace - de chaque enregistrement ( individus ) autour de la moyenne. La variance est une étape nous permettant de calculer l'écart-type, fortement utilisé par un data scientist car cette mesure permet de standardiser les données dans le processus de préparation des données, c'est à dire de mettre l'ensemble des données sur une même échelle afin d'éviter qu'une variable apporte un biais au modèle de part justement cette différence d'échelle ; mais également pour rendre le modèle plus efficient - notamment en terme de rapidité - lors des phases d'entrainement ou d'application.

Prenons l'exemple d'une classe de $20$ étudiants ayant passé un examen dans une branche des sciences des données. Sur $20$ étudiants, $10$ ont obtenu une cote de $6/20$ et $10$ ont obtenu une cote de $18/20$. Si nous souhaitons calculer la moyenne de la classe. Nous devons procéder comme suit :

Moyenne

Calcul de la moyenne : la moyenne est la somme des valeurs de la variable divisée par le nombre d'individus. Moyenne = $\frac{\sum_{i}^n x_i}{n}$. Dans le cas présenté ci-dessus, notre moyenne serait de $\frac{(10*6)+(18*6)}{20} = 12$ soit 12/20 de moyenne. Or, cela ne reflète pas vraiment la réalité qui est que la moitié des étudiants sont bien en-dessous de la moyenne et l'autre moitié des étudiants sont bien au-dessus de la moyenne.

📝 La moyenne est un indicateur permettant de mesurer ( et résumer ) une distribution de valeurs en un nombre réel. La moyenne n'est pas impactée par l'ordre des valeurs

$\frac{\sum_{i}^n x_i}{n}$

import pandas as pd
moyenne = df['valeurs'].mean()

import numpy as np
moyenne = np.mean(df['valeurs'])

Dans le cas présent, la meilleure façon de mettre en avant cette information et d'identifier à quel point les valeurs varient par rapport à la moyenne, c'est à dire de comprendre quels sont les écarts par rapport à cette moyenne.

Calcul de l'écart par rapport à la moyenne $= x_i - \bar{x}$. Dans notre exemple, pour les étudiants ayant eu un mauvais résultat, l'écart correspond -6 ( la moyenne étant de 12 et ils ont tous obtenu 6 ) et pour les étudiants ayant eu un excellent résultat, l'écart correspond à +6 ( la moyenne étant de 12 et ils ont tous obtenu 18 ).

Variance

attention

Le problème est le suivant : si nous décidons de calculer la moyenne de ces écarts nous obtiendrons 0 : $\frac{10 x (-6) + (10 x 6)}{(10 + 10)} = \frac{(-60 + 60)}{20} = 0$ ! Or, ce n'est pas correct !

La variance : pour corriger cela, il suffit d'annuler le sigle positif ou négatif en calculant le carré - c'est à dire de calculer l'écart au carré par rapport à la moyenne $σ² = (∑ (xᵢ - \bar{x})² ) / n$ , de sorte que nous obtiendrons : $\frac{10 \times (-6)^2 + 10 \times 6^2}{10 + 10} = \frac{360 + 360}{20} = \frac{720}{20} = 36$.

📝 La variance est une mesure de la dispersion des valeurs d'une variable. Elle correspond à la moyenne des carrés des écarts à la moyenne et est toujours positive.

$\sigma^2 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n}$.

Les librairies pandas & numpy nous permettent de calculer la variance :

import pandas as pd
variance = df['valeurs'].var()

import numpy as np
variance = np.var(df['valeurs'])

Écart-type

Cette étape nous a permis d'annuler les signes positifs et négatifs. Le souci, c'est qu'à la base nous souhaitons calculer l'écart et non l'écart au carré.

Calcul de l'écart-type : pour cela, il nous suffit de calculer la racine carrée des écarts au carré, ce qui correspond à l'écart-type. Dans notre exemple cela reviendrait à calculer $\sqrt{36} = 6$.

📝 L'écart type est - tout comme la variance - une mesure de la dispersion des valeurs d'une variable et se définit comme étant la racine carrée de la variance -. L'écart-type permet de calculer l'écart moyen et plus sa valeur est faible, plus les enregistrements sont considérés comme homogènes.

$\sigma = \sqrt{\frac{\sum_{i=1}^{N} (x_i - \bar{x} )^2}{N}}$.

import pandas as pd
ecart_type = df['valeurs'].std()

import numpy as np
ecart_type = np.std(df['valeurs'])

Étendue

L'étendue nous donne une idée des valeurs minimales et maximales de notre variable.

Calcul de l'étendue : $Max(x) - Min(x)$. Prenons l'exemple de l'âge des patients d'un hôpital. Si nous calculons l'étendue nous devrions obtenir un âge allant de 0 (min) à 120 ans (max). L'étendue pourrait nous permettre d'identifier un patient dont l'âge est de 822 ans ! en réalité, il s'agit peut-être simplement de 82 avec une faute de frappe mais comme le logiciel permet d'intégrer une valeur à 3 chiffes, l'encodage a été validé. Cet encodage doit absolument être corrigé pour l'utilisation de techniques en statistique dans le but de créer un modèle d'apprentissage.

L'étendue est utile pour le data scientist s'il souhaite utiliser la normalisation min-max pour mettre toutes les variables sur une même échelle

astuce

bien que la standardisation soit préférée car le normalisation Min-Max suppose que les données sont distribuées sous forme gaussienne.

📝 L'étendue est également une mesure de dispersion qui évalue la différence entre la valeur maximale et la valeur minimale d'une distribution de donnée

$Max(x) - Min(x)$

import pandas as pd
étendue = df['valeurs'].max() - df['valeurs'].min() 

import numpy as np
étendue = np.max(df['valeurs']) - np.min(df['valeurs'])

Médiane

La médiane est la valeur centrale qui partage l’échantillon en deux groupes de mêmes effectifs : 50% au-dessus ; 50 % en-dessous. ( ! Les valeurs doivent être ordonnées ).

Calcul de la mediane : Tri par ordre croissant des données & identification de la valeur qui sépare l'échantillon en son milieu.

• Si le nombre d'observations n est impair, la médiane est simplement la valeur qui sépare les enregistrement en deux ( partie de gauche nombre pair, partie de droite nombre pair ).
• Si le nombre d’observations n est pair, la médiane est la demi-somme des termes de rang $n/2$ et $(n/2)+1$.

Exemple 1 : nombre d'observations impair : la médiane de $[1,👉4👈,7]$ est $4$ car elle divise les enregistrements en deux : $(n+1)/2$ soit $(3+1)/2$ = la $2e$ valeur $4$ ;

Exemple 2 : nombre d'observations pair : la médiane de $[1,4,8,(👉👈)10,12,14]$ est $9$ car le nombre d’enregistrement est pair et par conséquent on tient compte de la demi-somme entre les valeurs $n/2 = 6/2 = 3e$ valeur soit $8$ et $(n/2)+1 = (6/2)+1 = 4e$ valeur soit $10$ et nous faisons la demi-somme soit $(8+10)/2 = 9$ ;

La médiane est utile pour le data scientist pour pouvoir calculer par la suite la demie médiane inférieure et la demi médiane supérieure dans le but de pouvoir identifier l'écart-interquartile et donc les valeurs considérées comme aberrantes ( outliers ).

📝 La médiane est une valeur qui sépare les enregistrements de parts égales en deux : la moitié inférieure et la moitié supérieure. ! les valeurs doivent être triées par ordre croissant.

import pandas as pd
médiane = df['valeurs'].median() 

import numpy as np
médiane = np.median(df['valeurs']) 

Mode

Le mode est la valeur de la variable qui revient le plus fréquemment dans la série. C'est la valeur centrale de la classe qui a le plus grand effectif

Calcul du mode : compter le nombre d'occurrence des valeurs dans la variable et sélectionner le valeur dominante. Si nous souhaitons représenter le mode sous forme de graphique, nous pourrions d'une part représenter en tant que dimension, les valeurs de la variable ( par exemple Country ) et d'autre par utiliser une mesure pour calculer le nombre de fréquences de chaque valeur par exemple $Count([Country])$ as Frequencies

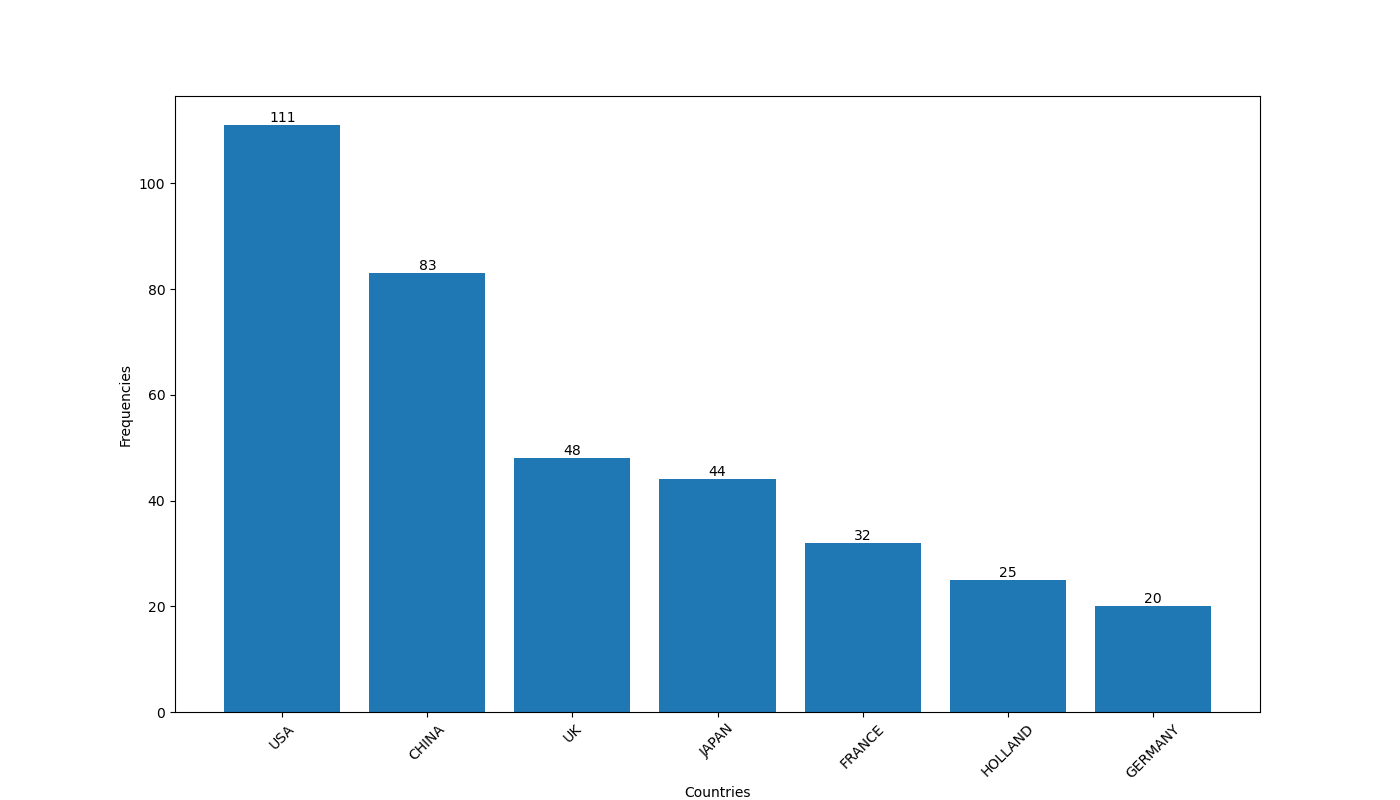
📝 Le mode correspond à la valeur dominante d'une variable, c'est à dire la valeur dont la fréquence est la plus importante.

import pandas as pd
mode = df['valeurs'].mode() 

Écart-interquartile

L'écart-interquartile permet de mettre en avant des données considérées comme étant aberrantes au regard de la distribution des valeurs d'une variable. Dans un exemple précédent, nous avons mentionné qu'il est utile d'utiliser la fonction max ou min pour découvrir des valeurs incohérentes comme par exemple un âge à 822 ans. L'écart-interquartile ( Quartile 3 [Q3] - Quartile 1 [Q1] ) va considérer l'entièreté de la distribution et considérer que toute valeur supérieure à Q3 + (1.5 * Q3-Q1) ( outliers supérieurs ) et toute valeur inférieure Q1 - (1.5 * Q3-Q1 ) ( outliers inférieurs ) doit être écartée des analyses car elle est considérée comme étant abérrante ( outliers ).

Calcul de l'écart-interquartile : pour calculer l'écart-interquartile, nous devons d'abord identifier le quartile 3 (Q3) et le quartile 1 (Q1). Il s'agit des médianes inférieures et supérieure à la médiane. Par conséquent, nous devons dans un premier temps calculer la médiane.

Prenons l'exemple de la série suivante :

$[1,3,5,6,7,7,7,8,8,👉8👈,9,9,9,9,9,10,10,10,10]$ :

• Étape 1 : identification de la médiane. Le nombre de valeurs présent est impair $(19)$ ; Il nous suffit donc de sélectionner la valeur qui va répartir les enregistrements en deux parts égales à savoir $9$ d'un coté et $9$ de l'autre coté. Il s'agit donc de la $10e$ valeur $(N+1)/2$, soit la valeur 8 qui se situe juste avant la valeur 9.


• Étape 2 : identification de la médiane inférieure. Nous nous concentrons donc uniquement sur la série qui se situe en dessous de la médiane $[1,3,5,6,7,7,7,8,8,👉$. Nous avons 9 valeurs donc nous prenons la valeur qui sépare cette sous-série en deux $[1,3,5,6,👉7👈,7,7,8,8,👉$ ; $Q1 = 7$.


• Étape 3 : identification de la médiane supérieure. Nous nous concentrons donc uniquement sur la série qui se situe au dessus de la médiane $👈,9,9,9,9,👉9👈,10,10,10,10]$ . Nous avons 9 valeurs donc nous prenons la valeur qui sépare cette sous-série en deux $👈,9,9,9,9,9,10,10,10,10]$ ; $Q3 = 9.


• Étape 4 : calcul de l'écart-interquartile soit $Q3-Q1$ $= 9-7 = 2$.


• Étape 5 : calcul de la borne outliers supérieure soit $Q3 + 1.5*(Q3-Q1)$ soit $9 + 1.5*(9-7) = 12$. Toutes les valeurs supérieures à 12 devraient donc être écartées si nous souhaitons considérer des valeurs aberrantes pour une seule variable et que pour des besoins propres à l'objectifs, nous souhaitons les écartes.


• Étape 6 : calcul de la borne outliers inférieure soit $Q1 - 1.5*(Q3-Q1)$ soit $7 - 1.5*(9-7) = 4$. Toutes les valeurs inférieures à 12 devraient donc être écartées si nous souhaitons considérer des valeurs aberrantes pour une seule variable et que pour des besoins propres à l'objectifs, nous souhaitons les écartes.

import pandas as pd

Q1 = df['valeurs'].quantile(0.25)
Q3 = df['valeurs'].quantile(0.75)

IQR = Q3 - Q1

print("L'IQR est:", IQR)

import numpy as np

Q1 = np.percentile(f['valeurs'], 25)
Q3 = np.percentile(f['valeurs'], 75)

IQR = Q3 - Q1

print("L'IQR est:", IQR)

📝 L'écart interquartile est une mesure de dispersion autour de la médiane et correspond à la différence entre la demi-médiane supérieure d'une médiane ( Q3 - quartile 3 ) et la demi-médiane inférieure de cette même médiane ( Q1 - Quartile 1 ) ! les valeurs doivent être triées par ordre croissant.

astuce

La librairie pandas propose une fonction à appliquer sur une table de données qui donnera automatiquement la majorité des informations statistiques descriptives de chaque variable ( fréquence, moyenne, écart-type, min, max, Q1, Q3 et médiane ).

import pandas as pd
dataframe.describe()