Univariate Statistics

Univariate statistical analysis is a tedious but necessary step to ensure we select the right variables and identify any shortcomings that could be addressed.

In a data project, it is common to create a report on each data source. The objective is twofold : it helps to raise awareness among the project initiator about the limitations of the available data and, consequently, some constraints on the models that will be created, as well as to identify processes that need to be modified to ensure better data quality in the future.

Univariate statistical analysis involves :

• Analyzing the fill rate of each variable ;
• Detecting any anomalies in the distribution of variables ( extreme or incongruous values ) ;
• Identifying obsolete or redundant variables ( fields ) ;
• Getting a sense of some key figures ( average age, average income,… ) ;
• Identifying classes for discretizing a continuous variable ;
• ...

This is an opportunity to review basic statistical concepts that are essential and used in the process of implementing an algorithm.

Data Dispersion

Standard deviation and variance are two closely related measures that quantify the dispersion - the spread in space - of each record ( individuals ) around the mean. Variance is a step that allows us to calculate the standard deviation, which is widely used by data scientists because this measure helps to standardize the data in the data preparation process. This means putting all the data on the same scale to avoid one variable introducing bias into the model due to this difference in scale ; it also makes the model more efficient - particularly in terms of speed - during training or application phases.

Let’s take the example of a class of $20$ students who took an exam in a data science subject. Out of $20$ students, $10$ scored $6/20$, and $10$ scored $18/20$. If we want to calculate the class average, we should proceed as follows :

Mean

Calculation of the mean : the mean is the sum of the values of the variable divided by the number of individuals. Mean = $\frac{\sum_{i}^n x_i}{n}$. In the example above, our mean would be $\frac{(10*6)+(18*6)}{20} = 12$, meaning an average of $12/20$. However, this does not truly reflect the reality that half of the students are well below the average and the other half are well above the average.

📝 The mean is an indicator that measures ( and summarizes ) a distribution of values into a single real number. The mean is not affected by the order of values.

$\frac{\sum_{i}^n x_i}{n}$

import pandas as pd
mean = df['values'].mean()

import numpy as np
mean = np.mean(df['values'])

In this case, the best way to highlight this information and identify how much the values vary from the mean is to understand the deviations from this mean.

Calculation of the deviation from the mean $= x_i - \bar{x}$. In our example, for students who scored poorly, the deviation is -6 ( the mean being 12 and they all scored 6 ), and for students who scored excellently, the deviation is +6 ( the mean being 12 and they all scored 18 ).

Variance

warning

The problem is as follows : if we decide to calculate the mean of these deviations, we will get 0 : $\frac{10 x (-6) + (10 x 6)}{(10 + 10)} = \frac{(-60 + 60)}{20} = 0$ ! But this is not correct !

Variance : to correct this, we simply need to eliminate the positive or negative sign by squaring the deviation - that is, calculating the squared deviation from the mean $σ² = (∑ (xᵢ - \bar{x})² ) / n$ so that we obtain : $\frac{10 \times (-6)^2 + 10 \times 6^2}{10 + 10} = \frac{360 + 360}{20} = \frac{720}{20} = 36$.

📝 Variance is a measure of the dispersion of values of a variable. It corresponds to the mean of the squared deviations from the mean and is always positive.

$\sigma^2 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n}$.

The pandas & numpy libraries allow us to calculate variance :

import pandas as pd
variance = df['values'].var()

import numpy as np
variance = np.var(df['values'])

Standard Deviation

This step allowed us to eliminate the positive and negative signs. However, the issue is that our original goal was to calculate the deviation, not the squared deviation.

Calculation of the standard deviation : to do this, we simply need to calculate the square root of the squared deviations, which corresponds to the standard deviation. In our example, this would be $\sqrt{36} = 6$.

📝 The standard deviation, like variance, is a measure of the dispersion of values of a variable and is defined as the square root of the variance. The standard deviation allows us to calculate the average deviation, and the smaller its value, the more homogeneous the records are considered.

$\sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n}}$.

import pandas as pd
Standard_Deviation = df['values'].std()

import numpy as np
Standard_Deviation = np.std(df['values'])

Range

The range gives us an idea of the minimum and maximum values of our variable.

Calculation of the range : $Max(x) - Min(x)$. Let's take the example of the age of patients in a hospital. If we calculate the range, we might get an age range from 0 ( min ) to 120 years ( max ). The range could help us identify a patient whose age is recorded as 822 years ! In reality, this might simply be 82 with a typographical error, but since the software allows for a three-digit value, the entry was accepted. This entry must be corrected for the use of statistical techniques to create a learning model.

The range is useful for the data scientist if they wish to use min-max normalization to put all variables on the same scale.

tip

Although standardization is preferred, as min-max normalization assumes that the data is distributed in a Gaussian form.

📝 The range is also a measure of dispersion that evaluates the difference between the maximum and minimum values in a data distribution.

$Max(x) - Min(x)$

import pandas as pd
range = df['values'].max() - df['values'].min() 

import numpy as np
range = np.max(df['valeurs']) - np.min(df['values'])

Median

The median is the central value that divides the sample into two groups of equal size : $50$ above and $50$ below. ( ! Values must be ordered ).

Calculation of the median : sort the data in ascending order & identify the value that splits the sample in the middle.

• If the number of observations is odd, the median is simply the value that separates the records into two equal parts ( even number on the left side, even number on the right side ).
• If the number of observations is even, the median is the average of the two middle terms, ranked $n$ and $n+1$.

Example 1 : odd number of observations : the median of $[1,👉4👈,7]$ is $4$ because it divides the records into two : $(n+1)/2$ or $(3+1)/2$ = the $2^{nd}$ value $4$ ;

Example 2 : even number of observations : the median of $[1,4,8,(👉👈)10,12,14]$ is $9$ because the number of records is even, and therefore we take into account the average of the values $n/2 = 6/2 = 3^{rd}$ value $8$ and $(n/2)+1 = (6/2)+1 = 4^{th}$ value $10$, and we calculate the average : $(8+10)/2 = 9$.

The median is useful for the data scientist to subsequently calculate the lower and upper half-median, which helps to identify the interquartile range and, therefore, the values considered as outliers.

📝 The median is a value that splits the records into two equal parts : the lower half and the upper half. ! Values must be sorted in ascending order.

import pandas as pd
median = df['values'].median() 

import numpy as np
median = np.median(df['values']) 

Mode

The mode is the value of the variable that occurs most frequently in the series. It is the central value of the class with the largest frequency.

Calculation of the mode : count the number of occurrences of each value in the variable and select the dominant value. If we want to represent the mode in a graph, we could, on one hand, represent the values of the variable as a dimension ( for example, Country ) and, on the other hand, use a measure to calculate the frequency of each value, such as $Count([Country])$ as Frequencies.

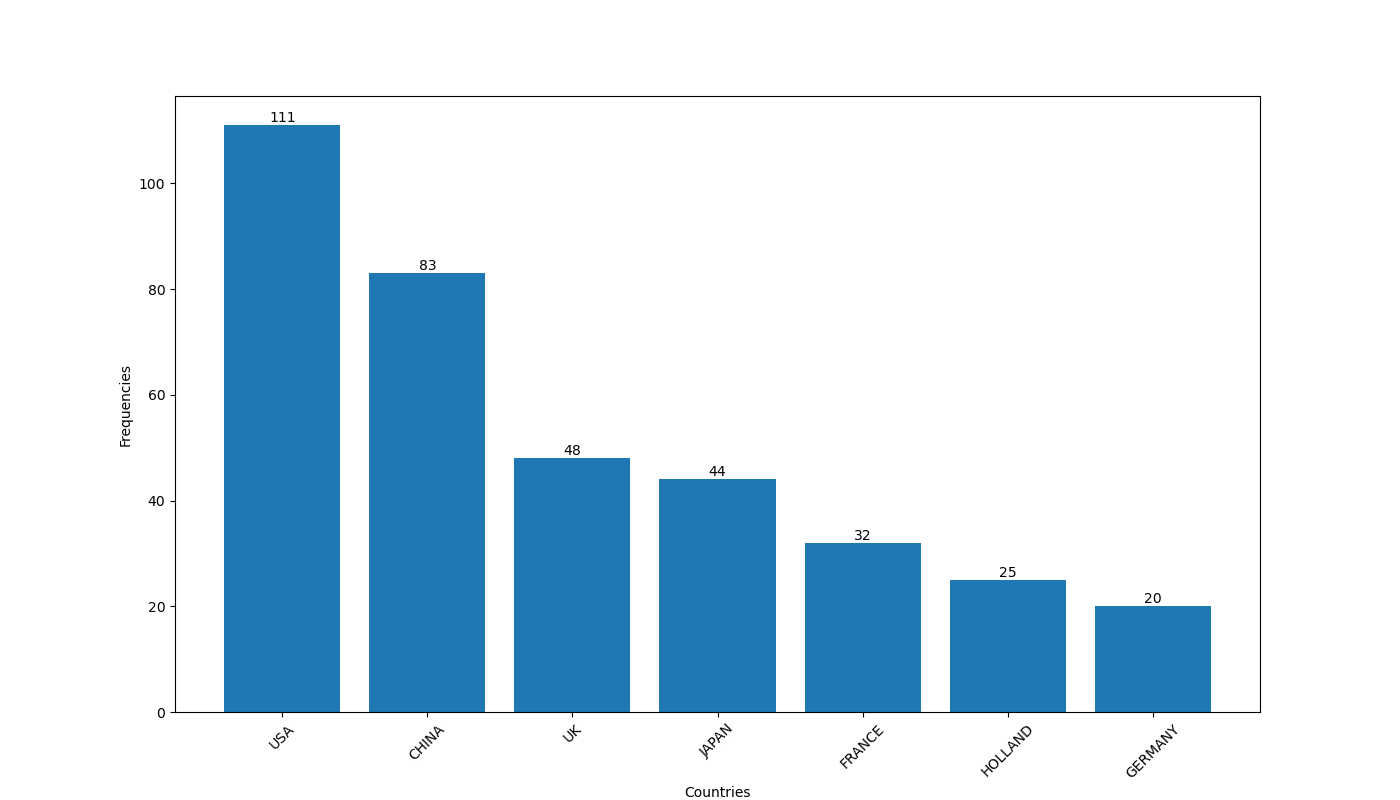
📝 The mode corresponds to the dominant value of a variable, meaning the value with the highest frequency.

import pandas as pd
mode = df['values'].mode() 

Interquartile Range (IQR)

The interquartile range ( IQR ) helps to identify data considered as outliers in the distribution of a variable's values. In a previous example, we mentioned that it is useful to use the max or min function to discover inconsistent values, such as an age of $822$ years. The IQR ( quartile 3 [Q3] - quartile 1 [Q1] ) considers the entire distribution and determines that any value greater than Q3 + (1.5 * (Q3-Q1)) ( upper outliers ) and any value less than Q1 - (1.5 * (Q3-Q1)) ( lower outliers ) should be excluded from analyses as they are considered outliers.

Calculation of the interquartile range : to calculate the IQR, we first need to identify the third quartile ( Q3 ) and the first quartile ( Q1 ). These are the medians of the lower and upper halves of the data, respectively. Therefore, we must first calculate the median.

Let’s take the following series as an example :

$[1,3,5,6,7,7,7,8,8,👉8👈,9,9,9,9,9,10,10,10,10]$

• Step 1 : identify the median. The number of values is odd $(19)$; so we simply select the value that splits the records into two equal parts, with $9$ on one side and $9$ on the other. This is the $10^{th}$ value $(N+1)/2$, which is $8$, located just before the value $9$.


• Step 2 : identify the lower median. We focus only on the series below the median $[1,3,5,6,7,7,7,8,8,👉$. We have 9 values, so we take the value that splits this subset in two $[1,3,5,6,👉7👈,7,7,8,8,👉$; $Q1 = 7$.


• Step 3 : identify the upper median. We focus only on the series above the median $👈,9,9,9,9,👉9👈,10,10,10,10]$. We have 9 values, so we take the value that splits this subset in two $👈,9,9,9,9,9,10,10,10,10]$; $Q3 = 9$.


• Step 4 : calculate the interquartile range, which is $Q3-Q1$ $= 9-7 = 2$.


• Step 5 : calculate the upper outlier threshold, which is $Q3 + 1.5*(Q3-Q1)$ or $9 + 1.5*(9-7) = 12$. Any values greater than 12 should be excluded if we want to consider outliers for a single variable and wish to exclude them for the specific objectives.


• Step 6 : calculate the lower outlier threshold, which is $Q1 - 1.5*(Q3-Q1)$ or $7 - 1.5*(9-7) = 4$. Any values less than 4 should be excluded if we want to consider outliers for a single variable and wish to exclude them for the specific objectives.

import pandas as pd

Q1 = df['values'].quantile(0.25)
Q3 = df['values'].quantile(0.75)

IQR = Q3 - Q1

print("L'IQR est:", IQR)

import numpy as np

Q1 = np.percentile(f['values'], 25)
Q3 = np.percentile(f['values'], 75)

IQR = Q3 - Q1

print("L'IQR is :", IQR)

📝 The interquartile range is a measure of dispersion around the median and corresponds to the difference between the upper half-median of a median ( Q3 - third quartile ) and the lower half-median of that same median ( Q1 - first quartile ). ! Values must be sorted in ascending order.

tip

The pandas library offers a function that can be applied to a data table, which will automatically provide most of the descriptive statistical information for each variable ( frequency, mean, standard deviation, min, max, Q1, Q3, and median ).

import pandas as pd
dataframe.describe()

:::