KNN Plus proches voisins

La technique des voisins les plus proches ( K-NN Nearest Neighbors ) est une technique supervisée non paramétrique hautement automatisée et qui peut être utilisée pour :

• Le classement : variable catégorique attribuée au nouvel enregistrement sur base du vote des valeurs les plus récurrentes parmi les voisins les plus proches
• La prédiction : variable continue qui est définie sur base de la moyenne (pondérée) des valeurs des plus proches voisins

Cette technique se base sur le concept de similarité, soit d’identifier des enregistrements similaires dans le set de données pour attribuer une valeur manquante d’un enregistrement sur base des valeurs de ses voisins les plus proches

Principes de base

« Si un animal se déplace comme un canard et cancane comme un canard, alors c’est probablement un canard ! ».

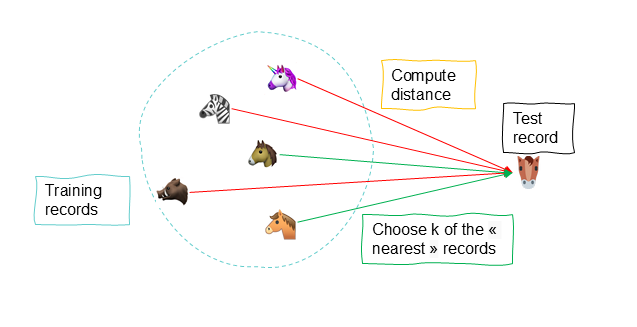
On identifie les $k$ enregistrements les plus similaires (proches voisins) sur base de prédicteurs communs et d’un calcul de distance des valeurs, ce qui va nous permettre d’attribuer au nouvel enregistrement la variable cible $( y_i )$ sur base des valeurs existantes $( y_n )$ des plus proches voisins

Contrairement à la régression linéaire, l’algorithme k-NN est une méthode qui ne prend pas en considération d’éventuelles formes de relation entre la variable cible $( 𝑦 )$ et les prédicteurs $x_[𝑖1],x_[𝑖2],.. x_[ip]$. Ce n’est pas une méthode paramétrique car elle n’implique pas l’estimation de paramètres pour définir une forme de fonction assumée comme c’est le cas pour la forme linéaire de la régression linéaire. Au lieu de cela, cette méthode tire des informations de similitudes entre les valeurs de prédicteurs des enregistrements de l’ensemble des données.

Prenons l'exemple suivant de données sur des voitures.

Prix	Age	Puissance	Poids	Km	Taxe €	Diesel	Essence
13.500	23	90	1165	46.986	210	1	0
14.950	26	90	1170	48.000	224	1	0
22.950	30	150	1220	34.000	150	0	1
12.950	32	80	1050	?	215	1	0

Les données ne contiennent pas de valeur pour le kilométrage pour le quartrième enregistrement. La méthode des K-NN ( K-Nearest Neighbors ) va rechercher, sur base des prédicteurs ( autre variables communes ) et d’un calcul de distance, les k enregistrements similaires ( les voisins ) dont on connait les valeurs de la variables cible ( KM ). Sur base de ces informations et en appliquant une moyenne pondérée, nous pouvons prédire le kilométrage de ce véhicule.

Lorsque l'on parle de similarité en data, il s'agit toujours de la proximité soit le calcule de distance d'un enregistrement par rapport à un autre enregistrement. Concrètement, l'algorithme va calculer l'ordre de proximité des enregistrements existants dont on connait la valeur pour KM et l'enregistrement pour lequel nous souhaitons identifier cette valeur.

L'enregistrement pour lequel nous cherchons la valeur km a une valeur de prix de $12.950$. L'algorithme va donc calculer les distance comme suit : distance1 = $\sqrt{(12.950 - 13.500)^²}$ ; distance2 = $\sqrt{(12.950 - 14.950)^²}$ ; etc.

Dans le cadre d’un classement, la méthode est similaire. On identifie également parmi les k enregistrements les plus proches, la valeur dominante de la classe qui est attribuée à l’enregistrement dont l’information est manquante

Prix	Age	Puissance	Poids	Km	Taxe €	Carburant
13.500	23	90	1165	46.986	210	Diesel
14.950	26	90	1170	48.000	224	?
22.950	30	150	1220	34.000	150	Essence
12.950	32	80	1050	47.500	215	Diesel

Notions de distance

Pour pouvoir identifier les voisins les plus proches, cette méthode tire des informations des similitudes entre les valeurs prédictives des enregistrements de l'ensemble de données en tenant compte de la notion de distance. La question centrale est donc de pouvoir mesurer les distances entre les enregistrements sur base des valeurs prédictives. Ce qui rend ces propriétés utiles, c’est le fait qu’une distance bien définie implique que chaque enregistrement a un voisin parmi les autres données.

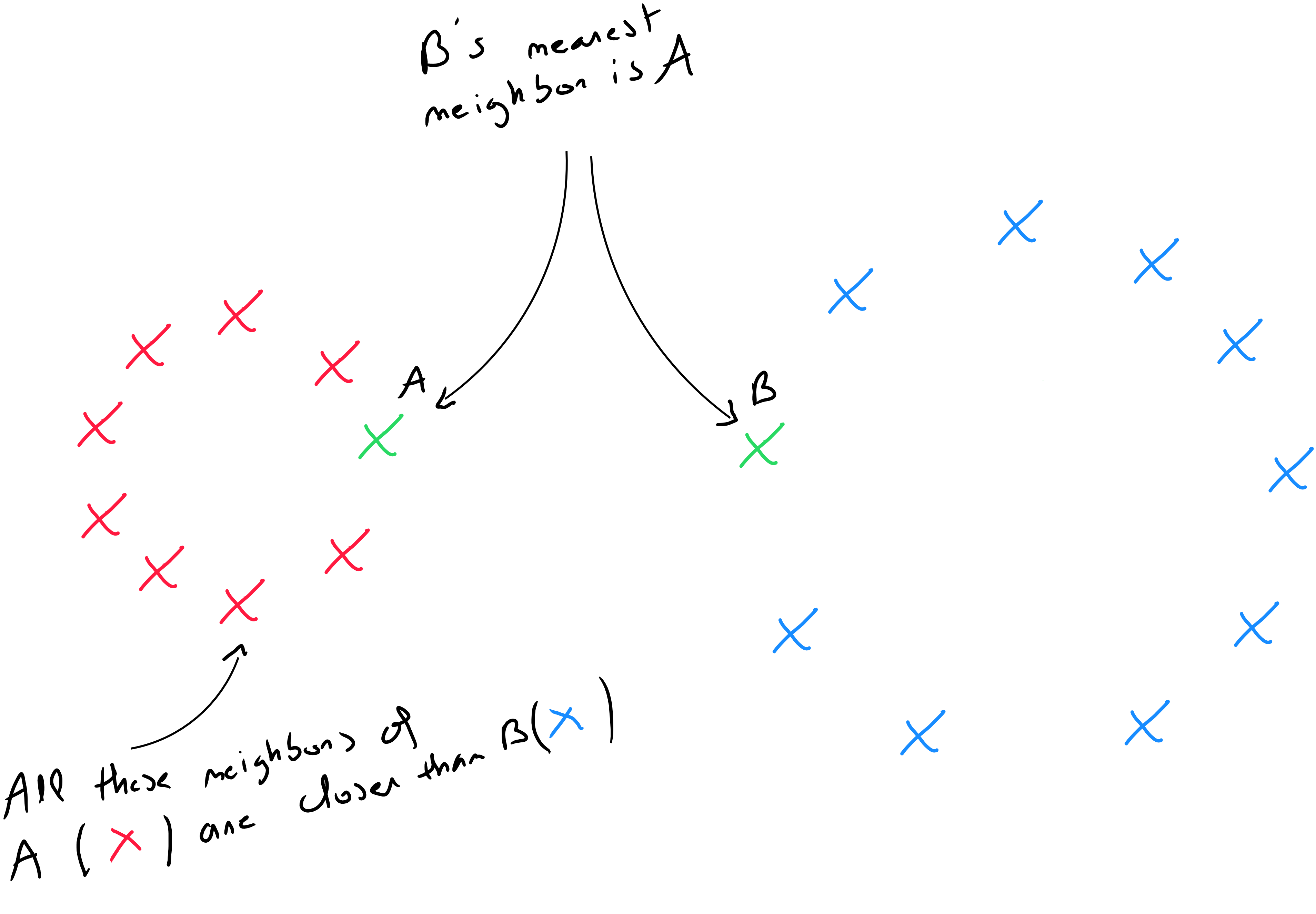
La distance d’un enregistrement par rapport à un autre doit être calculée sur base de l'ensemble des prédicteurs de différents type. Toutefois, une des notions fondamentales et bien entendu de transformer les données pour pouvoir appliquer des calculs de distance. Si les variables sont de type qualitatives ordinales, elle doivent être numérisées. Si les variables sont de type qualitatives nominales, nous devons procéder à un encodage one-hot.

Dans ce cas, la distance sera calculée pour chacun des champs. Prenons l’exemple du set de données suivant qui contient deux variables quantitative et une variable qualitative :

ID	Gender	Age	Salary
1	Female	27	19 000
2	Male	51	64 000
3	Male	52	105 000
4	Female	33	55 000
5	Male	45	45 000

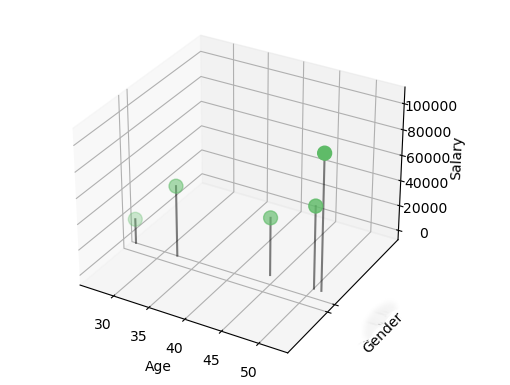
L’illustration dans un scatter plot en trois dimensions nous permet de mieux identifier les distances entre les enregistrements. L’idée est donc de calculer une distance entre toutes les valeurs d’un enregistrement par rapport à toutes les valeurs des autres enregistrements pour définir ensuite sur base d’un seuil, les $k$ voisins les plus proches.

Distance Euclidienne

La distance Euclidienne est celle dont on a le plus souvent recourt pour calculer une distance entre deux enregistrements car elle est considérée comme étant la moins gourmande. Il s'agit simplement de la distance la plus directe entre un point A et un point B.

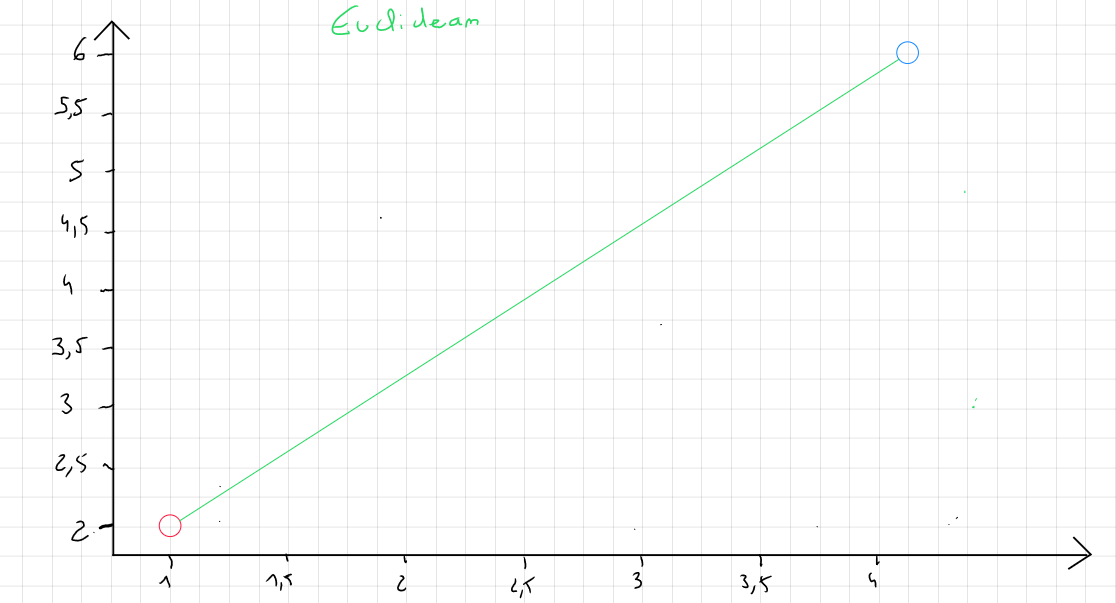
La formule de la distance Euclidienne s'écrit comme suit :

$$d(p, q) = \sqrt{\sum_{i=1}^{n} (p_i - q_i)^2}$$

soit

$$d(p, q) = \sqrt{(p_{i1} - q_{i1})^2 + (p_{i2} - q_{i2})^2 + \dots + (p_{in} - q_{in})^2}$$

Pour l'exemple suivant :

ID	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$x_7$	$x_8$
01	1.06	9.2	151	54.4	1.6	9,077	0	0.628
02	0.89	10.3	202	57.9	2.2	5,088	25.3	1.555

La distance se calcule comme suit :

$$d_{1,2} = \sqrt{(1.06 - 0.89)^2 + (9.2 - 10.3)^2 + (151 - 202)^2 + (54.4 - 57.9)^2 + (1.6 - 2.2)^2 + (9.077 - 5.088)^2 +(0.628 - 1.555)^2 } = 3989.408$$

La distance est calculée pour tous les enregistrement $d_{1,3},d_{1,4},d_{1,...},d_{1,n}$.

La distance Euclédienne est fortement influencée par l'échelle de chaque variable. Il est donc d'usage de normaliser les données pour les convertir sur une même échelle. En outre, elle ne tient pas compte d'éventuelles relations entre les variables ( corrélation ) et est sensible aux outliers.

Distance Manhattan

Si les données contiennent des outliers et que pour des raisons x ou y, ces outliers ne sont pas retirés, on préconisera la mesure de la distance Manhattan qui se concentre sur la valeur absolue des différences plutôt que le carré des différences.

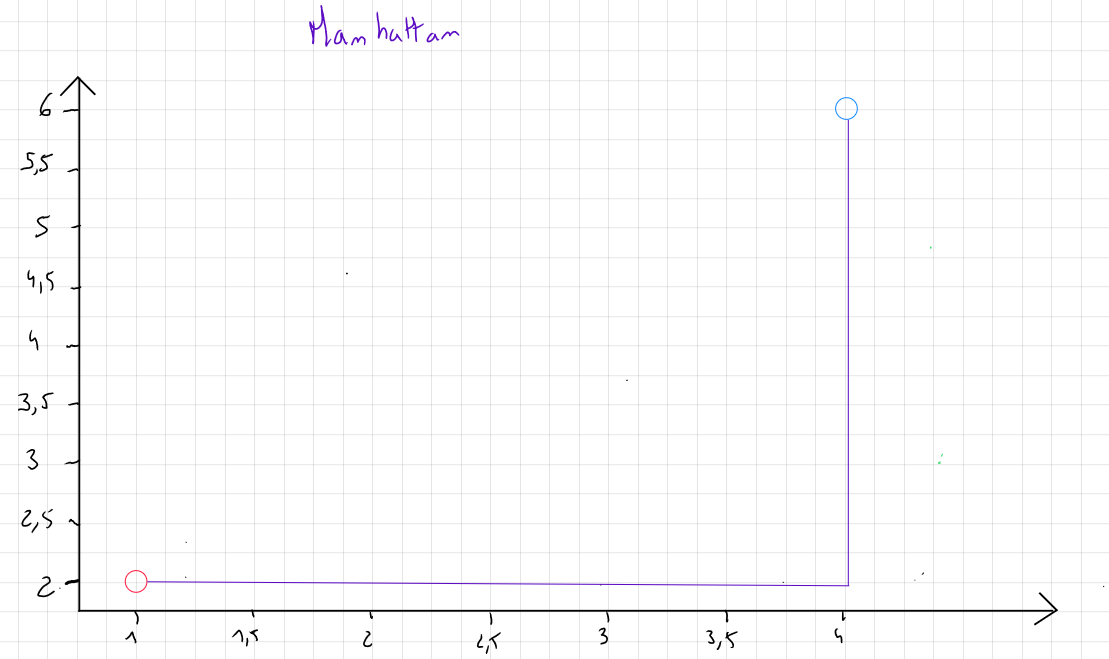
Cette mesure porte ce nom car elle correspond en deux dimensions à la distance parcourue par un taxi dans les rues de Manhattan, qui sont toutes soit parallèles soient perpendiculaires les unes aux autres

La formule de la distance Manhattan s'écrit comme suit :

$$d(p, q) = \sum_{i=1}^{n} |p_i - q_i|$$

soit

$$d(p, q) = |p_{i1} - q_{i1}| + |p_{i2} - q_{i2}| + \dots + |p_{in} - q_{in}|$$

Pour l'exemple suivant :

ID	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$x_7$	$x_8$
01	1.06	9.2	151	54.4	1.6	9,077	0	0.628
02	0.89	10.3	202	57.9	2.2	5,088	25.3	1.555

La distance se calcule comme suit :

$$d_{1,2} = |1.06 - 0.89| + |9.2 - 10.3| + |151 - 202| + |54.4 - 57.9| + |1.6 - 2.2| + |9.077 - 5.088| +|0.628 - 1.555| = 61.286$$

La distance est calculée pour tous les enregistrement $d_{1,3},d_{1,4},d_{1,...},d_{1,n}$

Distance Minkowski

La distance Minkowski est une mesure de distance qui généralise les distances Euclidienne et Manhattan.

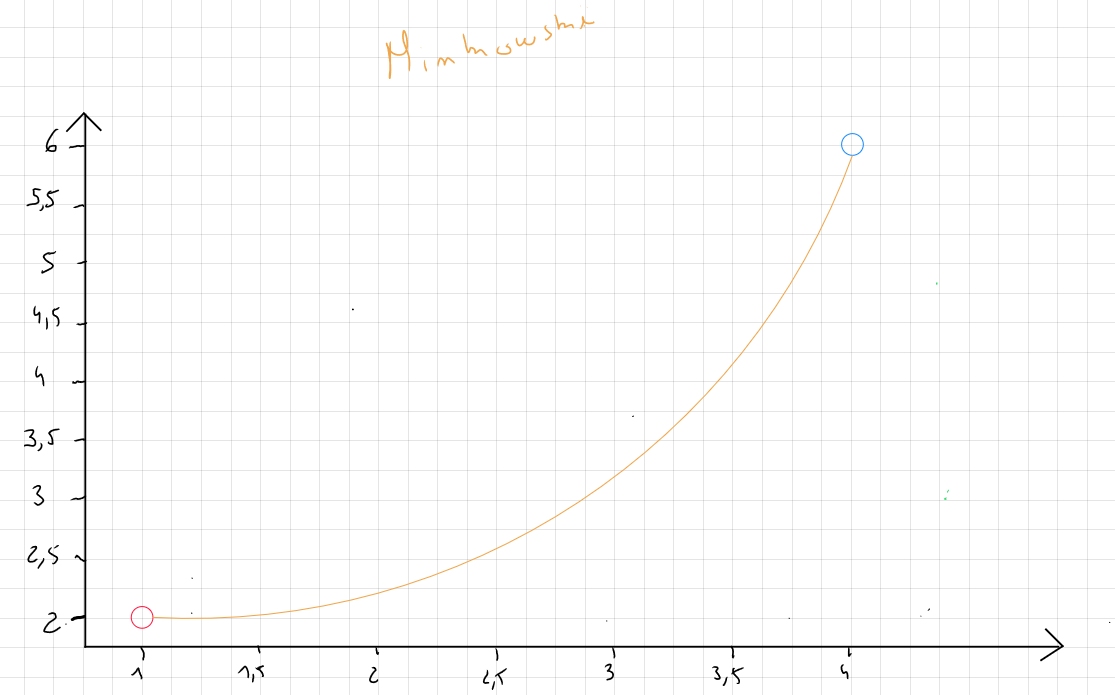
La formule de la distance Minkowski s'écrit comme suit :

$$d(p, q) = \left( \sum_{i=1}^{n} |p_i - q_i|^p \right)^{\frac{1}{p}}$$

soit

$$d(p, q) = (|p_{i1} - q_{i1}| + |p_{i2} - q_{i2}| + \dots + |p_{in} - q_{in}|)^\frac{1}{3}$$

P correspond au paramètre de puissance qui contrôle la façon dont les différences entre les coordonnées des points sont agrégées. Ce paramètre peut prendre plusieurs valeurs mais la littérature mais en avant comme pratique courante le choix $p =1$ qui correspond en fait à appliquer la distance Manhattan ; le choix $p =2$ qui correspond à appliquer la distance Euclidienne et des valeurs de $p > 2$ qui est plus sensible aux grandes différences entre les valeurs.

Concrètement, la distance Minkowski permet de tester plusieurs combinaison par la modification de la valeur p selon les besoins de l'analyste.

Pour l'exemple suivant :

ID	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$x_7$	$x_8$
01	1.06	9.2	151	54.4	1.6	9,077	0	0.628
02	0.89	10.3	202	57.9	2.2	5,088	25.3	1.555

La distance se calcule comme suit :

$$d_{1,2} = (|1.06 - 0.89| + |9.2 - 10.3| + |151 - 202| + |54.4 - 57.9| + |1.6 - 2.2| + |9.077 - 5.088| +|0.628 - 1.555|)^\frac{1}{3} = 3.94$$

La distance est calculée pour tous les enregistrement $d_{1,3},d_{1,4},d_{1,...},d_{1,n}$

Définition de la valeur de K

Le principe des KNN Plus proches voisins est de définir la valeur finale sur base des $k$ voisins les plus proches. Par exemple, Le $3, 4 ou 5$ voisins les plus proches. Toutefois cette valeur n'est pas choisie de manière arbitraire.

Après avoir calculé la distance entre les valeurs d’un enregistrement et les valeurs de tous les enregistrements, nous devons définir une règle pour spécifier à quelle classe appartiendra notre enregistrement (classement) ou quelle est la valeur de notre enregistrement (estimation)

La règle la plus simple et la moins complexe en termes de calculs serait $k = 1$ soit la valeur $y_i$ correspond à la valeur $y$ de l’enregistrement le plus proche. Il s’avère en fait que le taux d’erreur reste très important dans ce cas-là et par convention nous définirons la règle suivante : $k > 1$.

L’idée est donc :

1. De trouver les k-voisins les plus proches de l’enregistrement qui doit être classé ou estimé
2. Définir la valeur sur base d’une règle de la majorité et d’un seuil (classement) ; de la moyenne pondérée des valeurs (prédiction)

De manière générale, Si k est trop important, le modèle risque de s’ajuster au bruit et donc être en sur-apprentissage. Le risque de biais est réduit mais la variance augmente ; Si k est trop faible, on ne pourra pas identifier de structures dans les données, la variance est réduite mais le risque de biais augmente

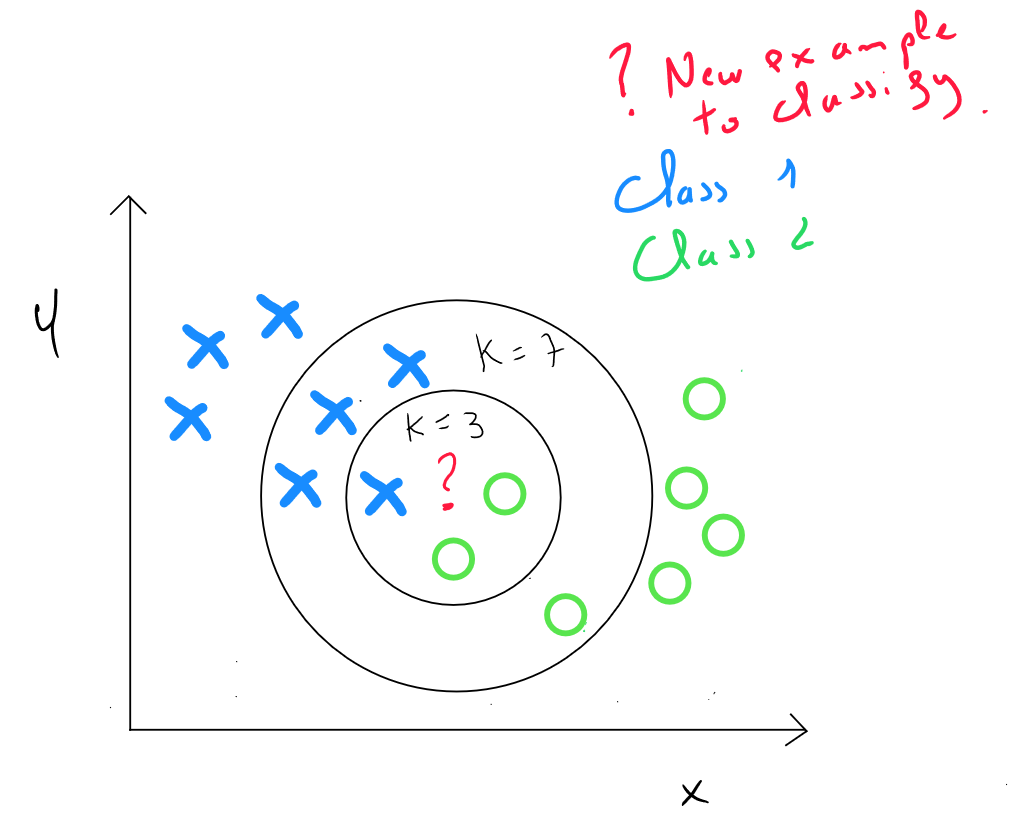
Le choix de $k$ portera sur la valeur $k$ qui minimise les erreurs entre $y$ et $\hat{y}$. KNN étant une technique supervisée, nous utilisons les données d'entrainement qui sont entrainées selon plusieurs scénarios de $k$ ( en général de $2$ à $9$ ) et nous sélectionnerons la valeur de $k$ qui minimise les erreurs du modèle.

L’objectif est donc de sélectionner $k$ qui représente la meilleure performance de classement ou d’estimation :

1. Dans le cadre d’un classement, après avoir entrainé notre modèle, on applique les connaissances du modèle dans le set de validation et on calcule le taux de précision, soit la correspondance entre les prédictions et le réel (matrice de confusion)
2. Dans le cadre d’une prédiction, on réalise la même opération mais on calcule ensuite la racine carrée de l’erreur quadratique moyen (RMSE = √("MSE" )) et on sélectionne le $k$ qui minimise cette somme

Définition de ŷ

L'algorithme fera donc un ensemble d'itération sur les données d'entrainement en définissant différents valeurs de $k$ afin de pouvoir identifier $k$ qui minimise les erreurs=; Lorsque l'on connait la valeur de $k$, nous devons encore définir une règle pour identifier la classe ou estimer la valeur.

Classement

Pour un classement, la définition de la majorité est directement liée à la notion de seuil. Imaginons que pour $k = 4$,$$3 valeurs = ‘riche’, $1$ valeur = ‘pauvre’. Dans ce cas, notre nouvel enregistrement correspondra à ‘riche’ car la probabilité que la valeur corresponde à riche est de $75$ contre $25$ pour ‘pauvre’. Nous définirons en général un seuil de $50$ pour maximiser la précision.

Estimation

Dans le cadre d’une estimation, on tiendra compte de toutes les valeurs des voisins les plus proches et l’on calculera la valeur prédite sur base de la moyenne pondérée des valeurs des voisins. La pondération sera appliquée sur base de la notion de distance :

$$\frac{\sum_{i=1}^{n} w_i * x_i}{\sum_{i=1}^{n} w_i} \text{ où } w_i = \frac{1}{d_i} \text{ (} d_i \text{ = l'inverse de la distance)}$$

Code Python KNN Estimation

import pandas as pd
from sklearn.datasets import fetch_california_housing


housing = fetch_california_housing(as_frame=True)


x = housing.data    #Predictors
y = housing.target  #House Price 

# Combining in a dataframe to display
data = pd.concat([x, y], axis=1)


data

# MedInc  = median income of households
# HouseAge = age of the house
# AveRooms = the average number of rooms per house
# AveRooms = the average number of bedrooms per house
# Population = the total population in area
# AveOccup =The average number of occupants per house
# Latitude
# Longitude
# MedHouseVal = Price (measured in hundreds of thousands of dollars

# Import libraries
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt

# Step 1: Split data into Train + Validation (60%) and Test (40%)
x_train_full, x_test, y_train_full, y_test = train_test_split(
    x, y, test_size=0.4, random_state=42
)

# Step 2: Split Train + Validation into Train (60%) and Validation (20% of total data)
x_train, x_val, y_train, y_val = train_test_split(
    x_train_full, y_train_full, test_size=0.25, random_state=42  # 0.25 x 0.6 = 0.15
)

# Step 3: Scale the data (KNN is distance-based and sensitive to scale)
scaler = MinMaxScaler()
x_train_scaled = scaler.fit_transform(x_train)  # Fit on train data
x_val_scaled = scaler.transform(x_val)  # Transform validation data
x_test_scaled = scaler.transform(x_test)  # Transform test data

# Step 4: Hyperparameter tuning using validation set
k_values = range(1, 21)
rmse_values = []  # Store RMSE for each k

for k in k_values:
    # Train the model with k neighbors
    knn_regressor = KNeighborsRegressor(n_neighbors=k)
    knn_regressor.fit(x_train_scaled, y_train)  # Train on training data
    
    # Validate the model on validation set
    y_pred_val = knn_regressor.predict(x_val_scaled)  # Predict on validation data
    
    # Calculate RMSE (Root Mean Squared Error) for validation set
    mse = mean_squared_error(y_val, y_pred_val)
    rmse = np.sqrt(mse)
    rmse_values.append(rmse)
    
    print(f"K={k}, RMSE (Validation)={rmse:.4f}")

# Step 5: Select the best K based on validation performance
best_k = k_values[np.argmin(rmse_values)]
print(f"Best K based on validation set: {best_k}")

# Step 6: Evaluate the final model on the test set
# Train the model with the best K on the training data
knn_regressor_best = KNeighborsRegressor(n_neighbors=best_k)
knn_regressor_best.fit(x_train_scaled, y_train)

# Predict on the test set
y_pred_test = knn_regressor_best.predict(x_test_scaled)

# Calculate RMSE for the test set
mse_test = mean_squared_error(y_test, y_pred_test)
rmse_test = np.sqrt(mse_test)
print(f"RMSE on Test Set (Best K={best_k}): {rmse_test:.4f}")


# Step 7: Visualize RMSE across different K values and include the test performance
plt.figure(figsize=(10, 5))
plt.plot(k_values, rmse_values, marker='o', label="RMSE (Validation)")
plt.axhline(y=rmse_test, color='r', linestyle='--', label=f"RMSE (Test) = {rmse_test:.4f}")
plt.title("KNN Regression: RMSE for Different K Values")
plt.xlabel("Number of Neighbors (K)")
plt.ylabel("RMSE")
plt.legend()
plt.grid()
plt.show()

# Step 8: Add a new data point for prediction
new_record = pd.DataFrame({
    'MedInc': [8.0],  # Median income
    'HouseAge': [30],  # Median house age
    'AveRooms': [6.0],  # Average number of rooms
    'AveBedrms': [1.0],  # Average number of bedrooms
    'Population': [500],  # Total population
    'AveOccup': [3.0],  # Average number of occupants per household
    'Latitude': [34.0],  # Latitude
    'Longitude': [-118.0]  # Longitude
})

# Scale the new data point
new_record_scaled = scaler.transform(new_record)

# Predict the house value for the new data point
new_prediction = knn_regressor_best.predict(new_record_scaled)
print(f"Predicted house value for the new record: €{new_prediction[0] * 100000:.2f}")

knn_regressor = KNeighborsRegressor(n_neighbors=best_k)
knn_regressor.fit(x_train_scaled, y_train)

new_x = np.array([[0.2, 0.5]])  # Example new X value (after scaling)
new_x_scaled = scaler.transform(new_x)
new_y_pred = knn_regressor.predict(new_x_scaled)
print(f"Predicted Y for new x={new_x} is {new_y_pred[0]:.4f}")

Code Python KNN Classement

# Load the Digits dataset
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
import pandas as pd

digits = load_digits()

# Features:
# Each sample has 64 features, representing the pixel intensities of an 8x8 grayscale image.
# Feature values range from 0 (white) to 16 (black).
x = digits.data  # Features (64 features per sample)

# Target:
# The target variable (y) represents the digit label (0 to 9).
y = digits.target  # Target labels (integers from 0 to 9)

# Shape:
# The dataset contains 1,797 samples and 64 features.
print(f"Shape of Features (x): {x.shape}")  # (1797, 64)
print(f"Shape of Target (y): {y.shape}")    # (1797,)

# Visualization:
# Each digit can be visualized as an 8x8 image.
# Below, we visualize the first sample in the dataset.
sample_index = 1  # Index of the digit to visualize
plt.figure(figsize=(4, 4))
plt.imshow(digits.images[sample_index], cmap="gray")  # Visualize the 8x8 image
plt.title(f"Digit Label: {digits.target[sample_index]}")  # Display the target label
plt.axis("off")
plt.show()

# Convert to DataFrame for easier exploration
# Each column represents a pixel (pixel_0 to pixel_63).
# The target column represents the digit label (0 to 9).
data = pd.DataFrame(x, columns=[f'pixel_{i}' for i in range(64)])
data['target'] = y  # Add the target column
print("First 5 rows of the dataset:")
print(data.head())  # Display the first 5 rows

# Import libraries
import numpy as np
import pandas as pd
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns


# Step 1: Split data into Train + Validation (60%) and Test (40%)
x_train_full, x_test, y_train_full, y_test = train_test_split(
    x, y, test_size=0.4, random_state=42
)

# Step 2: Split Train + Validation into Train (60%) and Validation (20% of total data)
x_train, x_val, y_train, y_val = train_test_split(
    x_train_full, y_train_full, test_size=0.25, random_state=42  # 0.25 x 0.6 = 0.15
)

# Step 3: Scale the data
scaler = MinMaxScaler()
x_train_scaled = scaler.fit_transform(x_train)
x_val_scaled = scaler.transform(x_val)
x_test_scaled = scaler.transform(x_test)

# Step 4: Hyperparameter tuning using validation set
k_values = range(1, 21)
accuracy_values = []

for k in k_values:
    knn_classifier = KNeighborsClassifier(n_neighbors=k)
    knn_classifier.fit(x_train_scaled, y_train)
    y_pred_val = knn_classifier.predict(x_val_scaled)
    accuracy = accuracy_score(y_val, y_pred_val)
    accuracy_values.append(accuracy)
    print(f"K={k}, Accuracy (Validation)={accuracy:.4f}")

# Step 5: Select the best K based on validation performance
best_k = k_values[np.argmax(accuracy_values)]
print(f"Best K based on validation set: {best_k}")

# Step 6: Evaluate the final model on the test set
knn_classifier_best = KNeighborsClassifier(n_neighbors=best_k)
knn_classifier_best.fit(x_train_scaled, y_train)
y_pred_test = knn_classifier_best.predict(x_test_scaled)

# Calculate Accuracy for the test set
accuracy_test = accuracy_score(y_test, y_pred_test)
print(f"Accuracy on Test Set (Best K={best_k}): {accuracy_test:.4f}")


# Step 7: Visualize Accuracy across different K values
plt.figure(figsize=(10, 5))
plt.plot(k_values, accuracy_values, marker='o', label="Accuracy (Validation)")
plt.title("KNN Classification: Accuracy for Different K Values (Digits Dataset)")
plt.xlabel("Number of Neighbors (K)")
plt.ylabel("Accuracy")
plt.axhline(y=accuracy_test, color='r', linestyle='--', label=f"Test Accuracy (K={best_k}) = {accuracy_test:.4f}")
plt.legend()
plt.grid()
plt.show()

# Step 8: Predict a new data point
# Create a new data point (an example 8x8 image)
# The pixel values should range between 0 and 16.
new_data = np.array([
    0, 0, 10, 14, 8, 1, 0, 0,
    0, 2, 16, 14, 6, 1, 0, 0,
    0, 0, 15, 15, 8, 15, 0, 0,
    0, 0, 5, 16, 16, 10, 0, 0,
    0, 0, 12, 16, 16, 12, 0, 0,
    0, 4, 16, 6, 4, 16, 6, 0,
    0, 8, 16, 10, 8, 16, 8, 0,
    0, 1, 8, 12, 12, 13, 1, 0
]).reshape(1, -1)  # Reshape to match the input shape (1, 64)

# Scale the new data point using the same scaler
new_data_scaled = scaler.transform(new_data)

# Predict the class for the new data point
new_prediction = knn_classifier_best.predict(new_data_scaled)
predicted_label = new_prediction[0]  # Predicted digit label

print(f"Predicted digit for the new data point: {predicted_label}")

# Visualize the new data point
plt.figure(figsize=(4, 4))
plt.imshow(new_data.reshape(8, 8), cmap="gray")  # Reshape to 8x8 for visualization
plt.title(f"Predicted Label: {predicted_label}")
plt.axis("off")
plt.show()