Clustering

La classification automatique, également connue sous les appellations segmentation ou clustering, est la plus répandue des techniques d’apprentissage non supervisé.

Elle est utilisée lorsqu’on dispose d’un grand volume de données au sein duquel on cherche à distinguer des sous-ensembles homogènes, susceptibles de traitements et d’analyses différenciés.

Il s’agit donc d’une technique non supervisée qui est souvent utilisée en amont (pré-processing) d’une technique supervisée afin d’améliorer les performances de prédiction.

Pour rappel, nous retrouvons deux types d'apprentissages : supervisé et non supervisé. Jusqu'à présent, nous avons abordé des techniques supervisées, c'est à dire des techniques à partir desquelles nous réalisons des prédictions ( classement ou estimation ).

attention

Bien que le terme « classement » se traduit « classification » en anglais et est une technique supervisée ; le terme « classification » en français se traduit par « clustering » en anglais.

• Clustering (EN) − Classification (FR) : découper l’ensemble entier des données en sous-groupes relativement homogènes dans lesquels la similarité des enregistrements dans le groupe est maximisée et la similarité en dehors du groupe est minimisée.
• Classification (EN) – Classement (FR) : placer chaque enregistrement dans une classe, parmi plusieurs classes prédéfinies, en fonction des caractéristiques de l'enregistrement indiquées comme variables explicatives ( prédicteurs ). Le résultat permet d’affecter chaque individu à la meilleure classe.

Comme nous abordons une techniques supervisée, il est important de rappeler une différence fondamentale avec l'apprentissage supervisé : en apprentissage non supervisé, il n'existe que des $x$ ; pas de $y$ et tous les enregistrements sont utilisés - il n'y a pas de partition pour une phase d'entrainement. La technique est appliquée sur l'ensemble des enregistrements et nous devons en tant que data scientist, interpréter le résultat.

Il existe toutefois un lien entre ces deux familles : La plupart des algorithmes prédictifs s’accommodent mal d’un trop grand nombre de variables en raison des corrélations qui existent entre elles et qui perturbent leur pouvoir prédictif. La clustering permet de former des groupes homogènes qui peuvent être décrits par un petit nombre de variables spécifiques à chaque groupe. De plus, il est parfois utile qu’un algorithme prédictif puisse traiter les valeurs manquantes, sans leur substituer des valeurs a priori telles que la moyenne des enregistrements. Une solution consiste à appliquer en amont de cette technique prédictive, une technique de clustering afin de regrouper les individus contenant des valeurs manquantes dans des groupes et imputer la moyenne de ces groupes pour remplacer la valeur manquante.

remarque

Certains schémas et concepts présentés ici sont inspirés du cours Machine Learning d'Andrew Ng, programme créé en collaboration entre Stanford university Online Education et DeepLearning.AI disponible sur Coursera. Retrouvez le cours original ici : Machine Learning by Andrew Ng.

Nous souhaitons donc segmenter une population hétérogène en sous-groupes ou clusters homogènes. Les qualités d’un cluster sont :

• Une forte similarité intra-classe
• Une faible similarité inter-classe

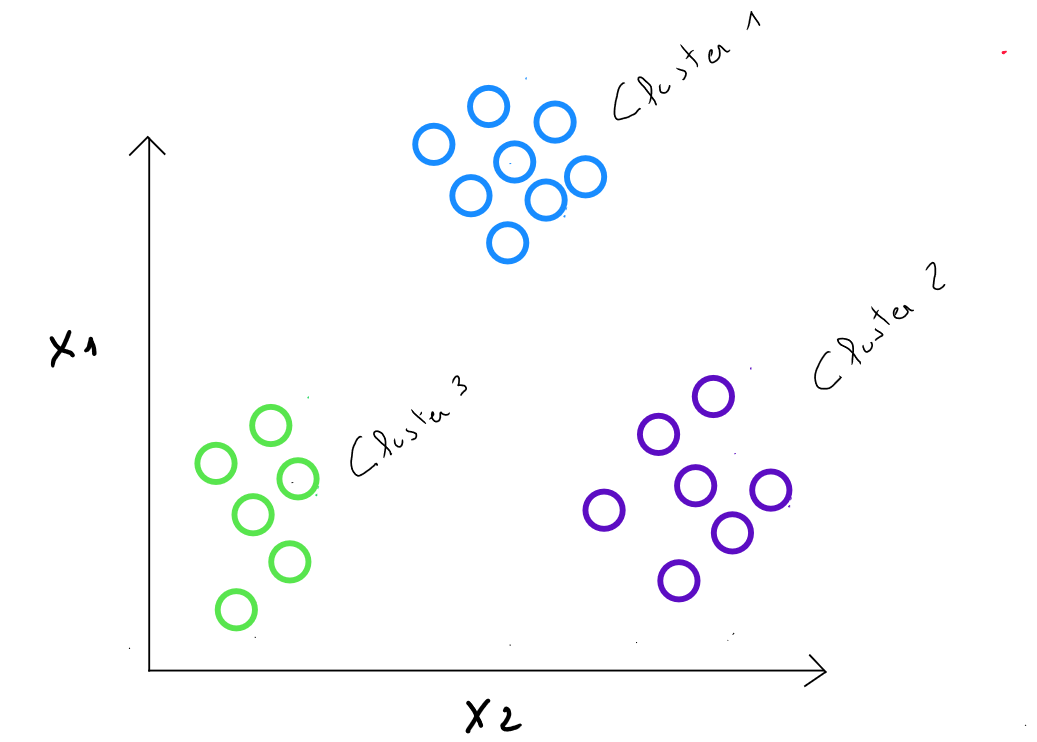
K-means

La méthode des centres mobiles est une des principales méthodes de partitionnement dont l’objectif est de partitionner en différentes classes des individus pour lesquels on dispose de mesures

On cherche à regrouper autant que possible les individus les plus semblables ( du point de vue des mesures que l’on possède ) tout en séparant les classes le mieux possible les unes des autres.

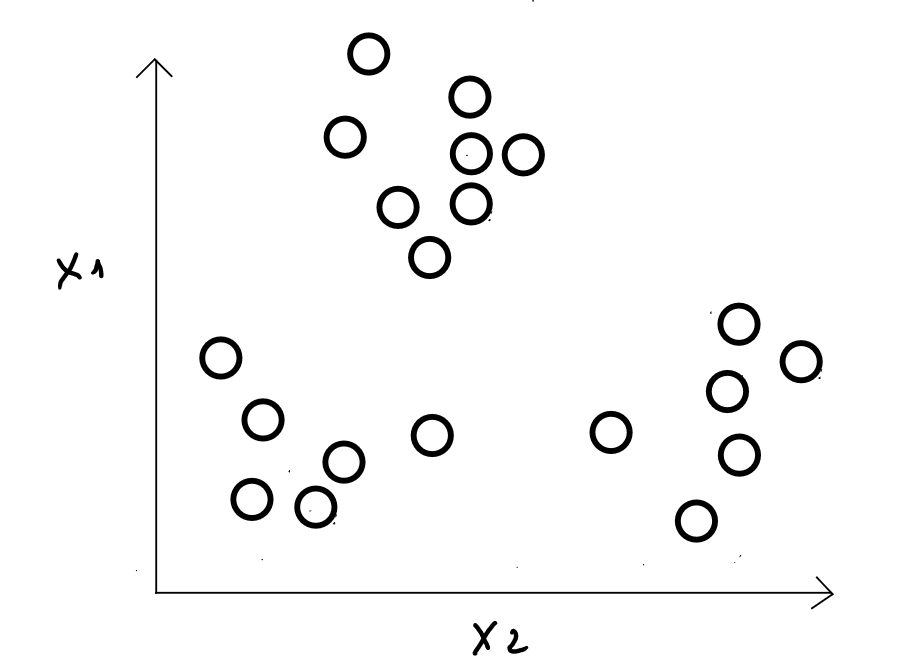
Étapes

À l’étape 1 : on choisit $k$ individus comme centres initiaux des classes ( on définit le nombre de classes et les individus considérés comme étant les centres de ces classes de manière aléatoire ) - en réalité, nous verrons par la suite que l'algorithme « test » de nombreuses configurations pour identifier la meilleure répartition possible des données.

Exemple $k = 3$

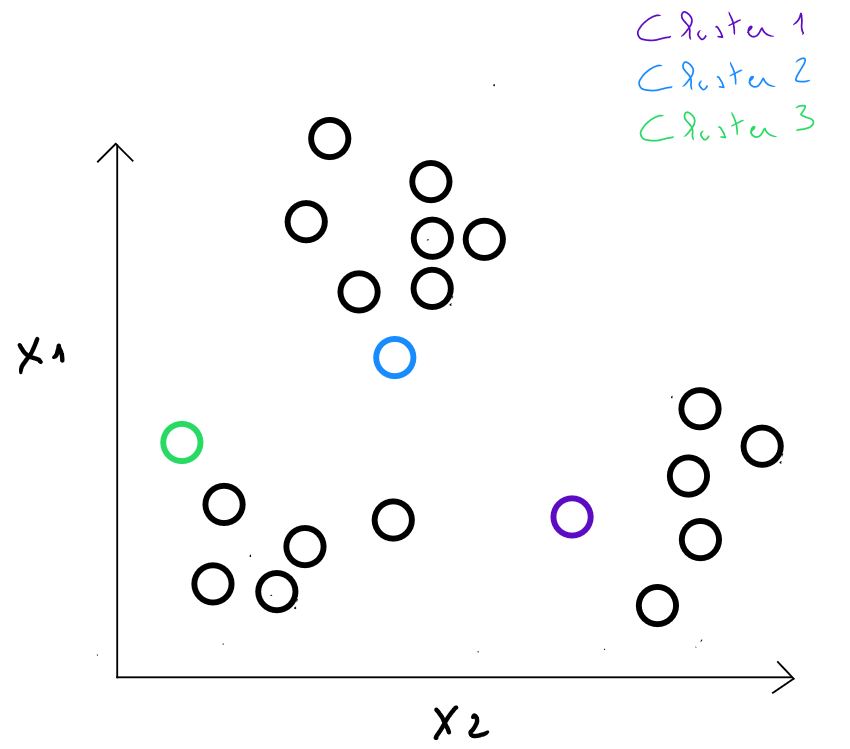
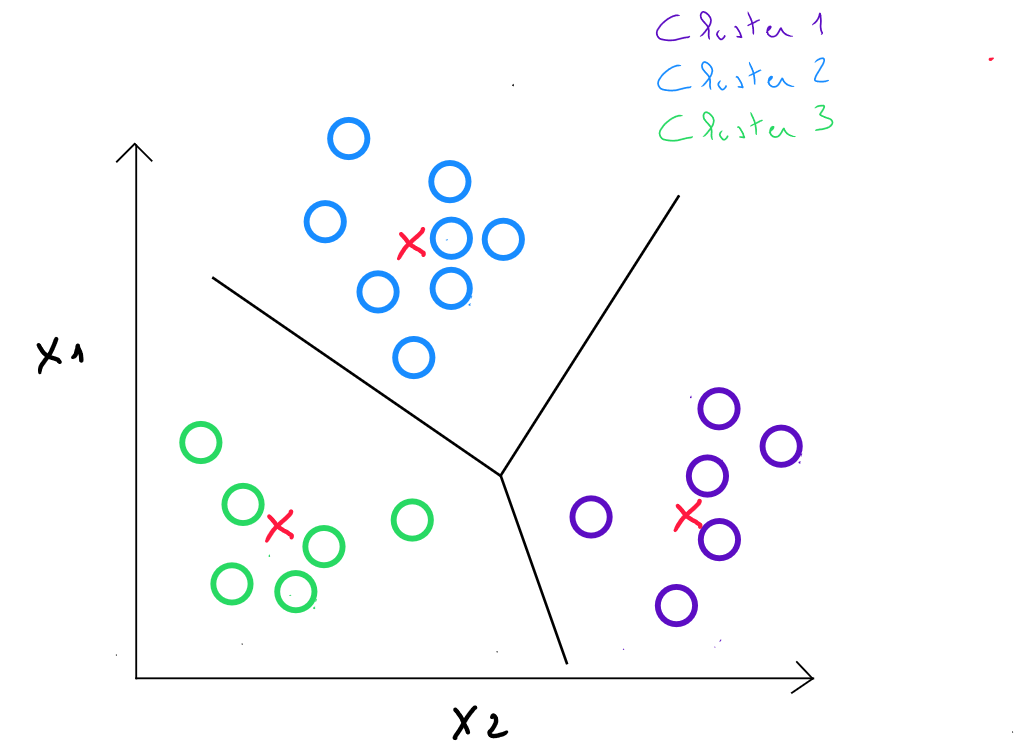
À l’étape 2 : on calcule les distances entre chaque individu et chaque centre de l’étape précédente. On affecte chaque individu au centre le plus proche, ce qui définit k classes

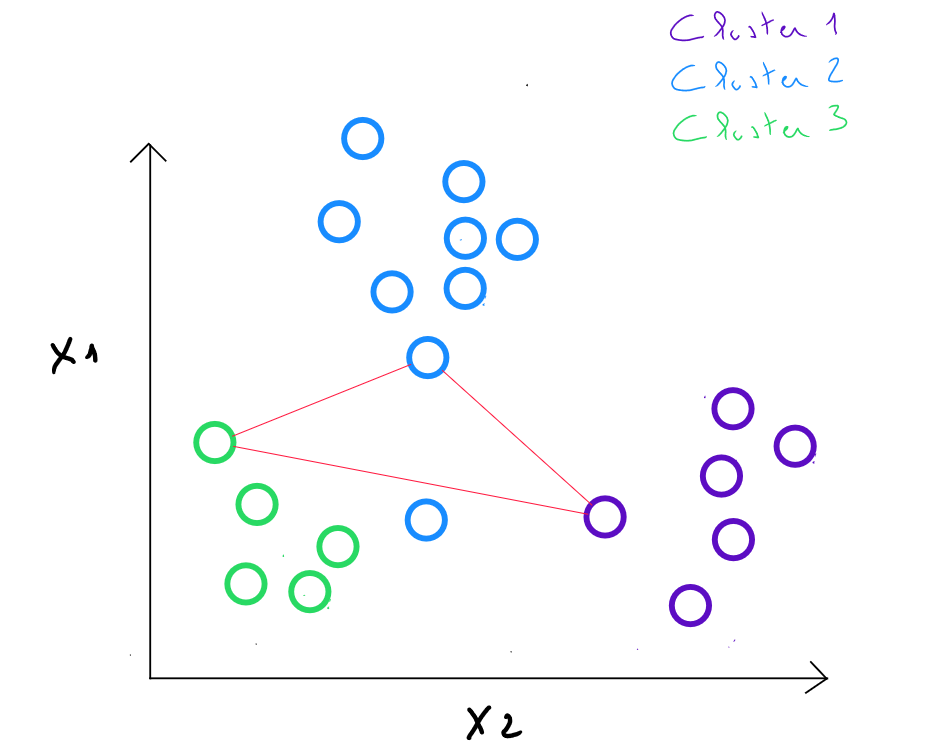
À l’étape 3 : on remplace les centres initiaux des classes par les barycentres des k classes. Les nouveaux centroïdes sont calculés en prenant la moyenne des coordonnées de tous les points appartenant à chaque cluster. ( ces barycentres ne sont pas forcément des valeurs d'enregistrements existants ).

Si par exemple dans le cluster 2 identifié à l'étape $2$, j'obtiens les valeurs $4,6$ et $8$ pour ce cluster ; à l'étape 3, le nouveau centre correspondra à $\frac{4 + 6 + 8}{ 3}$ soit $9$.

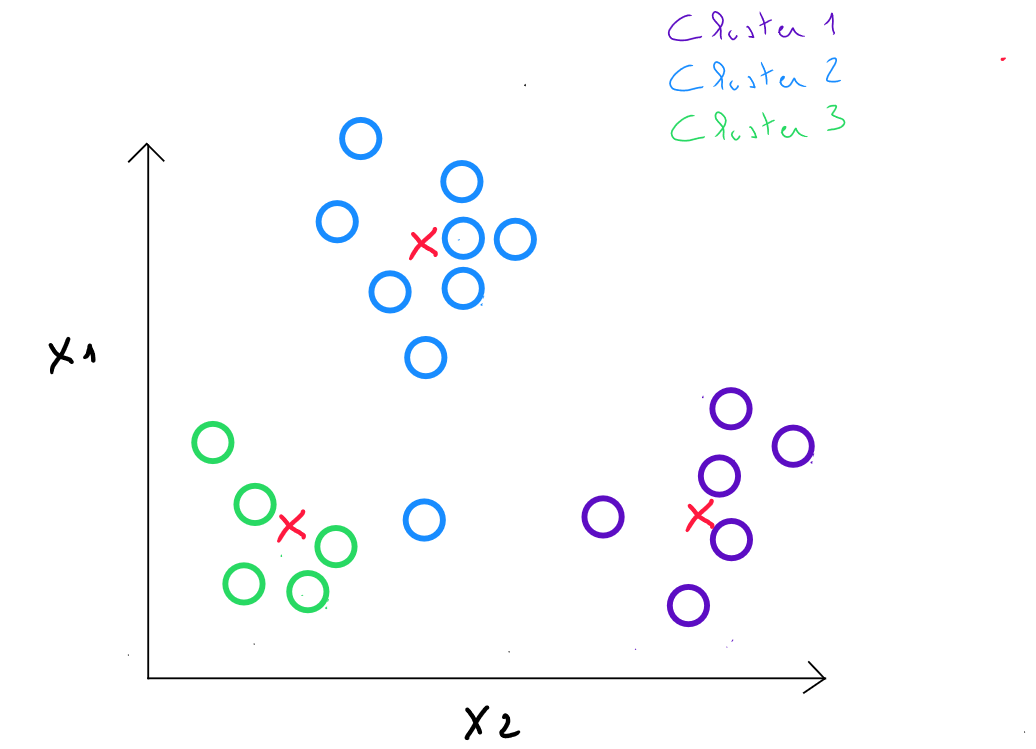
À l’étape 4 : on calcule les distances entre chaque individu et chaque centre et on affecte chaque individu au centre le plus proche.

Les étapes 3 et 4 sont répétées dans des itérations, jusqu’à ce que les centres soient restés suffisamment stables ( en comparant leur déplacement aux distances entre centres initiaux ).

Calcul des distances

Les distances peuvent donc être définies de plusieurs manières mais en général, les propriétés suivantes sont requises :

• Une distance n’est pas négative : $d_{ij} >=0$
• Principe de proximité de soi : $d_{ii} = 0$ ( la distance d’un enregistrement par rapport à lui-même est de 0 )
• Principe de symétrie : $dij = dji$
• Principe du triangle de l’inégalité : $dij <= d_{ik} + d_{kj}$ ( la distance entre n’importe quelle paire ne peut dépasser la somme des distances entre deux autres paires )

Comme nous l'avons dans la technique de K-NN Plus Proches Voisins, la notion de distance entre deux enregistrements ( proximité - similarité ) se calcule sur base de variables quantitatives. Il est donc important dans certains cas de transformer les données pour pouvoir appliquer des calculs de distance. Si les variables sont de type qualitatives ordinales, elle doivent être numérisées. Si les variables sont de type qualitatives nominales, nous devons procéder à un encodage one-hot.

Les trois distances les plus utilisées sont la distance Euclidienne, la distance Manhattan et la distance Minkowski.

Distance Euclidienne

La distance Euclidienne est celle dont on a le plus souvent recourt pour calculer une distance entre deux enregistrements car elle est considérée comme étant la moins gourmande. Il s'agit simplement de la distance la plus directe entre un point A et un point B.

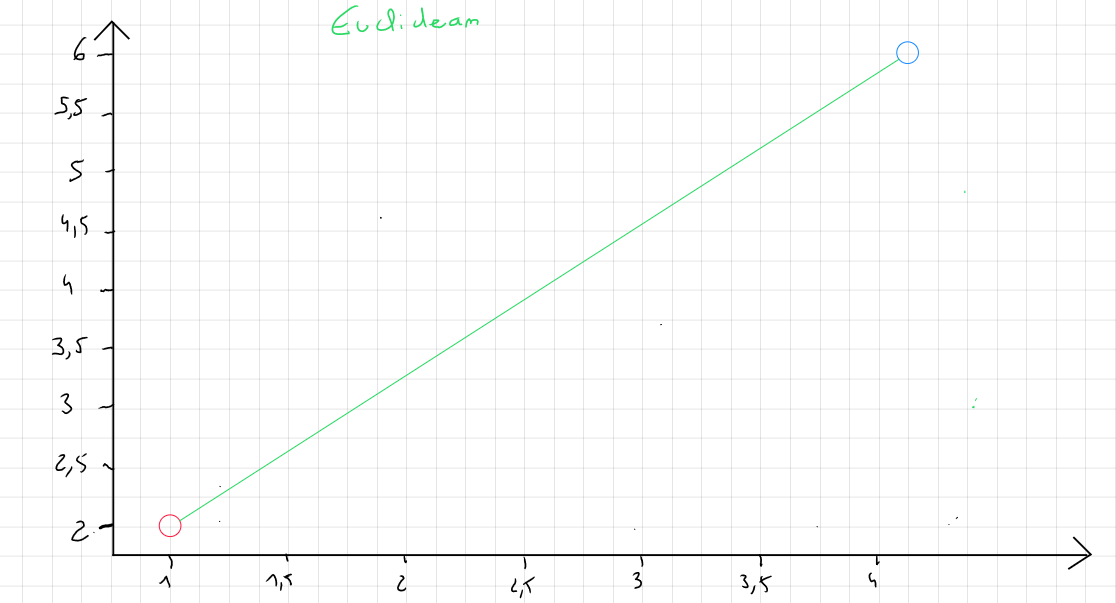
La formule de la distance Euclidienne s'écrit comme suit :

$$d(p, q) = \sqrt{\sum_{i=1}^{n} (p_i - q_i)^2}$$

soit

$$d(p, q) = \sqrt{(p_{i1} - q_{i1})^2 + (p_{i2} - q_{i2})^2 + \dots + (p_{in} - q_{in})^2}$$

Pour l'exemple suivant :

ID	$x_1$	$x_2$
01	2.04	3.2
02	1.98	3.8

La distance se calcule comme suit :

$$d_{1,2} = \sqrt{(2.04 - 1.98)^2 + (3.2 - 3.8)^2} = 0.603$$

La distance est calculée pour tous les enregistrements $d_{1,3},d_{1,4},d_{1,...},d_{1,n}$.

La distance Euclidienne est fortement influencée par l'échelle de chaque variable. Il est donc d'usage de normaliser les données pour les convertir sur une même échelle. En outre, elle ne tient pas compte d'éventuelles relations entre les variables ( corrélation ) et est sensible aux outliers.

Distance Manhattan

Si les données contiennent des outliers et que, pour des raisons spécifiques, ces outliers ne sont pas retirés, nous privilégions la mesure de la distance Manhattan qui se concentre sur la valeur absolue des différences plutôt que le carré des différences.

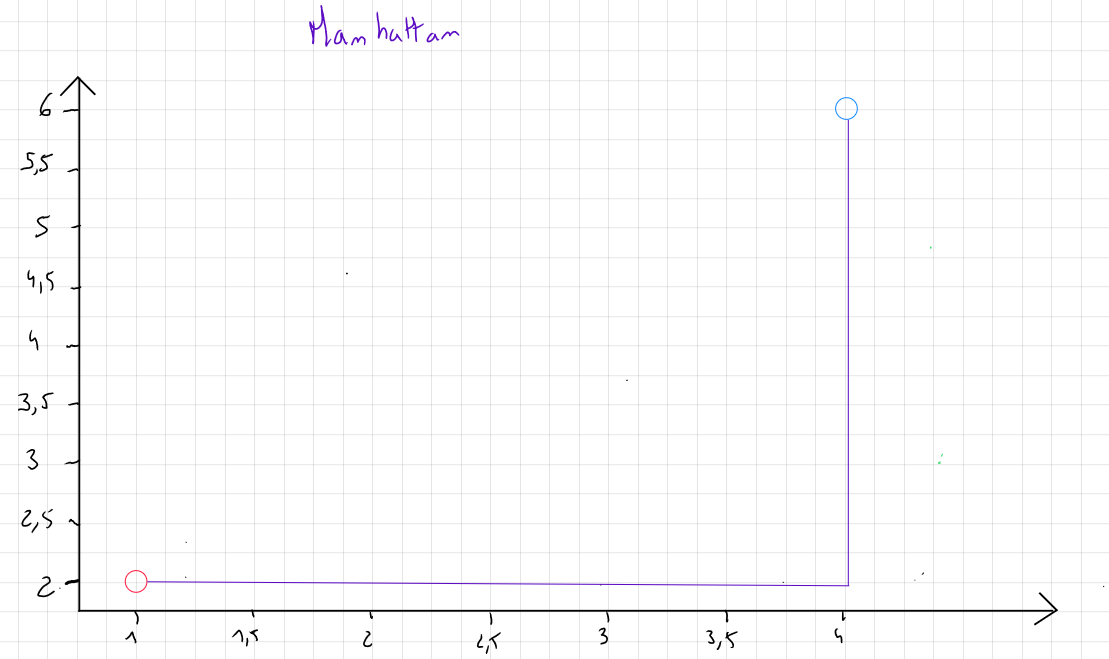
Cette mesure porte ce nom car elle correspond en deux dimensions à la distance parcourue par un taxi dans les rues de Manhattan, qui sont toutes soit parallèles soient perpendiculaires les unes aux autres.

La formule de la distance Manhattan s'écrit comme suit :

$$d(p, q) = \sum_{i=1}^{n} |p_i - q_i|$$

soit

$$d(p, q) = |p_{i1} - q_{i1}| + |p_{i2} - q_{i2}| + \dots + |p_{in} - q_{in}|$$

Pour l'exemple suivant :

ID	$x_1$	$x_2$
01	2.04	3.2
02	1.98	3.8

La distance se calcule comme suit :

$$d_{1,2} = |2.04 - 1.98| + |3.2 - 3.8| = 0.66$$

La distance est calculée pour tous les enregistrement $d_{1,3},d_{1,4},d_{1,...},d_{1,n}$

Distance Minkowski

La distance Minkowski est une mesure de distance qui généralise les distances Euclidienne et Manhattan.

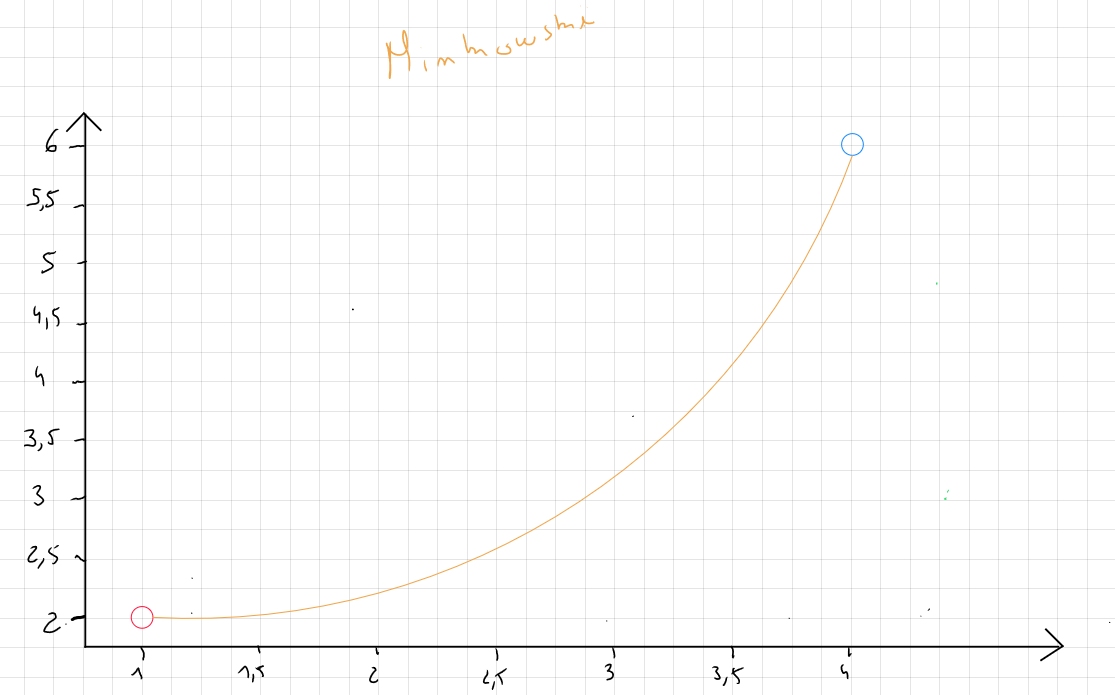
La formule de la distance Minkowski s'écrit comme suit :

$$d(p, q) = \left( \sum_{i=1}^{n} |p_i - q_i|^p \right)^{\frac{1}{p}}$$

soit

$$d(p, q) = (|p_{i1} - q_{i1}| + |p_{i2} - q_{i2}| + \dots + |p_{in} - q_{in}|)^\frac{1}{3}$$

P correspond au paramètre de puissance qui contrôle la façon dont les différences entre les coordonnées des points sont agrégées. Ce paramètre peut prendre plusieurs valeurs mais la littérature mais en avant comme pratique courante le choix $p =1$ qui correspond en fait à appliquer la distance Manhattan ; le choix $p =2$ qui correspond à appliquer la distance Euclidienne et des valeurs de $p > 2$ qui est plus sensible aux grandes différences entre les valeurs.

Concrètement, la distance Minkowski permet de tester plusieurs combinaison par la modification de la valeur p selon les besoins de l'analyste.

Pour l'exemple suivant :

ID	$x_1$	$x_2$
01	2.04	3.2
02	1.98	3.8

La distance se calcule comme suit :

$$d_{1,2} = (|2.06 - 1.98| + |3.2 - 3.8|)^\frac{1}{3} = 0.879$$

La distance est calculée pour tous les enregistrement $d_{1,3}$,$d_{1,4}$,$d_{1,...}$,$d_{1,n}$

Algorithme

Initialisation aléatoire de k centroïdes de clusters $𝜇_1,𝜇_2,…,u_𝑘$
Répétition $[$

1. Assigner les points aux centroïdes des clusters
For $𝑖 =1$ 𝑡𝑜 $𝑚$

$𝑐^1=$ index ( de $1$ à $k$) le centroïde du cluster le plus proche




2. Déplacement des clusters
For $𝑘=1$ 𝑡𝑜 $𝑘$


$𝜇_𝑘=$moyenne des points assignés au cluster $𝑘$
$𝜇_1= \frac{1}{5}*[𝑥^1+𝑥^4+𝑥^7+𝑥^9+𝑥^3]$


$]$

Initiation de k

L’initiation du centre des clusters ainsi que le nombre de clusters est un élément délicat car le choix arbitraire de k ( nombre de clusters ) et l'initiation aléatoire de ces derniers peut donner des clusters différents. C’est la raison pour laquelle lorsque nous sélectionnons k ( exemple $k =3$ ), nous itérons pour différentes initialisations de 3 k parmi les données et sélectionnons le modèle présentant la plus petite fonction de coût.

** ce qui signifie que (1) : l'algorithme va boucler sur différentes valeurs de k pour identifier la meilleure manière de regrouper les données et pour chaque valeur de k, l'algorithme va boucler sur différentes initiations des k.**

Une règle générale est de boucler ( selon le nombre d’exemples ) sur 1 à 100 initialisations différentes par choix de k ( exemple k =3 ) mais cela peut monter de 50 à 1000 pour obtenir un meilleur score.

Fonction coûts

Nous pouvons donc identifier une fonction coût qui cherche à minimiser la variance intra-cluster ( intra-classe ), c'est à dire sélectionner des résultats de groupement de données dans lesquels les données sont les plus proches les unes des autres. Concrètement, cette fonction de coût est calculée pour plusieurs valeurs de $k$. Pour ce faire, pour chaque valeur de $k$, il itérera sur le nombre de clusters et pour chaque cluster sur plusieurs valeurs d'initiations de centroïdes.

Par exemple pour k = 3, l'algorithme réalisera 1 à 100 initiation pour le cluster 1, pour le cluster 2 et pour le cluster 3. Il sélectionnera l'initiation qui minimise la variance intra-clusters ( intra classe ).

$𝐽(𝑐^{(1)},…, 𝑐^{(𝑚)},𝜇_1,…,𝜇_𝑘)=$

La fonction de coût réparti donc les clusters en obtenant l’inertie intra-classe la plus faible.

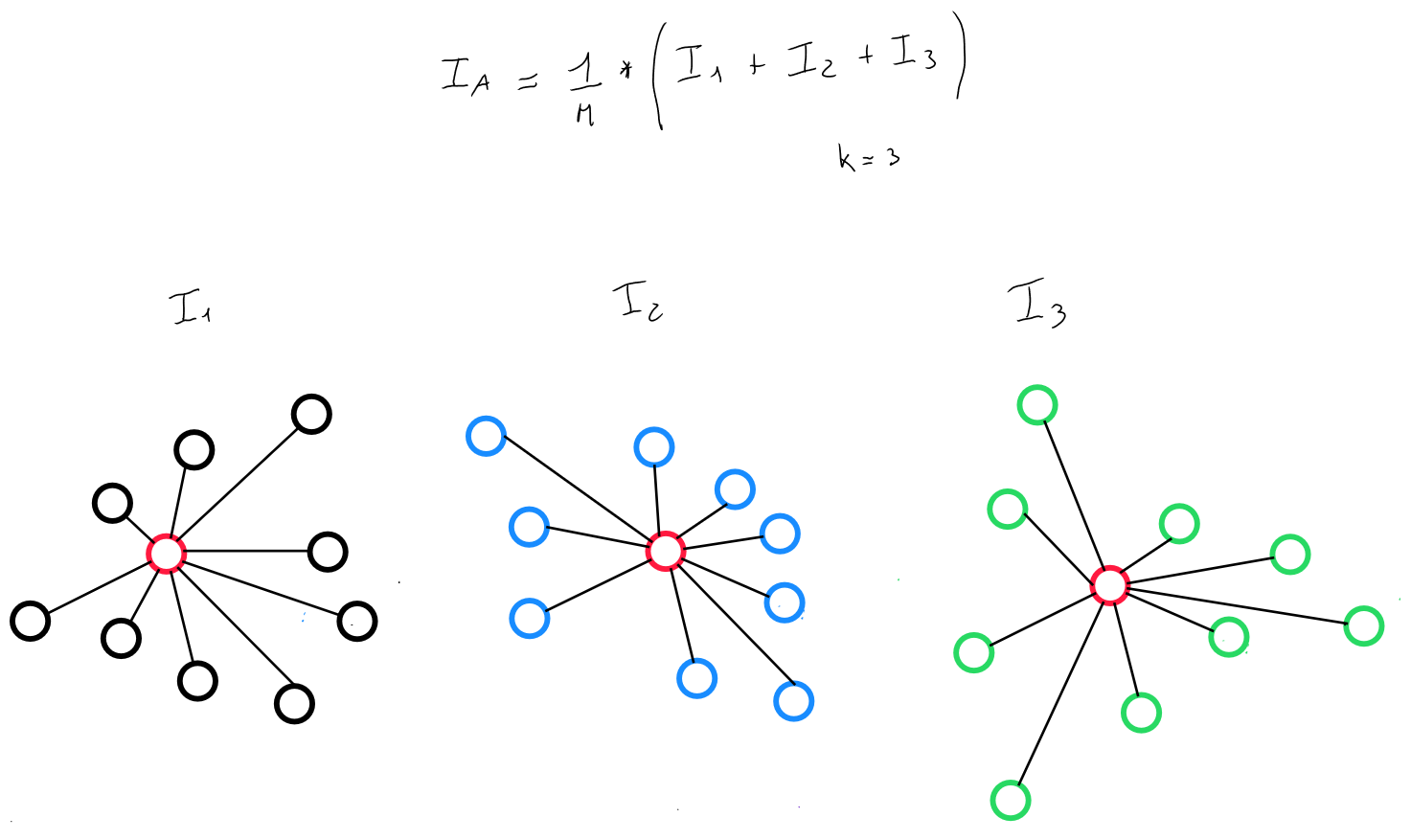
Intertie intra-classe

L’inertie d’un cluster ( classe ) (I_k) est calculée de la même façon, c'est à dire par rapport à son barycentre :

$$\sum_{i \in I} P_i (x_i - \overline{x_j})^2$$

Si la population est segmentée en $k$ clusters, d’inerties $I_1,…,I_𝑘$ , l’inertie intra clusters est, par définition la somme des inerties totales de chaque clusters.

$$Min(I_A) = \frac{1}{m} \sum_{i=1}^{m} \left\| x^{(i)} - \mu_{c^{(1)}} \right\|^2 = J(c^{(1)}, \dots, c^{(m)}, \mu_1, \dots, \mu_k)$$

Sélection de k

Jusqu'à présent, nous avons vu comment minimiser la fonction coût pour des clusters dont le choix de $k$ était arbitraire ( $k = 3$ ). Toutefois, l'objectif est de minimiser la fonction coût pour une technique de cluster à k clusters, sans connaitre à l'avance le nombre de clusters idéal pour la répartition ( segmentation ) de nos données.

De nouveau, l'idée est de réaliser des itérations :

• si $k = 2$, alors on calcul $J(k)$ en réalisant des itérations d'initialisation aléatoire de $k$ ( exemple 1 à 1000 ), car le choix initial des valeurs de k peut impacter le résultat.
pour chaque initiation aléatoire de 2 valeurs de k ( car 2 clusters ), l'algorithme calcul la fonction de coûts $Min(I_A) = \frac{1}{m} \sum_{i=1}^{m} \left\| x^{(i)} - \mu_{c^{(1)}} \right\|^2 = J(c^{(1)}, \dots, c^{(m)}, \mu_1, \dots, \mu_k)$ et sélectionne les deux valeurs d'initialisation qui minimisent donc l'inertie intra-classe pour $k = 2$
• si $k = 3$, le même processus ( 2 étapes précédentes ) est répété et les trois valeurs d'initiation qui minimisent le coût sont sélectionnées
pour chaque initiation aléatoire de 2 valeurs de k ( car 2 clusters ), l'algorithme calcul la fonction de coûts $Min(I_A) = \frac{1}{m} \sum_{i=1}^{m} \left\| x^{(i)} - \mu_{c^{(1)}} \right\|^2 = J(c^{(1)}, \dots, c^{(m)}, \mu_1, \dots, \mu_k)$ et sélectionne les deux valeurs d'initialisation qui minimisent donc l'inertie intra-classe pour $k = 2$
• le même processus est réalisé pour différents scénarios de k ( k > 1 et par exemple $<=20$ )
• pour chaque scénario des valeurs d'initiation de le nombre correspond à K sont identifiées et surtout un coût est connu car il minimise l'inertie intra-classe pour le k correspondant
• le choix de $k$ consistera à sélectionner parmi les coûts de chaque scénario de k ( $k = 2, K= 3, k = 4, ... , k = 20$), le scénario du coût dont la diminution est la dernière diminution de j en passant de k à k + 1

Si nous représentons graphique en ordonnée ( y ) les valeurs de la fonction coût et en abscisse ( x ) les valeurs de k, nous obtiendrons le graphique suivant :

astuce

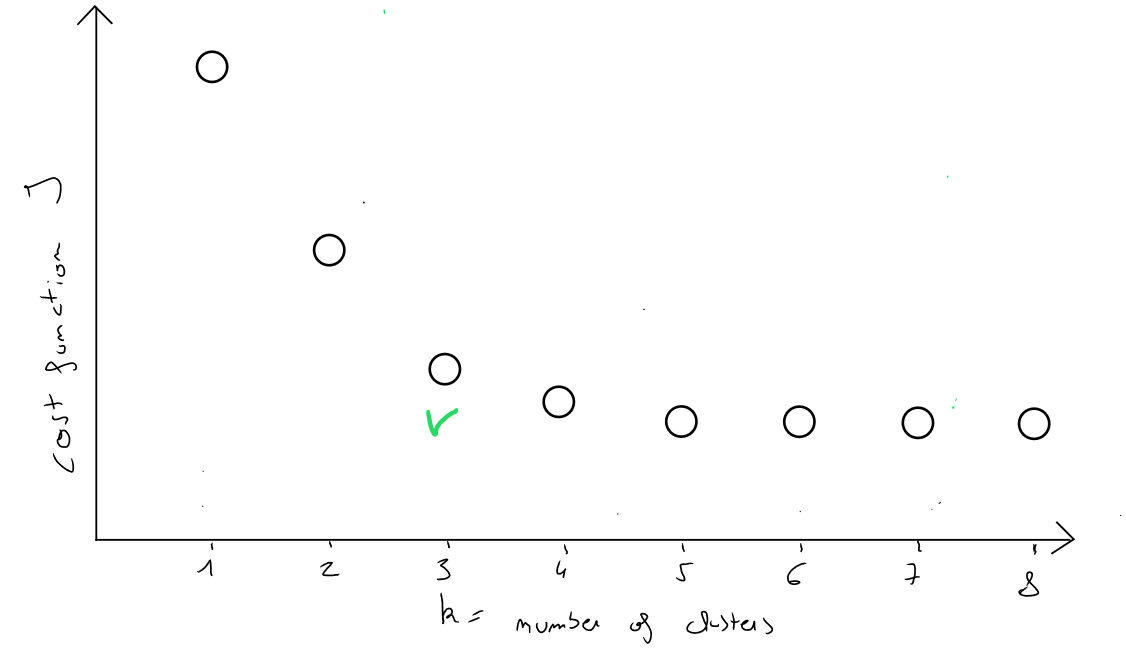
Si la dernière diminution de J la plus importante s’appliquer en passant de $k$ à $k +1$ classes, la partition en $k$ classes est bonne ! Prendre la plus petite valeurs de k serait incorrecte car si $k =$ nombre d'enregistrements, alors le coût serait de $0$.

Cette sélection de $k$ s'appelle la méthode elbow ( coude car la meilleure sélection de la fonction coût et donc de k correspond à la forme d'un coude)

Classification ascendante hierarchique

La classification ascendante hiérarchique est une technique de la famille du clustering et se différencie par le fait qu'elle produit des suites de partitions emboîtées d’hétérogénéité croissantes, entre la partition en $k$ classes où chaque objet est isolé, et la partition en $k = 1$ classe qui regroupe tous les objets.

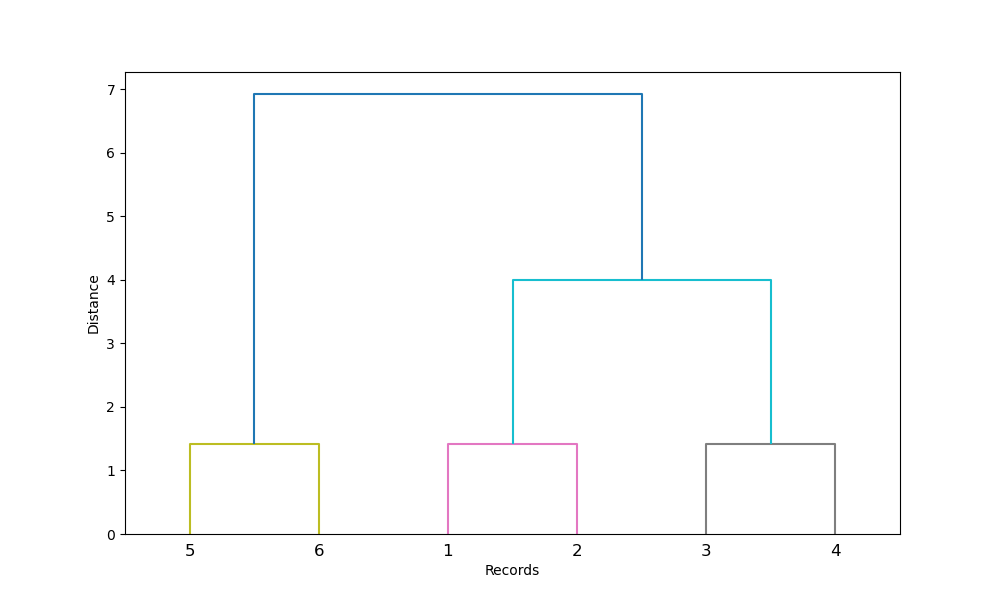
Cette méthode est également réalisée en plusieurs étapes.

• À l’étape 1 : l’algorithme définit par défaut chaque enregistrement comme étant un cluster individuel. Autrement dit, chaque individu est une classe. Si $n = 16$, nous démarrons avec 16 clusters comprenant chacun un enregistrement ;
• À l’étape 2 : les distances sont calculées entre les classes
• Lors du premier calcul de distance, lorsque $k = n$, c’est généralement la distance euclidienne qui est utilisée - ou Manhattan ou Minkowski
• Aux niveaux hierarchiques suivants ( lorsqu'une classe a plus d’un élément ), d'autres méthodes de calculs sont utilisées (reprises ci-après) ;
• À l’étape 3 : ( à un niveau hiérarchique supérieur ), les classes les plus proches sont fusionnées en une seule classe ;
• À l’étape 4 : l'algorithme réitère l’étape 2 jusqu’à l'obtention d'une classe unique qui contient tous les enregistrements ;

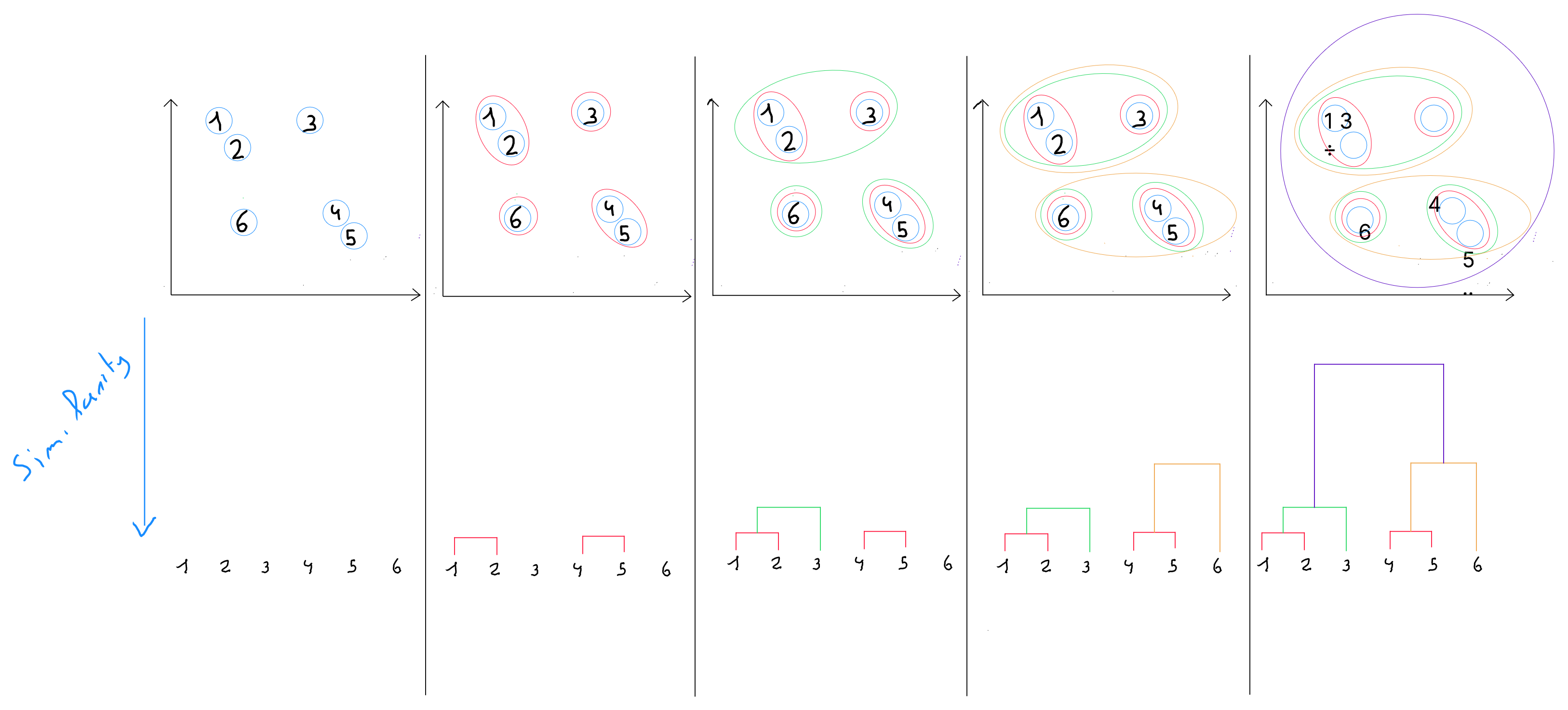
dendrogramme

La suite des partitions est représentée par un arbre appelé dendrogramme. Cet arbre peut être coupé à une hauteur plus ou moins grande pour obtenir un nombre plus ou moins restreint de classes. Il permet de visualiser les répartition sachant qu'au plus on se retrouve à la base du dendrogramme, au plus la similarité est forte et par conséquence la proximité ( distance ).

Concrètement : on choisit à quelle hauteur on souhaite découper le dendrogramme pour sélectionner un certain nombre de classes. Ce choix peut être arbitraire selon le nombre de clusters souhaité mais il est recommandé de sélectionner la haut qui optimise la similarité intra-classe.

Distances inter-classes

L’algorithme de la classification ascendante hiérarchique fonctionne donc en recherchant à chaque étape les clusters les plus proches pour les fusionner, et le « sel » de l’algorithme réside dans la définition de la distance de deux classes ( clusters ) A et B.

On peut définir cette distance de multiple manière, chaque méthode ayant des avantages et inconvénients mais surtout s’applique également dans des conditions très spécifiques ( formes des classes ).

attention

Rappel : à l’étape 1, c’est la distance euclidienne qui est utilisée pour regrouper les points les plus proches

Méthode du lien complet

La méthode du lien complet - ou complete linkage - retourne la distance maximale entre deux points enregistrements de deux clusters :

Distance maximale entre les deux points i et j tel que i appartient à R et J appartient à S

$$L(R, S) = \max(D(i, j)), \quad i \in R, \, j \in S$$

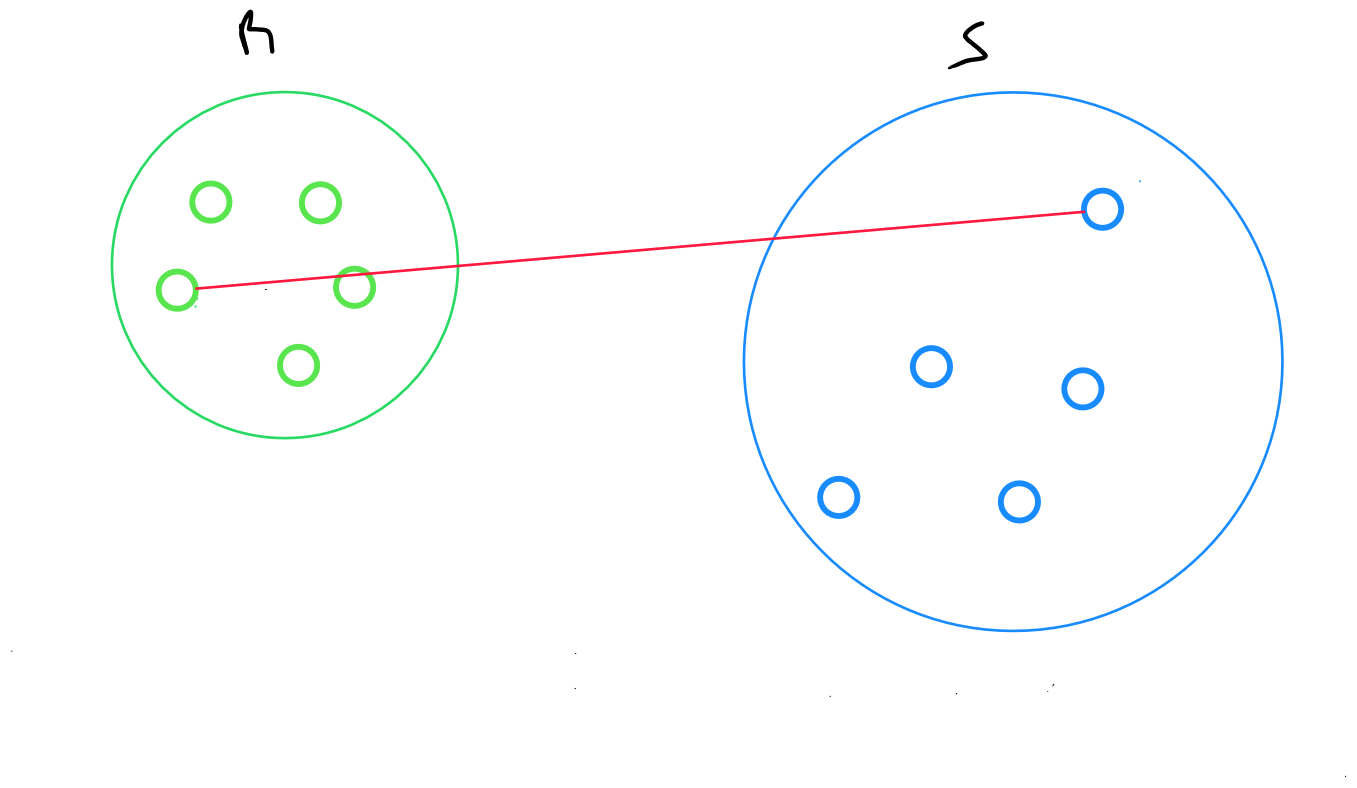
Par définition, cette mesure est très sensible aux valeurs aberrantes (« outliers ») et est de ce fait très peu utilisée

Méthode du lien simple

La méthode du lien simple ou single linkage retourne la distance minimale entre deux points enregistrements de deux clusters :

Distance minimale entre les deux points i et j tel que i appartient à R et J appartient à S

$$L(R, S) = \min(D(i, j)), \quad i \in R, \, j \in S$$

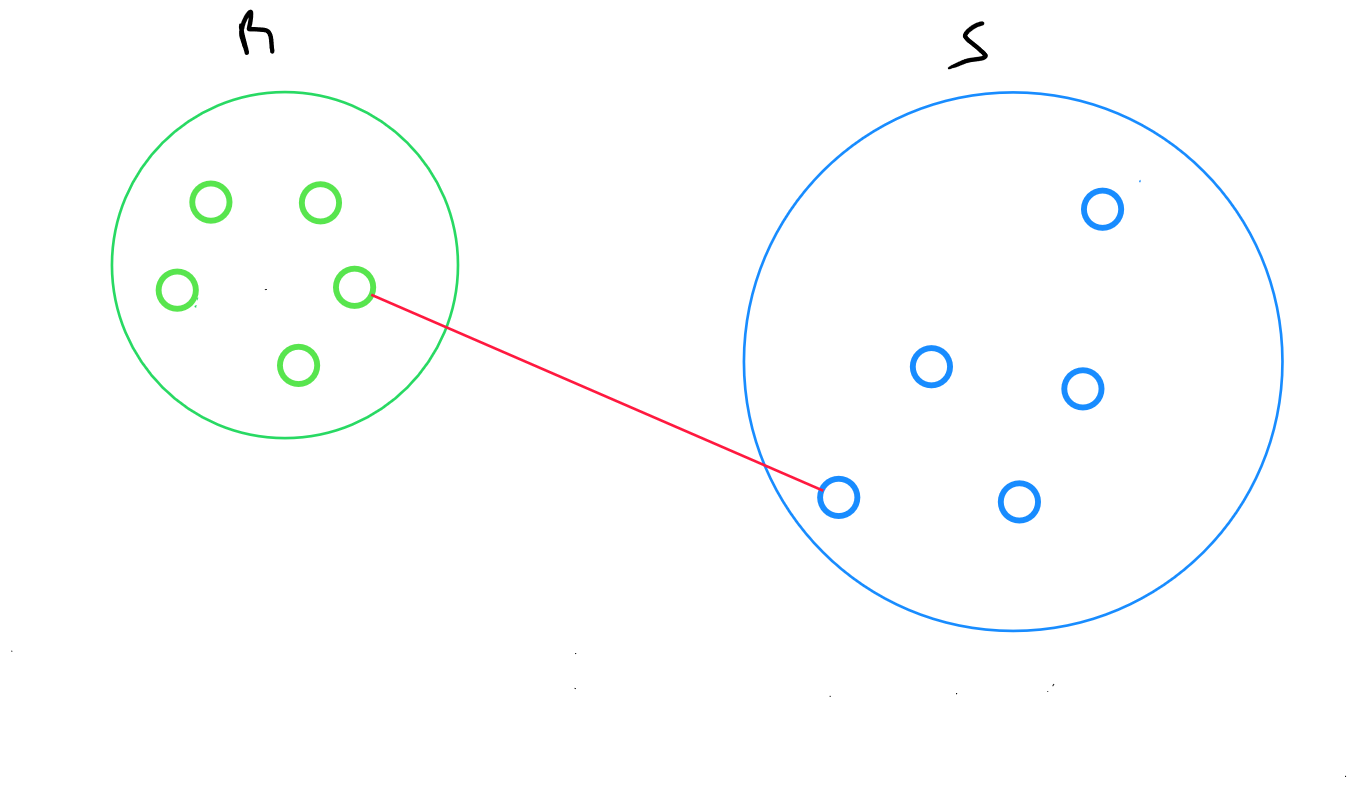
Le point faible de cette méthode est le fait qu’elle est sensible à « l’effet de chaine » : deux classes éloignées qui sont reliées par une chaine d’individus proches les uns des autres peuvent se retrouver regroupés.

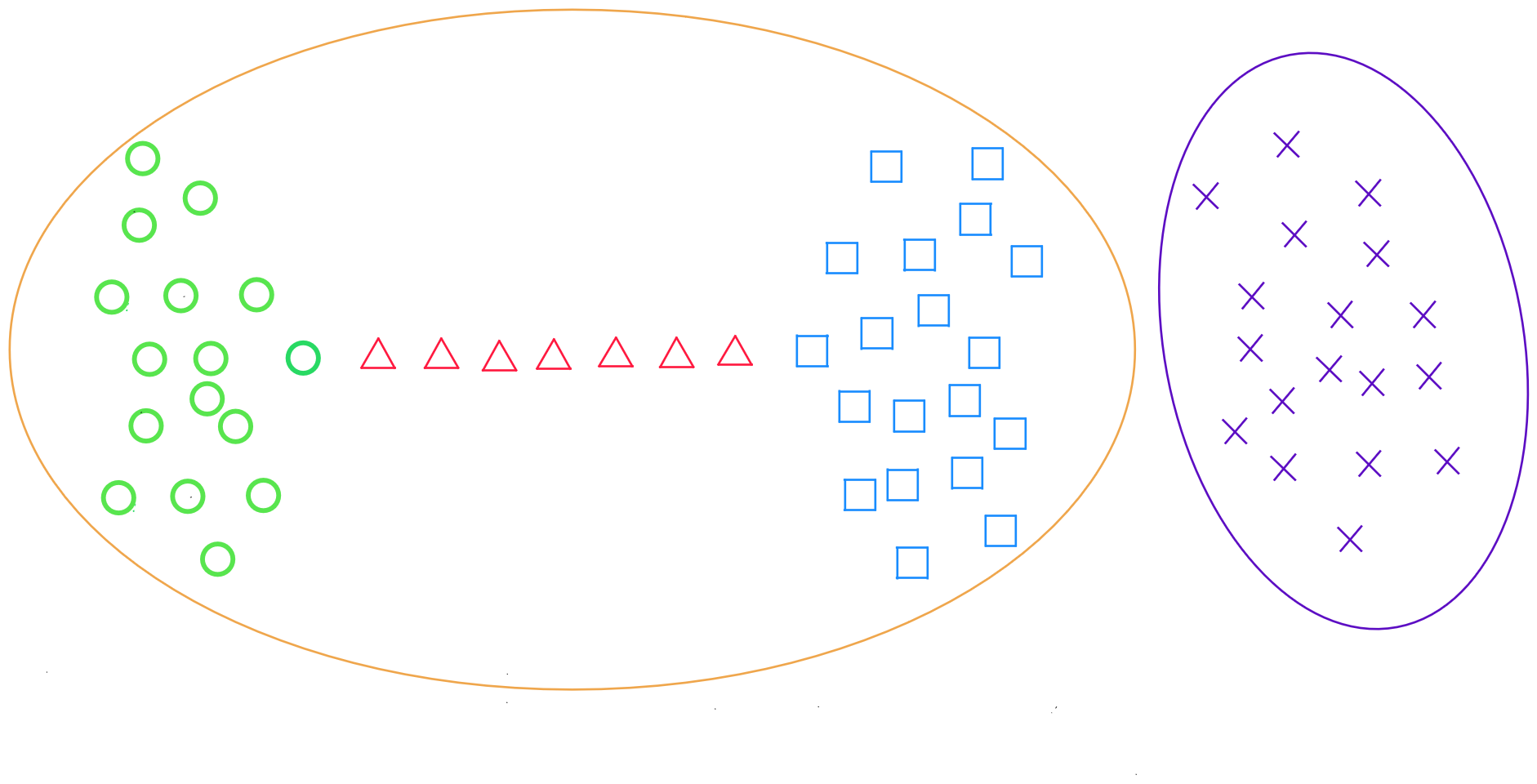
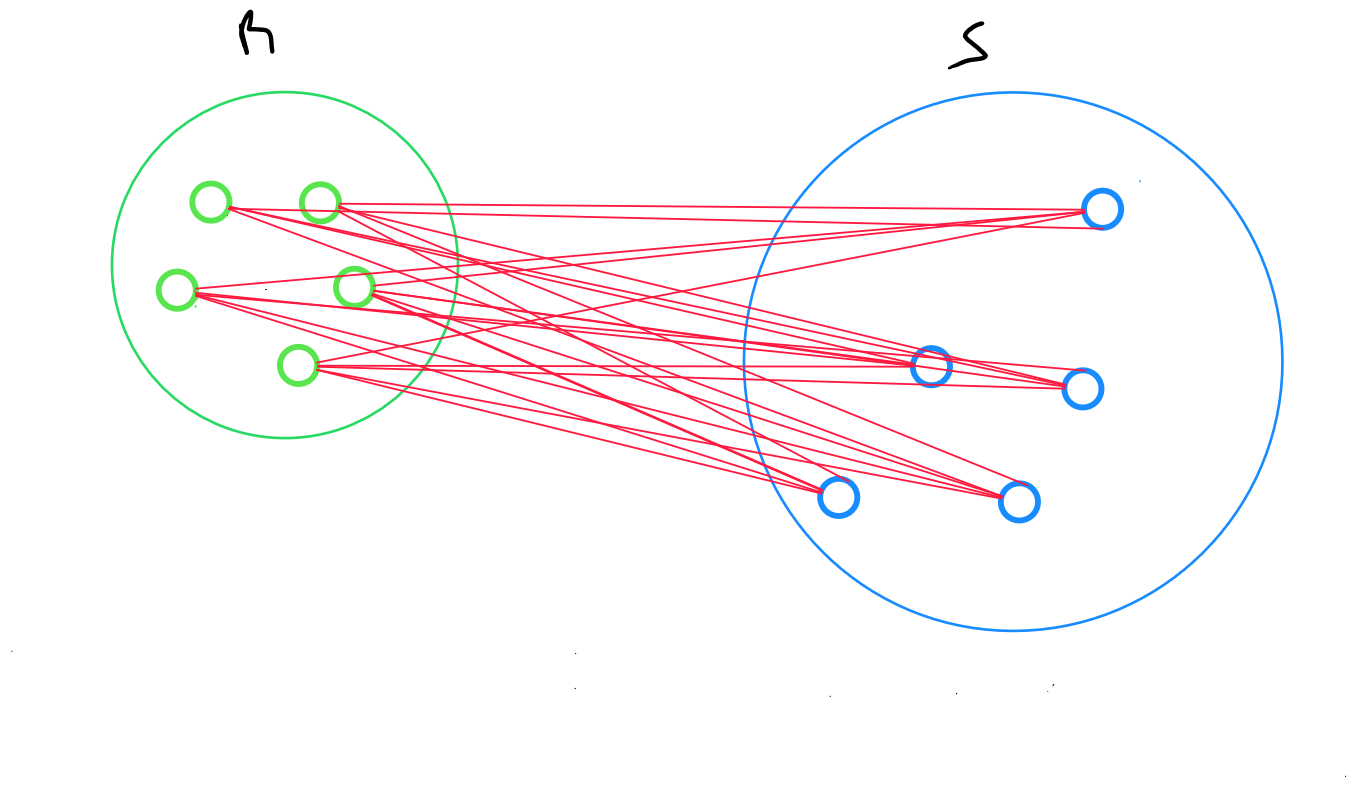
Méthode du lien moyen

La méthode du lien moyen - ou average linkage - retourne la distance moyenne entre tous les enregistrements de deux clusters :

Pour deux clusters R et S, on calcule la distance entre tous les enregistrements i dans R et tous les individus j dans S, puis on définit la moyenne arithmétique de ces distances

$$L(R, S) = \frac{1}{n_R + n_S} \sum_{i=1}^{n_R} \sum_{j=1}^{n_S} D(i, j), \quad i \in R, \, j \in S$$

où

$$n_R \text{ est le nombre de points dans } R \\$$$$n_S \text{ est le nombre de points dans } S$$

Méthode des centroïdes

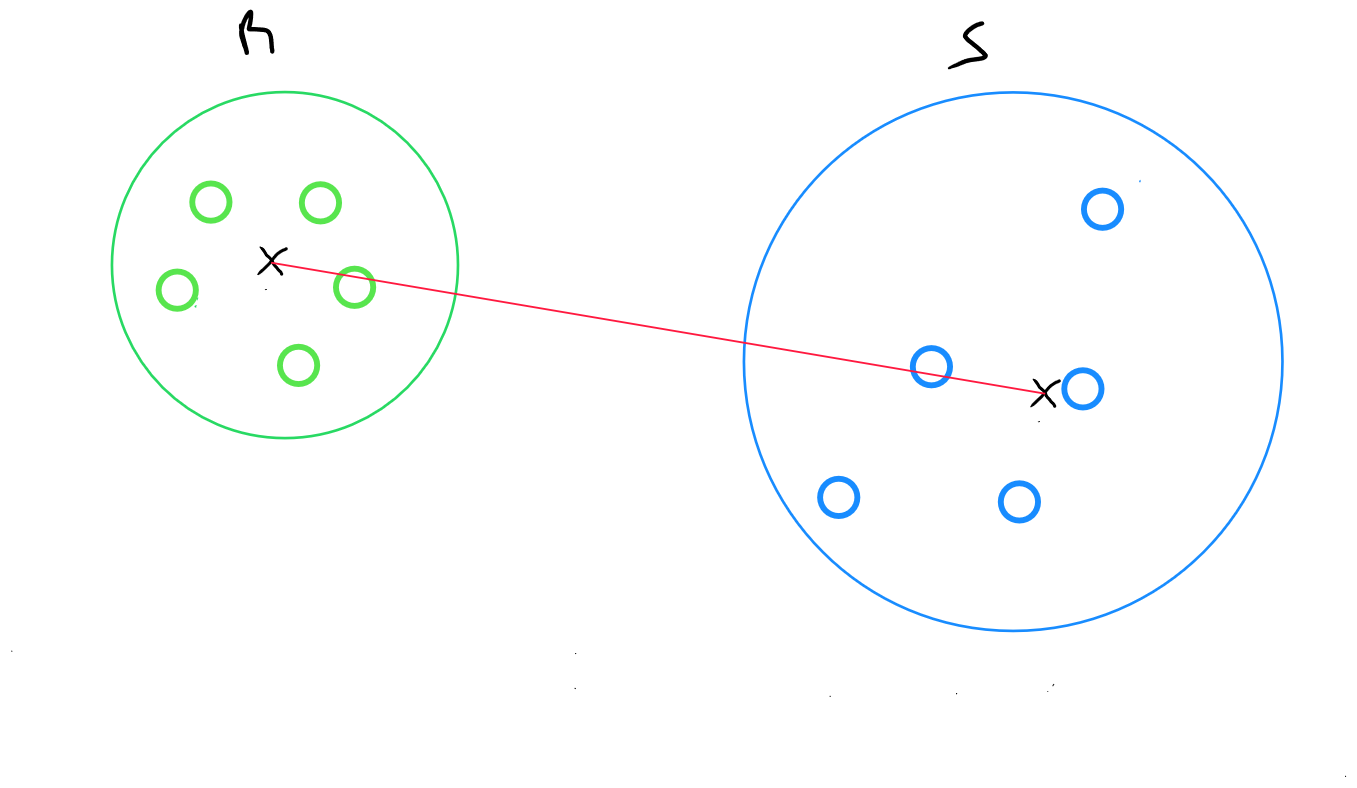
La méthode des centroïdes retourne la distance entre les centroïdes de deux clusters :

Pour deux clusters R et S, on calcule la distance entre le centroïde $u_i$ de R et le centroïde $u_j$ de S.

$$L(R, S) = \|\mathbf{c}_R - \mathbf{c}_S\|$$

où

$$\mathbf{c}_R = \frac{1}{n_R} \sum_{i \in R} \mathbf{x}_i$$

et

$$\mathbf{c}_S = \frac{1}{n_S} \sum_{j \in S} \mathbf{x}_j$$

Il s’agit de la méthode la plus simple à calculer, elle est plus robuste aux données aberrantes mais toutefois moins précise.

Méthode ward

Il s’agit de la méthode qui correspond le mieux à l’objectif de la classification ascendante hiérarchique, c’est-à-dire d’obtenir une inertie interclasse élevée.

Pour le passage d’une classification à k+1 classes à une classification en k classes ( regroupement de classes à un niveau hiérarchique supérieur ), on cherchera à fusionner les deux classes qui feront le moins baisser l’inertie interclasse. La distance entre deux classes est celle de leurs barycentres au carré, pondérée par les effectifs des deux clusters. La distance de Ward est sensible aux outliers mais est la plus utilisée.

$$D_{KL} = \frac{\|\mathbf{\bar{x}}_K - \mathbf{\bar{x}}_L\|^2}{\frac{1}{N_K} + \frac{1}{N_L}}$$

Code Python K-Means

import os
os.environ["OMP_NUM_THREADS"] = "2"

import numpy as np
import pandas as pd
from sklearn.datasets import make_blobs
from sklearn.preprocessing import MinMaxScaler
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

'''
##Synthetic dataset
n_samples = 500
n_features = 2
centers = 5
x, _ = make_blobs(n_samples=n_samples, n_features=n_features, centers=centers, random_state=42)
'''
dataset = pd.read_csv('data.csv')
x = data[['Column1', 'Column2', 'Column3','...']]



scaler = MinMaxScaler()
x_scaled = scaler.fit_transform(x)


inertia = []

K_range = range(1, 21)  
for k in K_range:
    kmeans = KMeans(n_clusters=k, n_init=100, random_state=42)  
    kmeans.fit(x_scaled)
    inertia.append(kmeans.inertia_)


plt.figure(figsize=(10, 6))
plt.plot(K_range, inertia, 'bo-')
plt.xticks(K_range) 
plt.xlabel('Number of Clusters (K)')
plt.ylabel('Inertia')
plt.title('Elbow Method for Optimal K')
plt.grid(True)
plt.show()

Sur base du graphique, nous identifions la valeur de k.

optimal_k = 4 #change based on elbow result
kmeans = KMeans(n_clusters=optimal_k, n_init=100, random_state=42)
kmeans.fit(x_scaled)

cluster_labels = kmeans.predict(X_scaled)

for i, label in enumerate(cluster_labels):
    print(f"Data point {i} is in cluster {label}")

Si nous utilisons que deux variables ( ou que le nombre de variables a été réduit à 2 suite à l'analyse en composantes principales ), il est possible de visualiser les clusters.

plt.figure(figsize=(10, 6))
plt.scatter(x_scaled[:, 0], x_scaled[:, 1], c=cluster_labels, cmap='viridis', marker='o', edgecolor='k', s=100)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='red', marker='X')  
plt.title(f'Clusters and Centroids (K={optimal_k})')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(True)
plt.show()


for i, label in enumerate(cluster_labels):
    print(f"Data point {i} is in cluster {label}")

Code Python CAH

import os
os.environ["OMP_NUM_THREADS"] = "2"

import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram, linkage
import matplotlib.pyplot as plt

'''
##Synthetic dataset
n_samples = 500
n_features = 2
centers = 5
x, _ = make_blobs(n_samples=n_samples, n_features=n_features, centers=centers, random_state=42)
'''
dataset = pd.read_csv('data.csv')
x = data[['Column1', 'Column2', 'Column3','...']]


scaler = MinMaxScaler()
x_scaled = scaler.fit_transform(x)

linked = linkage(x_scaled, method='ward')

plt.figure(figsize=(10, 7))
dendrogram(linked, orientation='top', distance_sort='descending', show_leaf_counts=True)
plt.title('Dendrogram using Ward’s Method')
plt.xlabel('Data points')
plt.ylabel('Distance')
plt.show()

# Number of clusters based on the dendrogram
optimal_k = 4  

hc = AgglomerativeClustering(n_clusters=optimal_k, metric='euclidean', linkage='ward')
cluster_labels = hc.fit_predict(x_scaled)

for i, label in enumerate(cluster_labels):
    print(f"Data point {i} is in cluster {label}")

Si nous utilisons que deux variables ( ou que le nombre de variables a été réduit à 2 suite à l'analyse en composantes principales ), il est possible de visualiser les clusters.

plt.figure(figsize=(10, 6))
plt.scatter(x_scaled[:, 0], x_scaled[:, 1], c=cluster_labels, cmap='viridis', marker='o', edgecolor='k', s=100)
plt.title(f'Clusters after Agglomerative Clustering (K={optimal_k})')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid(True)
plt.show()