Classifieur Naïf Bayésien
Le classifieur Bayésien est une technique supervisée de classement dont la particularité est qu'il préfère disposer de prédicteurs de type qualitatifs. Cela ne signifie pas pour autant que les variables quantitatives doivent être écartées mais ces dernières devront être transformées via le principe de discrétisation des variables continues.
Cette technique prédit des probabilités de classes et part de l'hypothèse que les variables sont conditionnellement indépendantes les unes des autres pour pouvoir définir la classe. Cette technique se base sur la probabilité individuelle ( de charque variable ) d'appartenance à une classe et multiplie ces probabilités individuelles ainsi que la probabilité générale de la classe.
Principe de Bayes
Le principe de Bayes s'intéresse à la probabilité conditionnelle qui consiste à relier la probabilité de A étant donné B à la probabilité de B étant donné A :
La probabilité de A étant donné B est la probabilité de B étant donné A multiplié par le rapport des probabilités de A et B
Par exemple :
- Quelle est la probabilité qu’un client qui utilise un iPhone ne renouvelle pas son abonnement ?
- Quelle est la probabilité qu’un client qui ne renouvelle pas son abonnement utilise un iPhone ?
Si A = arrêter son abonnement et B = utiliser un iPhone alors la probabilité d’arrêter son abonnement étant donné l’utilisation d’un iPhone est la probabilité d’avoir un iPhone étant donné un arrêt d’abonnement multiplié par la probabilité totale d’arrêter son abonnement, divisé par la probabilité totale d’avoir un iPhone
Probabilité conditionnelle individuelle
Le classifieur Naïf Bayésien suppose que les variables sont indépendantes. Une voiture peut être considérée comme une Ferrari si elle est rouge, sportive et dont la puissance max est de 780 Cv. Même si ces caractéristiques sont liées dans la réalité, l’algorithme déterminera que la voiture est une Ferrari en considérant indépendamment ses caractéristiques de couleur, type et de puissance et procédera comme suit :
- Quelle est la probabilité qu'une voiture rouge est une Ferrari ?
( probabilité conditionnelle individuelle ) - Quelle est la probabilité qu'une voiture sportive est une Ferrari ?
( probabilité conditionnelle individuelle ) - Quelle est la probabilité qu'un moteur de 780 cv est une Ferrari ?
( probabilité conditionnelle individuelle ) - Quelle est la probabilité d'une Ferrari sur toutes les voitures ?
( probabilité de classe )
L'algorithme multipliera ensuite ces probabilités individuelles qui seront divisées au dénominateur par les probabilités de toutes les classes afin d'obtenir une probabilité finale.
Formule
La formule de Bayes tente de répondre à la question suivante :
« Quelle est la probabilité qu’un enregistrement contenant un ensemble de valeurs prédictives , , …., appartienne une classe parmi l’ensemble des classes ? »
Cette formule peut être réécrite comme suit :
Le symbole représente le produit de toutes les classes.
Si nous décomposons cette formule, nous retrouvons les étapes suivantes :
- Estimer la probabilité conditionnelle individuelle pour chaque prédicteur d’appartenance aux classes - soit la probabilité que la valeur de l’enregistrement qui doit être classé appartienne à la classe , pour la première classe, pour la seconde classe, etc . Pour rappel, les caractéristiques sont évaluées de manière indépendantes
- Après évaluation indépendante, multiplier les probabilités conditionnelles individuelles d’appartenance à chacune des classes de chaque prédicteur soit la probabilité conditionnelle de la classe ,..., la probabilité conditionnelle de la classe
- Estimer la proportion d’enregistrements appartenant aux classes soit le total des enregistrements par rapport au total des enregistrements des autres classes. Le total des enregistrements ,..., rapport au total des enregistrements des autres classes ;
- Répéter les étapes 1,2 et 3 pour l’ensemble des classes (= probabilité conditionnelle de la classe … & proportion d’enregistrements appartenant à la classe )
- Appliquer la formule complète du classifieur naïf Bayésien pour l’ensemble des classes
- Assigner à l’enregistrement la classe correspondant à la probabilité la plus importante.
Décomposition des étapes
Prenons un exemple simplifié de l'utilisation du classifieur naïf Bayésien pour la détection de spam. Nous avons mis en place un modèle pour différencier les spams et emails. L’algorithme est entrainé ( il est capable de classer ) et reçoit l’email suivant :
« Cher John, serais-tu disponible pour un lunch entre amis demain ? Ne prends pas ton argent, c’est au tour de Lucas de régaler ».
Il identifie dans son set d’entrainement d’autres emails pour lesquels on retrouve les mots « Cher, Lunch, Amis, Argent » et pour lesquels il dispose déjà d’une étiquette – soit un classement mail ou spam .
Chaque mot est considéré comme une variable distincte et les enregistrements sont les emails :
= Cher (présence ou absence du mot "Cher")
= Amis (présence ou absence du mot "Amis")
= Lunch (présence ou absence du mot "Lunch")
= Argent (présence ou absence du mot "Argent")
Étape 1 : Estimer la probabilité conditionnelle individuelle pour chaque prédicteur d’appartenance aux classes .
Il s'agit de définir la probabilité d’appartenance individuelle à une classe sous-entend une probabilité conditionnelle individuelle c’est-à-dire la probabilité de l’évènement B étant donné que l’évènement A s’est produit. 𝑃 (𝐴│𝐵).
Dans notre cas, nous regarderons la probabilité d’appartenance à la classe et étant donné chaque prédicteur .
Total emails
𝑃 (𝐶ℎ𝑒𝑟│𝐸𝑚𝑎𝑖𝑙)
𝑃 (𝐴𝑚𝑖𝑠│𝐸𝑚𝑎𝑖𝑙)
𝑃 (𝐿𝑢𝑛𝑐ℎ│𝐸𝑚𝑎𝑖𝑙)
𝑃 (𝐴𝑟𝑔𝑒𝑛𝑡│𝐸𝑚𝑎𝑖𝑙)
Regardons maintenant la probabilité d’appartenance à la classe étant donné les valeurs du prédicteur soit .
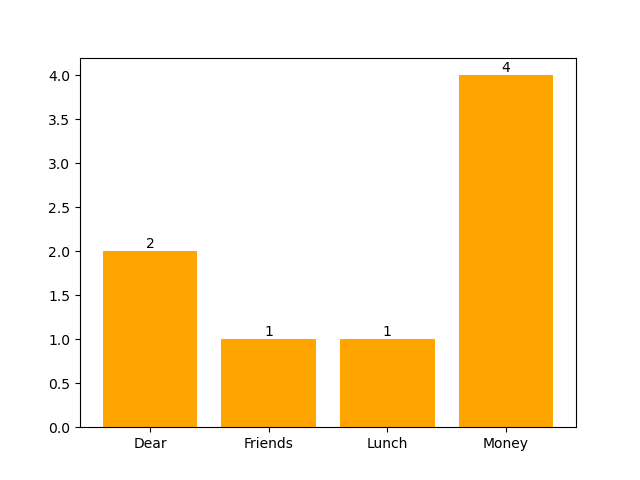
Total spams
𝑃 (𝐶ℎ𝑒𝑟│Spam)
𝑃 (𝐴𝑚𝑖𝑠│Spam)
𝑃 (𝐿𝑢𝑛𝑐ℎ│Spam)
𝑃 (𝐴𝑟𝑔𝑒𝑛𝑡│Spam)
Étape 2 : Estimation de la probabilité conditionnelle des classes.
Il s'agit de multiplier les probabilités conditionnelles individuelles d’appartenance des classes C_𝑖 de chaque prédicteur.
[ 𝑃 (𝐶ℎ𝑒𝑟 │𝐸𝑚𝑎𝑖𝑙) 𝑃 (𝐴𝑚𝑖𝑠 │𝐸𝑚𝑎𝑖𝑙) 𝑃 (𝐿𝑢𝑛𝑐ℎ │𝐸𝑚𝑎𝑖𝑙) 𝑃 (𝐴𝑟𝑔𝑒𝑛𝑡 │𝐸𝑚𝑎𝑖𝑙)]
[ 𝑃 (𝐶ℎ𝑒𝑟 │𝑆𝑝𝑎𝑚)𝑃 (𝐴𝑚𝑖𝑠 │𝑆𝑝𝑎𝑚)𝑃 (𝐿𝑢𝑛𝑐ℎ │𝑆𝑝𝑎𝑚) 𝑃 (𝐴𝑟𝑔𝑒𝑛𝑡 │𝑆𝑝𝑎𝑚)]
| Prédicteur | P(Prédicteur_Email) | P(Prédicteur_Spam) |
|---|---|---|
| Cher | 0.47 | 0.25 |
| Amis | 0.29 | 0.125 |
| Lunch | 0.18 | 0.375 |
| Argent | 0.06 | 0.50 |
| Produit | 0.47 x 0.29 x 0.18 x 0.06 | 0.25 x 0.125 x 0.375 x 0.50 |
Étape 3 : Estimation des proportion d’enregistrements appartenant aux classes
Nous devons encore tenir compte d’un élément important pour estimer la probabilité : il s’agit de la proportion de la valeur de la classe par rapport à l’ensemble des valeurs des deux classes. Soit : quelle est la proportion de spams par rapport à tous les emails reçus (spams & email). C’est une manière de s’assurer que la proportion sera mesurée à même échelle.
Sur emails, étaient des emails normaux et étaient des spams :
- Proportion d’emails normaux soit
- Proportion de spams soit
Étape 4 : répéter les étapes 1, 2 et 3 pour l’ensemble des classes. (Déjà réalisé dans notre exemple).
Étape 5 : appliquer la formule complète du classifieur naïf Bayésien pour l’ensemble des classes
Email:
Spams:
Étape 6 : assigner à l’enregistrement la classe correspondant à la probabilité la plus importante
Particularités de la technique
Il est important de noter que cette technique démontrera ses qualités à la condition sine qua non que les variables sont toutes indépendantes entre elle. Or, cette hypothèse est peu souvent applicable.
Toutefois, son avantage est qu'elle nécessite peu de données et que son procédé de calcul est relativement simple. Le classifieur naïf Bayésien est régulièrement utilisé pour le traitement du language naturel ( classification de texte, l'analyse de sentiment, ...).
Code Python Bayesian Classifier
# Step 1: Import necessary libraries
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report, confusion_matrix
# Step 2: Load the dataset with a filter on two categories
# These categories represent texts about baseball and space
categories = ['rec.sport.baseball', 'sci.space']
data = fetch_20newsgroups(subset='all', categories=categories, remove=('headers', 'footers', 'quotes'))
# Step 3: Explore the dataset
# Print the total number of documents, available categories, and an example document
print(f"Total number of documents: {len(data.data)}")
print(f"Categories: {data.target_names}")
print(f"Example document: {data.data[0]}")
# Step 4: Split the dataset into training and testing sets
# 70% of the data will be used for training, and 30% for testing
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.3, random_state=42)
# Step 5: Convert text data into a Bag of Words representation
# This creates a sparse matrix where each row corresponds to a document
# and each column corresponds to a word in the vocabulary
vectorizer = CountVectorizer()
X_train_counts = vectorizer.fit_transform(X_train)
# Step 6: Apply TF-IDF weighting to the Bag of Words matrix
"""
TF-IDF stands for Term Frequency-Inverse Document Frequency, a method used in Natural Language Processing (NLP)
to convert textual data into numerical vectors by assigning weights to words based on their importance.
1. Term Frequency (TF)
TF measures how frequently a word appears in a specific document. It is a local measure, specific to a single document.
TF (𝑡,𝑑) = (Number of occurrences of term 𝑡 in document 𝑑 ) / (Total number of terms in document 𝑑)
Words that appear more frequently in a document have a higher TF value.
Example: If the word "moon" appears 5 times in a document containing 100 words, then:
TF("moon")=5/100 =0.05
2. Inverse Document Frequency (IDF)
IDF measures the importance of a word across the entire corpus. It is a global measure, specific to all documents.
IDF(𝑡,𝐷) = log (N / (1+𝑛𝑡) )
N: Total number of documents in the corpus.
nt : Number of documents containing the term
Adding 1 in the denominator avoids division by zero if 𝑛𝑡 = 0
"""
# This adjusts the word frequencies based on their importance across all documents
tfidf_transformer = TfidfTransformer()
X_train_tfidf = tfidf_transformer.fit_transform(X_train_counts)
# Step 7: Train the Naive Bayes model
# Use the training data (TF-IDF matrix and corresponding labels)
model = MultinomialNB()
model.fit(X_train_tfidf, y_train)
# Step 8: Prepare the test data
# Transform the test set into the same format as the training set
X_test_counts = vectorizer.transform(X_test)
X_test_tfidf = tfidf_transformer.transform(X_test_counts)
# Step 9: Predict labels for the test data
y_pred = model.predict(X_test_tfidf)
# Step 10: Evaluate the model's performance
# Print the confusion matrix and classification report
cm_test = confusion_matrix(y_test, y_pred)
print(cm_test)
# Calculate overall accuracy
accuracy = cm_test.diagonal().sum() / cm_test.sum()
print(f"\nOverall Accuracy: {accuracy * 100:.2f}%")
# Step 11: Predict the class of a new message
# Example: A message that looks like spam
new_message = ["Bitcoin to the moons!!"]
# Transform the new message into a Bag of Words representation
new_message_counts = vectorizer.transform(new_message)
# Apply TF-IDF weighting to the new message
new_message_tfidf = tfidf_transformer.transform(new_message_counts)
# Step 12: Get the probabilities for each class
# This shows how likely the message is to belong to each category
proba = model.predict_proba(new_message_tfidf)
# Step 13: Predict the most likely class for the new message
prediction = model.predict(new_message_tfidf)
# Step 14: Display the results
print(f"\nMessage: {new_message[0]}")
print(f"Predicted Class: {data.target_names[prediction[0]]}")
# Display class probabilities in percentages
print("\nClass Probabilities:")
for i, category in enumerate(data.target_names):
print(f"Probability of '{category}': {proba[0][i] * 100:.2f}%")