Naive Bayes Classifier
The Naive Bayes classifier is a supervised classification technique that particularly favors qualitative predictors. This does not mean that quantitative variables should be excluded, but these should be transformed using the principle of discretization of continuous variables.
This technique predicts class probabilities and operates under the assumption that variables are conditionally independent from each other when defining the class. It relies on the individual probability ( of each variable ) belonging to a class and multiplies these individual probabilities by the overall class probability.
Bayes' Theorem
Bayes' Theorem focuses on conditional probability, linking the probability of A given B to the probability of B given A :
The probability of A given B is the probability of B given A multiplied by the ratio of the probabilities of A and B
For example :
- What is the probability that a customer who uses an iPhone will not renew their subscription ?
- What is the probability that a customer who does not renew their subscription uses an iPhone ?
If A = cancels subscription and B = uses an iPhone, then the probability of canceling the subscription given the use of an iPhone is the probability of having an iPhone given subscription cancellation multiplied by the total probability of canceling a subscription, divided by the total probability of using an iPhone.
Individual Conditional Probability
The Naive Bayes classifier assumes that the variables are independent. A car can be considered a Ferrari if it is red, sporty, and has a max power of hp. Even though these characteristics are related in reality, the algorithm will determine that the car is a Ferrari by independently considering its color, type, and power as follows :
- What is the probability that a red car is a Ferrari ?
(individual conditional probability) - What is the probability that a sports car is a Ferrari ?
(individual conditional probability) - What is the probability that a 780 hp engine is a Ferrari ?
(individual conditional probability) - What is the probability of a Ferrari among all cars ?
(class probability)
The algorithm will then multiply these individual probabilities, which will be divided by the probabilities of all classes to obtain a final probability.
Formula
The Bayes formula attempts to answer the following question :
« What is the probability that a record containing a set of predictive values , , …., belongs to a class among all classes ? »
This formula can be rewritten as :
The symbol represents the product over all classes.
Breaking down this formula, the steps are as follows :
- Estimate the individual conditional probability for each predictor belonging to classes – that is, the probability that the value of the record to be classified belongs to class for the first class, for the second class, and so on. Remember, the features are evaluated independently ;
- After independent evaluation, multiply the individual conditional probabilities of belonging to each class for each predictor, which is the conditional probability of class , ..., and the conditional probability of class ;
- Estimate the proportion of records belonging to classes , i.e., the total records of relative to the total records of other classes. Similarly for classes relative to the total records of other classes ;
- Repeat steps 1, 2, and 3 for all classes (= conditional probability of class ... & proportion of records belonging to class ) ;
- Apply the complete Naive Bayes classifier formula for all classes ;
- Assign the record to the class with the highest probability ;
Step Breakdown
Let’s take a simplified example of using the Naive Bayes classifier to detect spam. We have set up a model to differentiate between spam and regular emails. The algorithm is trained ( it can classify ) and receives the following email :
« Dear John, would you be available for lunch with friends tomorrow ? Don’t bring any money, it’s Lucas’s turn to treat ».
It identifies other emails in its training set that contain the words « Dear, Lunch, Friends, Money » for which it already has a label -either mail or spam -.
Each word is considered a distinct variable, and the records are the emails :
= Dear (presence or absence of the word "Dear") ;
= Friends (presence or absence of the word "Friends") ;
= Lunch (presence or absence of the word "Lunch") ;
= Money (presence or absence of the word "Money") ;
Step 1 : Estimate the individual conditional probability for each predictor belonging to classes .
This involves defining the individual probability of belonging to a class, which implies an individual conditional probability, i.e. the probability of event B given that event A has occurred: 𝑃 (𝐴│𝐵).
In our case, we look at the probability of belonging to class and given each predictor .
Total emails :
𝑃 (Dear│Email) ;
𝑃 (Friends│Email) ;
𝑃 (Lunch│Email) ;
𝑃 (Money│Email) ;
Now, let’s look at the probability of belonging to class given predictor , i.e., .
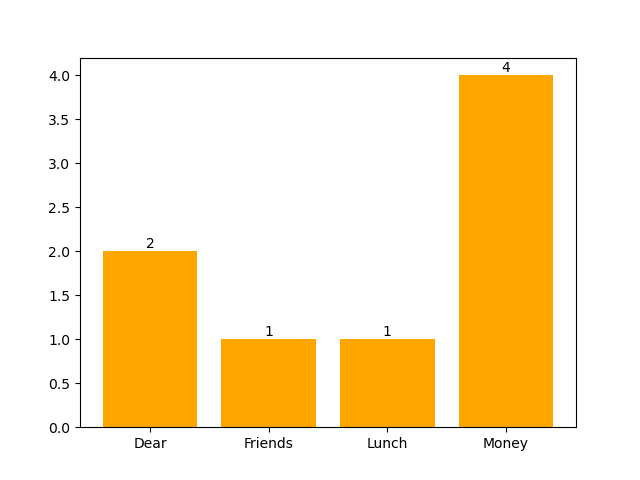
Total spam:
𝑃 (Dear│Spam)
𝑃 (Friends│Spam)
𝑃 (Lunch│Spam)
𝑃 (Money│Spam)
Step 2 : Estimate the class conditional probability.
This involves multiplying the individual conditional probabilities for each predictor belonging to classes .
[ 𝑃 (Dear │Email) 𝑃 (Friends │Email) 𝑃 (Lunch │Email) 𝑃 (Money │Email)]
[ 𝑃 (Dear │Spam) 𝑃 (Friends │Spam) 𝑃 (Lunch │Spam) 𝑃 (Money │Spam)]
| Predictor | P(Predictor_Email) | P(Predictor_Spam) |
|---|---|---|
| Dear | 0.47 | 0.25 |
| Friends | 0.29 | 0.125 |
| Lunch | 0.18 | 0.375 |
| Money | 0.06 | 0.50 |
| Product | 0.47 x 0.29 x 0.18 x 0.06 | 0.25 x 0.125 x 0.375 x 0.50 |
Step 3: Estimate the proportion of records belonging to classes
We must consider the proportion of the class value relative to all class values. In other words, what is the proportion of spams relative to all received emails (spam & email)? This ensures that the proportion is measured on the same scale.
Out of emails, were regular emails, and were spam :
- Proportion of regular emails or ;
- Proportion of spam or ;
Step 4 : Repeat steps 1, 2, and 3 for all classes. ( Already done in our example ).
Step 5 : Apply the complete Naive Bayes classifier formula for all classes
Email :
Spams :
Step 6 : Assign the record to the class with the highest probability
Technique Specifics
It is important to note that this technique works well only when variables are all independent of each other, which is rarely the case.
However, its advantage is that it requires little data, and its calculation process is relatively simple. The Naive Bayes classifier is often used for natural language processing (text classification, sentiment analysis, etc.).
Code Python Bayesian Classifier
# Step 1: Import necessary libraries
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report, confusion_matrix
# Step 2: Load the dataset with a filter on two categories
# These categories represent texts about baseball and space
categories = ['rec.sport.baseball', 'sci.space']
data = fetch_20newsgroups(subset='all', categories=categories, remove=('headers', 'footers', 'quotes'))
# Step 3: Explore the dataset
# Print the total number of documents, available categories, and an example document
print(f"Total number of documents: {len(data.data)}")
print(f"Categories: {data.target_names}")
print(f"Example document: {data.data[0]}")
# Step 4: Split the dataset into training and testing sets
# 70% of the data will be used for training, and 30% for testing
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.3, random_state=42)
# Step 5: Convert text data into a Bag of Words representation
# This creates a sparse matrix where each row corresponds to a document
# and each column corresponds to a word in the vocabulary
vectorizer = CountVectorizer()
X_train_counts = vectorizer.fit_transform(X_train)
# Step 6: Apply TF-IDF weighting to the Bag of Words matrix
"""
TF-IDF stands for Term Frequency-Inverse Document Frequency, a method used in Natural Language Processing (NLP)
to convert textual data into numerical vectors by assigning weights to words based on their importance.
1. Term Frequency (TF)
TF measures how frequently a word appears in a specific document. It is a local measure, specific to a single document.
TF (𝑡,𝑑) = (Number of occurrences of term 𝑡 in document 𝑑 ) / (Total number of terms in document 𝑑)
Words that appear more frequently in a document have a higher TF value.
Example: If the word "moon" appears 5 times in a document containing 100 words, then:
TF("moon")=5/100 =0.05
2. Inverse Document Frequency (IDF)
IDF measures the importance of a word across the entire corpus. It is a global measure, specific to all documents.
IDF(𝑡,𝐷) = log (N / (1+𝑛𝑡) )
N: Total number of documents in the corpus.
nt : Number of documents containing the term
Adding 1 in the denominator avoids division by zero if 𝑛𝑡 = 0
"""
# This adjusts the word frequencies based on their importance across all documents
tfidf_transformer = TfidfTransformer()
X_train_tfidf = tfidf_transformer.fit_transform(X_train_counts)
# Step 7: Train the Naive Bayes model
# Use the training data (TF-IDF matrix and corresponding labels)
model = MultinomialNB()
model.fit(X_train_tfidf, y_train)
# Step 8: Prepare the test data
# Transform the test set into the same format as the training set
X_test_counts = vectorizer.transform(X_test)
X_test_tfidf = tfidf_transformer.transform(X_test_counts)
# Step 9: Predict labels for the test data
y_pred = model.predict(X_test_tfidf)
# Step 10: Evaluate the model's performance
# Print the confusion matrix and classification report
cm_test = confusion_matrix(y_test, y_pred)
print(cm_test)
# Calculate overall accuracy
accuracy = cm_test.diagonal().sum() / cm_test.sum()
print(f"\nOverall Accuracy: {accuracy * 100:.2f}%")
# Step 11: Predict the class of a new message
# Example: A message that looks like spam
new_message = ["Bitcoin to the moons!!"]
# Transform the new message into a Bag of Words representation
new_message_counts = vectorizer.transform(new_message)
# Apply TF-IDF weighting to the new message
new_message_tfidf = tfidf_transformer.transform(new_message_counts)
# Step 12: Get the probabilities for each class
# This shows how likely the message is to belong to each category
proba = model.predict_proba(new_message_tfidf)
# Step 13: Predict the most likely class for the new message
prediction = model.predict(new_message_tfidf)
# Step 14: Display the results
print(f"\nMessage: {new_message[0]}")
print(f"Predicted Class: {data.target_names[prediction[0]]}")
# Display class probabilities in percentages
print("\nClass Probabilities:")
for i, category in enumerate(data.target_names):
print(f"Probability of '{category}': {proba[0][i] * 100:.2f}%")