Learning Concepts

In the previous chapter, we discussed learning in both supervised and unsupervised techniques.

However, the literature more frequently refers to supervised techniques when discussing learning principles. This makes sense, given that in the application of a supervised technique, we, as data scientists, play the role of the machine's teacher, training it and verifying whether the machine has learned properly, i.e. whether it performs its task correctly. Conversely, unsupervised techniques are not explicitly guided in learning, which is entirely autonomous for the machine. The goal is to highlight hidden trends or relationships that we, as data scientists, will interpret as either useful or not.

Furthermore, another fundamental distinction between supervised and unsupervised learning is that in supervised learning, the machine will autonomously continue the learning process afterward. We saw an example where, if we teach a machine that when an email contains the words « free », « lottery », and « money », there's a high probability it's spam ( undesirable mail ), the machine may later discover that the word « bitcoin » often appears with those words. Thus, without being explicitly programmed, it would integrate a new rule : identifying the word « bitcoin » as having a certain probability of being spam. In unsupervised learning, every time we apply the algorithm to new data, we obtain a new model, meaning the machine restarts the learning process from scratch.

Supervised Learning Process

To create a predictive model, we need data that includes the values we want to predict. These are referred to as « labeled data ». We also need columns considered as explanatory variables ( predictors, X : X₁, X₂, X₃,... ) and a variable to be explained ( the predicted variable Y ).

Splitting a DataFrame into Explanatory Variables and Target Variable

The first step in supervised learning is identifying and selecting the X variables and the Y column. Naturally, we assume that we have « clean » data, meaning that all analysis steps ( univariate statistical analysis ) and preparation ( especially transformations - feature engineering ) have been completed, and the data is structured in a tabular format. We also assume that the selection of the most useful predictors ( explanatory variables ) for building our model has already been completed.

We have a table containing X columns and a Y column, as follows :

X1	X2	X3	X...	Xn	Y
X1,1	X1,2	X1,3	...	X1,n	Y1
X2,1	X2,2	X2,3	...	Xn,n	Y2
...	...	...	...	...	...
Xn,1	Xn,2	Xn,3	...	Xn,n	Y3

tip

X_2,3 corresponds to the value of the 2nd row in the 3rd column

To convert our data into X and Y, we simply need to specify the columns belonging to X and the one belonging to Y. Writing [['Column Header 1', 'Column Header 2']] indicates multiple columns, whereas [] indicates a single column.

import pandas as pd

df = pd.DataFrame(data)


X = df[['X1', 'X2', 'X3']]  
y = df['Y']

Data Partitioning

The second step is to subdivide ( partition ) the records to use one partition for training the model ( teaching the machine ) and the other partition for validating the model ( checking whether the student, the machine, has learned properly ).

We partition the X and Y columns' records into two parts :

• Training set, which includes the learning data ;
• Test set, which includes the data used to verify the learning ;

The random partitioning of the data depends heavily on the amount of data available and the complexity of the techniques used. For example, if there is a limited amount of data, the partitioning might be : Training set $60$ ; Test set $40$.

However, if we have a large amount of data and the technique requires a significant number of records ( e.g., a neural network ), the partitioning might be : training set $80$ ; test set $20$.

💡 Tip: The partitioning between the "training" and "test" sets must be done randomly.

This partitioning can be easily achieved using the machine learning library scikit-learn :

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

X and y represent all our data. X contains multiple columns and numerous records. Y contains only one column but the same number of records as X. The train_test_split function will allow us to perform this partitioning, and it takes 4 arguments as described above. The first identifies X, the second identifies y, the third defines the test partition size ( in this case, $20$ ), and the fourth parameter, random_state, allows us to set a fixed starting point for the random process. This ensures that each time we run the train_test_split function with the same value for random_state (e.g., 42), we will get exactly the same data split.

Learning Step

In the learning phase, we apply a statistical technique to our training data. For example, in linear regression, a supervised parametric technique, the algorithm will go through several steps to determine the parameters, i.e. the effects of X values on Y values. For instance : the effect of a house’s square footage on its price.

The algorithm - comprising a series of steps ( including data partitioning ) - will provide us with a model that we can apply to new data.

Here is an example of learning by applying a predefined linear regression model ( We will break down this model in the chapter on linear regression ) :

model = LinearRegression()
model.fit(X_train, y_train)

Validation Step

Once we obtain a model, we will check, or validate, it. The simplest way to perform an initial validation is by verifying whether the model works correctly on the data it was trained on, but this time hiding the Y values and asking it to predict them. Since we are using the same data as in the learning phase, we expect to get an excellent score at this step, by comparing the predicted values with the real ones. The idea is to ensure the model is robust in its learning.

y_pred = model.predict(X_train)

We use the prediction function of our model on the same X values from which the model was created.

The prediction errors in the training set ( validation ) give us an indication of the model's fit ( underfitting or overfitting ).

warning

The error in the validation step, i.e. the difference between the predicted and actual values, should be minimal but should definitely not be 0. If you get 0, your model is overfitting. It knows the training data too well and will likely not generalize, resulting in a poor score on new data ( for example, during the test phase ).

Test Step

If the validation step is successful - i.e., we achieve high reliability ( small differences between the predicted and actual valuesn ) - we proceed to the test phase. If the validation step leads to low reliability, this means the model is undertrained.

**The test step consists of applying our model to the second partition of our data, which the model has not been trained on but where we know the values of both X and Y.**We apply the prediction function to X and compare the resulting Y values.

y_pred = model.predict(X_test)

We then check the difference between the predicted values and the actual values.

The result of the test phase should be slightly lower than in the validation phase, indicating that our model is able to define a generalizable rule. Based on the training data, it has been able to generalize the rule to any data.

Supervised Learning Evaluation

We need to use and evaluate multiple techniques to identify which will provide the most efficient model based on our data. Depending on the technique, we may also need to assess various configurations to achieve better or worse learning results.

The goal of supervised learning is to create a generalizable rule. This means achieving performance with new data. Two scenarios must be avoided : underfitting and overfitting. In underfitting, the machine fails the initial validation stage, meaning the model is poor with its training data and will also be poor with new data. In overfitting, the machine aces the validation stage ( perhaps too well ! ), but performs poorly when tested with new data, as it fits the training data too closely, rendering the model non-generalizable.

We detail these two cases below.

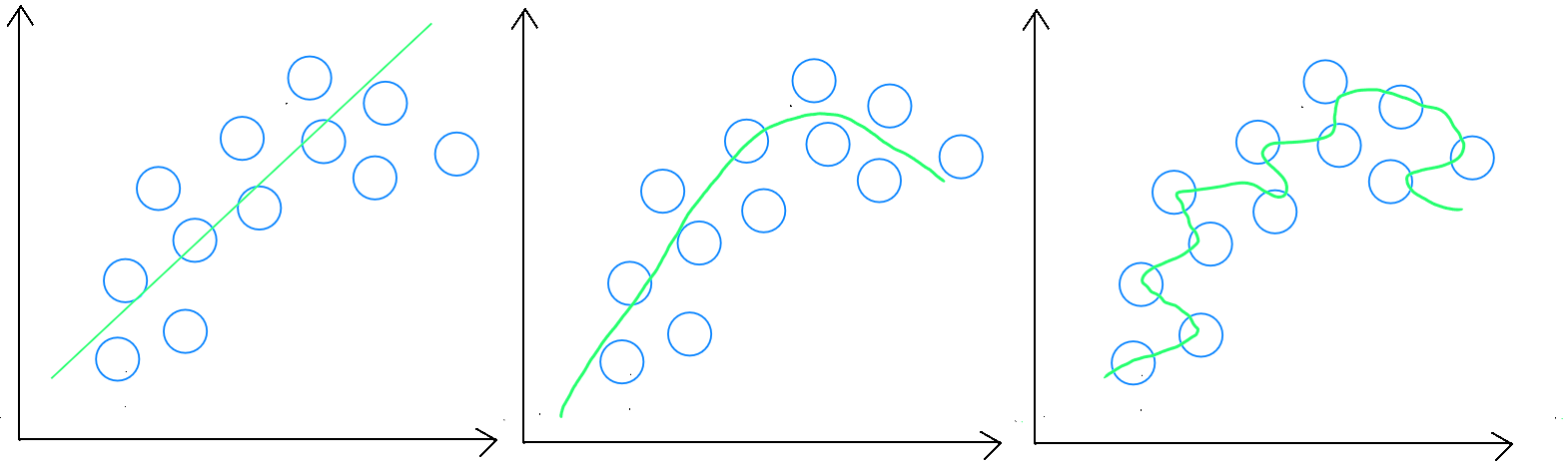
Estimation : underfitting, generalizable rule, and overfitting

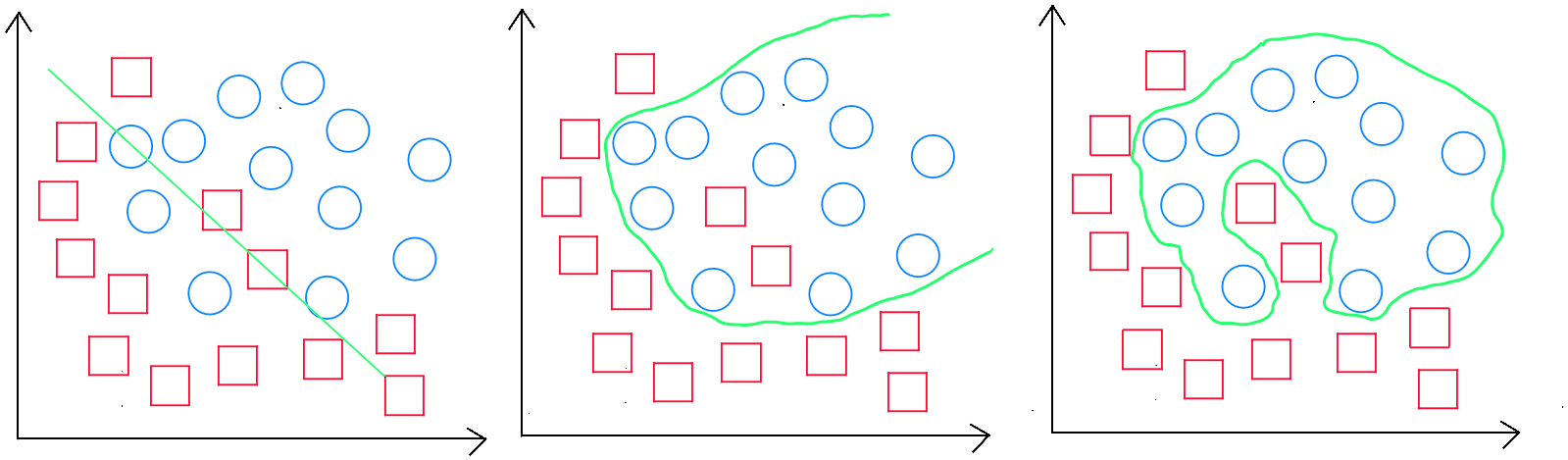
Classification: underfitting, generalizable rule, and overfitting

Generalizable Rule

Prediction errors in the training set ( validation ) provide an indication of the model's adjustment ( underfitting or overfitting ). For example, if the training error is 0, my model is certainly overfitting, as it is impossible to have a perfect model. Prediction errors in the validation set should be minimized since our model was trained based on this data. If the validation set shows a higher error rate, it is likely we are underfitting. Finally, prediction errors in the test set ( predictive errors ) measure the model's ability to generalize and should be slightly higher than in the validation set, but not too different, indicating that the model has created a generalizable rule.

Underfitting

Underfitting occurs when the training sample does not cover enough diverse cases, or the variables are insufficient in quantity, making it difficult for the model to generalize correctly. In absolute underfitting, we will obtain a poor result during the validation stage. However, we may also encounter a scenario where the training stage produces a seemingly « good » score, but applying the model to test data results in a poor score.

Overfitting

Overfitting occurs when the sample is too large. To adjust the model, either the sample size should be reduced, or the number of explanatory variables increased. In absolute overfitting, we get an excellent result during the validation stage, but a poor score when applying the model to test data.

Estimation Model Evaluation

In an estimation context, prediction errors in the training set ( validation ) indicate whether the model is underfitting or overfitting. For example, if the training error is 0, the model is likely overfitting. Errors in the validation set should be lower than in the test set since the model was trained based on the training set ( and thus the validation set ).

An error $(e)$ is the difference between the actual known value of $y$ and the predicted value, denoted as $\hat{y}$:

$e = y-ŷ$. We denote $e_i = (𝑦_i − ŷ_i )$ for a specific record's error.

warning

It is important to consider that different evaluation metrics are specific to the statistical technique used.

In most cases, the literature favors the use of Mean Square Error ( MSE ) or Root Mean Square Error ( RMSE ) for estimation evaluation :

$$MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$$

This formula can also be written as :

$$MSE = \frac{1}{n} \sum_{i=1}^{n} (e_i)^2$$

The MSE calculates the average squared differences and is thus more sensitive to large errors. RMSE, on the other hand, is computed as :

$$RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}$$

Or equivalently :

$$RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (e_i)^2}$$

where $e_i = y_i - \hat{y}_i$ ( the error for each record ), and $n$ is the total number of records.

The RMSE is expressed in the same units as the original data. For instance, if you are predicting house prices and obtain an RMSE of € 75,000, with the house price range being €350,000 - €500,000, the RMSE is not optimal. However, if the price range is €1,950,000 - €2,550,000, an RMSE of €75,000 is considered low and indicates a good model. The RMSE must be evaluated within the context of the data scale.

However, it is crucial to note that one of the foundational principles of a learning model is to normalize or standardize data, bringing it onto a common scale, which improves model efficiency. For instance, if we aim to create a model covering apartment sales, houses, and luxury villas, the model will contain numerous records, enhancing diversity and thus favoring a generalizable rule.

In this case, we want an RMSE value close to $0$, indicating a very good fit. Caution is necessary : an RMSE of $0$ during the validation phase ( applying the model to the same data it was trained on ) signals overfitting. Overfitting will be confirmed if the RMSE is much higher during the test phase. We aim for a low ( very low ) RMSE in validation, with a slightly less efficient RMSE in testing, but without a significant gap.

Classification Model Evaluation

In a classification context, our model will assign a class to the predicted value. For example, in a two-class classification model ( e.g. contagious (1) / non-contagious (0) ), $\hat{y}$ will have a final possible value of $1$ or $0$. Of course, we will not obtain a perfect model. Consequently, for some values of $y = 1$, our $\hat{y}$ will sometimes be $1$ and sometimes $0$.

If we have more than two classes, such as Good, Average, or Bad, $\hat{y}$ will have final possible values of $1$, $2$, or $3$, and for some values of $y = 1$, our $\hat{y}$ will sometimes be $1$, $2$, or $3$.

To evaluate a classification model, we create a matrix - the confusion matrix - which summarizes correct and incorrect classifications. This matrix allows us to calculate the precision rate and/or the overall error rate.

For example, in a model where the goal is to predict whether $\hat{y}$ is $1$ or $0$, the matrix will contain 4 cells as follows :

	Y = 0	Y = 1
ŷ = 0	55	3
ŷ = 1	9	33

To calculate the precision rate, we sum the correct classifications and divide by the total :

$$\text{Precision Rate} = \frac{\color{green}{55} + \color{green}{33}}{\color{green}{55} + \color{red}{3} + \color{red}{9} + \color{green}{33}} = \text{88\%}$$

To calculate the overall error rate, we subtract the precision rate from $1 = 22\%$:

$$\text{Overall Error Rate} = 1 - \text{Precision Rate}$$

What interests us are the correct predictions : true negatives ( non-contagious correctly predicted as non-contagious ) and true positives ( contagious predicted as contagious ) compared to false positives ( non-contagious predicted as contagious ) and false negatives ( contagious predicted as non-contagious ). The matrix looks like this :

	Y = 0 Non-Contagious	Y = 1 Contagious
ŷ = 0	True Negatives	False Negatives
ŷ = 1	False Positives	True Positives

In our case, we defined a threshold of $0.5$, meaning a result $>=0.5$ is considered contagious, while a result $<0.5$ is considered non-contagious. It is generally safer to have a model that predicts more people as contagious ( even if they are not ) rather than a model that predicts more contagious individuals as non-contagious. We are free, of course, to raise the threshold to, say, $0.65$ for more caution.

If our model aims to predict more than two classes, such as « Good », « Average », « Bad », we add $n$ additional columns to our matrix, where $n$ is the number of predicted classes.

	Y = 1 (Good)	Y = 2 (Average)	Y = 3 (Bad)
ŷ = 1 (Good)	True Positives "Good"	False Positives "Good" & False Negatives "Average"	False Positives "Good" & False Negatives "Bad"
ŷ = 2 (Average)	False Positives "Average" & False Negatives "Good"	True Positives "Average"	False Positives "Average" & False Negatives "Bad"
ŷ = 3 (Bad)	False Positives "Bad" & False Negatives "Good"	False Positives "Bad" & False Negatives "Average"	True Positives "Bad"

Once again, to calculate precision, simply sum all correct values and divide by the total number of records.