Régression linéaire

Le modèle de régression linéaire est l’un des modèles les plus populaires en machine learning pour réaliser une estimation ( prédire les valeurs d'une variable quantitative sur base de prédicteurs ). Il s'agit d'une technique paramétrique - le modèle doit trouver les meilleurs paramètres au regard des données -. Cette technique est utilisée pour ajuster la relation entre une variable numérique $Y$ ( variable dépendante ) et un ensemble de prédicteurs $x_1, x_2,...x_n$ - variables indépendantes.

Nous partons du postulat que $x$ et $y$ ne sont pas indépendants, c’est-à-dire que la connaissance de $x$ permet d’améliorer la connaissance de $y$. Il existe donc une corrélation entre $x$ et $y$ - pour rappel : au plus une variable $x$ est corrélée ( de manière positive ou négative ) à la variable $y$, au plus elle est importante pour notre modèle car on dit qu'elle est « discriminante ». - voir chapitre sur la ( corrélation ).

La régression linéaire n'accepte que des prédicteurs numériques, c'est à dire des variables quantitatives ou des variables qualitatives qui ont été transformées soit dans le cadre d'un encodage one-hot soit par le processus de numérisation de variables discrètes.

remarque

Certains schémas et concepts présentés ici sont inspirés du cours Machine Learning d'Andrew Ng, programme créé en collaboration entre Stanford university Online Education et DeepLearning.AI disponible sur Coursera. Retrouvez le cours original ici : Machine Learning by Andrew Ng.

Prédicteur unique

L’hypothèse est que la fonction suivante estime la relation entre les prédicteurs $x$ et la variable résultante $y$ :

$$\hat{Y} = b + w * x$$

 
Cette fonction correspond en réalité à l'équation d'une droite où $w$ correspond à la pente de la droite et $b$ est l'ordonnée à l'origine de la droite.

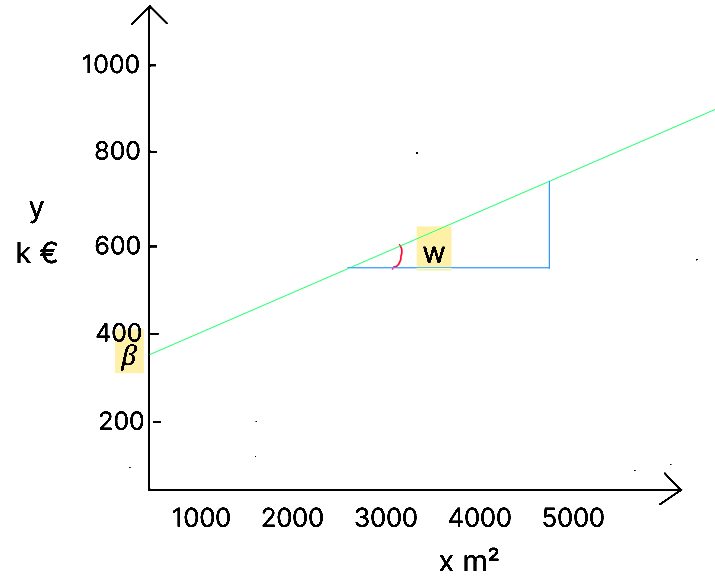
Les données permettent de comprendre la relation entre la variable dépendante et les variables indépendantes, c’est à dire d’estimer les coefficients et quantifier le bruit ϵ.

Prenons le cas des données suivantes reprenant la superficie d'une maison ( $x$ ) et le prix de vente ( $y$ ) :

$n$	Superficie m² $x$	Prix (k) $y$
1	2104	400
2	1416	232
3	1524	315
4	852	178
…	…	…
47	3210	870

 

L'objectif de l'algorithme est d'obtenir un modèle qui peut être représenté par la droite qui va minimiser les différences entre les valeurs réelles ( les bulles ) et les valeurs prédites ( la droite ). Sur base des valeurs de $x$, l'algorithme va définir $\hat{Y}$ ( qui n'est pas égal à $y$ ), en trouvant les valeurs de $b$ ( l'origine de la droite - si il n'y a pas de maison, il y a une valeur de base ( le terrain ) ) et de $w$ - la pente de la droite.

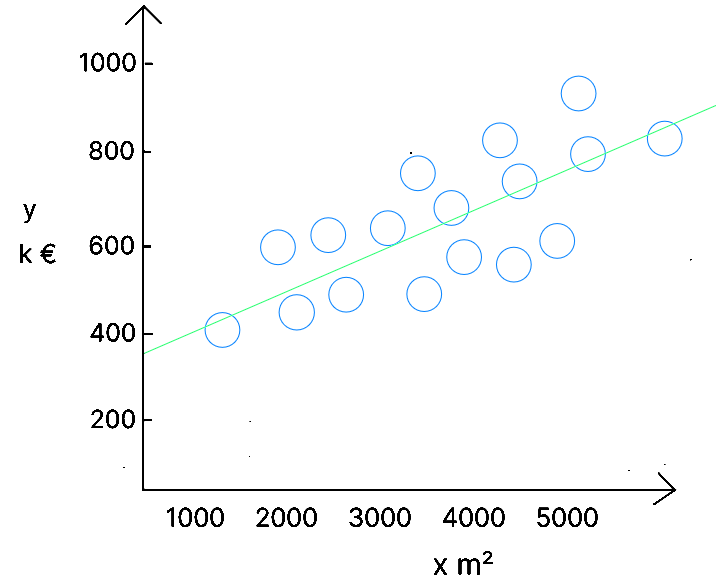
L'erreur ou le bruit

Comme nous l'avons abordé dans l'apprentissage supervisé, l'objectif d'un modèle de prédiction est de définir une règle généralisable. C'est à dire d'éviter d'obtenir un modèle qui est en sous-apprentissage ou sur-apprentissage. Une règle généralisable signifie que le modèle n'épouse pas parfaitement les données d'entrainement dans le but de pouvoir l'appliquer à de nouvelles données et obtenir un bon score.

Par conséquent, nous n'obtiendrons jamais un modèle réalisant des prédictions parfaites. Nous aurons toujours ce que nous appelons une erreur - notée $ϵ$ - ( une différence entre la valeur prédite $\hat{Y}$ et la valeur réelle $Y$ ) et notre objectif en tant que data scientist est de sélectionner le modèle - lors de l'évaluation - qui minimise cette erreur.

Pour une donnée $n_3$ nous connaissons $x$ qui correspond à $4500 m²$ et nous connaissons $y$ qui est égal à $705.000 €$. Après avoir implémenté notre algorithme sur nos données, un modèle a été créé , à savoir la droite $\hat{Y} = b + w * x$. Si nous regardons la valeur prédite pour $n_3$ - représentée par la ligne rouge ; c'est à dire le croisement entre notre droite représentant le modèle et le m² ; nous constatons que notre modèle nous donne un prix de $700.000 €$. Il y a donc une erreur de $5.000 €$ dans la prédiction. Cette erreur est logique car notre modèle a dû s'adapter à l'ensemble des données. C'est la raison pour laquelle il est important de comprendre que $\hat{Y} ≠ y$ mais $\hat{Y} = y + ϵ$ ( l'erreur ). Dans notre cas : $\hat{Y} = y + ( -5000 )$

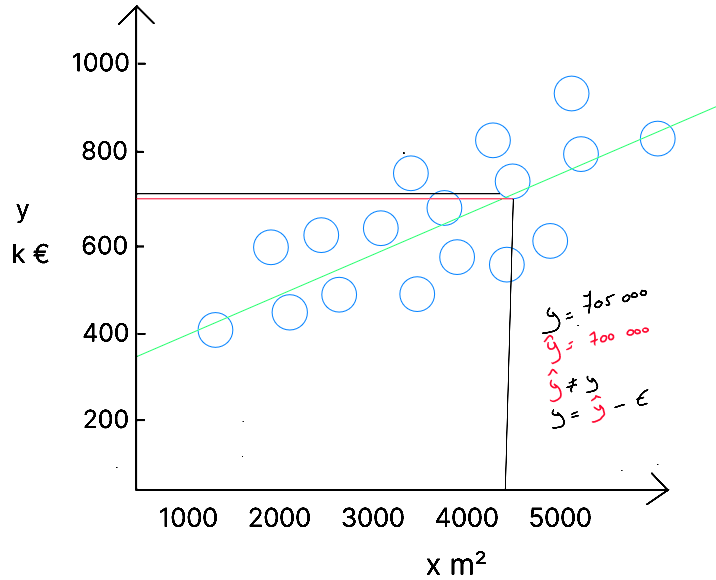
L'équation de la régression linéaire simple $y = \hat{Y}$ doit donc être réécrite comme suit :

$$y = b + w * x + ϵ$$

ou

$$\hat{y} = b + w * x$$

ou également :

$$\hat{y} = f_{w,b}(x)$$

Fonction prédiction en python régression simple

def predict(x, w, b):
    p = x * w + b
    return p

Fonction coût

Pour pouvoir réaliser un apprentissage, nous avons réparti au préalable nos données en variables explicatives ( $x$ ) et variable cible ( $y$ ) et, lorsque nous réalisons un modèle de régression linéaire, nous disposons de valeurs pour les $x$ et les $y$ correspondant. L'objectif de notre modèle $\hat{Y} = b + w * x$ est donc de définir $w$ et $b$.

Comment notre algorithme va-t-il procéder pour trouver les valeurs de $w$ et $b$ ? Rien de plus simple ! Comme nous l'avons abordé précédemment, lors de l'étape d'apprentissage , la machine va considérer les valeurs des $x$ et des $y$ du set d'entrainement pour identifier $w$ et $b$ en fonctionnant de manière itérative sur base d'une fonction coût qu'il va minimiser.

Concrètement l'algorithme va utiliser la fonction $\hat{Y} = b + w * x$. Il va remplacer $x$ par les valeurs des données d'apprentissage et attribuer de manière aléatoire ( pour le démarrage ) une valeur à $b$ et une valeur à $w$. Il va ensuite calculer le poids des erreurs du modèle en ayant attribué ces valeurs initiales à $b$ et $w$, en analysant les différences entre les valeurs des $y$ et les valeurs des $\hat{Y}$ pour chaque enregistrement. Ensuite, pour pouvoir trouver l'optimal local - c'est à dire les valeurs de $w$ et $b$ qui minimisent le coût ( l'erreur ), il va utiliser un algorithme d'optimisation : le gradient descent.

La fonction coût à donc pour objectif de minimiser pour chaque enregistrement $\hat{y}-y$. Par convention, en machine learning, la fonction coût s'écrit $J$.

L'objectif de la fonction coût est donc de minimiser les erreurs, ce qui pourrait se noter comme suit : $J(w, b) = \min \sum_{i=1}^n (\hat{y}^{(i)} - y^{(i)})^2$` où l'erreur est portée au carré pour éviter qu'une erreur positive ne comble une erreur négatif.

Toutefois, cette formule n'est pas complète car nous souhaitons minimiser la moyenne des erreurs ; Pour cela, nous pouvons multiplier la somme des erreurs par $\frac{1}{m}$ soit $J(w, b) = \min \frac{1}{m} \sum_{i=1}^n (\hat{y}^{(i)} - y^{(i)})^2$ afin de normaliser la fonction coût par rapport au nombre d'enregistrements ;

Dans la littérature, nous retrouvons une adaptation de cette fonction afin de simplifier le calcul de la dérivé de la fonction coût. En effet, pour trouver l'optimal local, c'est à dire la fonction coût qui minimise les erreurs, nous utilisons l'algorithme du gradient descent qui va calculer la dérivée de cette fonction coût pour définir à chaque itération s'il doit augmenter ou diminuer $b$ et s'il doit diminuer ou augmenter $w$.

Le fonction coût s'écrit donc

$$J(w, b) = \min \frac{1}{2m} \sum_{i=1}^n (\hat{y}^{(i)} - y^{(i)})^2$$

et nous pourrions remplacer $\hat{y}$ par ($w \cdot x^{(i)} + b$) soit :

$$J(w, b) = \min \frac{1}{2m} \sum_{i=1}^n ((w \cdot x^{(i)} + b) - y^{(i)})^2$$

ou

$$J(w, b) = \min \frac{1}{2m} \sum_{i=1}^n (f(w,b)x^{(i)} - y^{(i)})^2$$

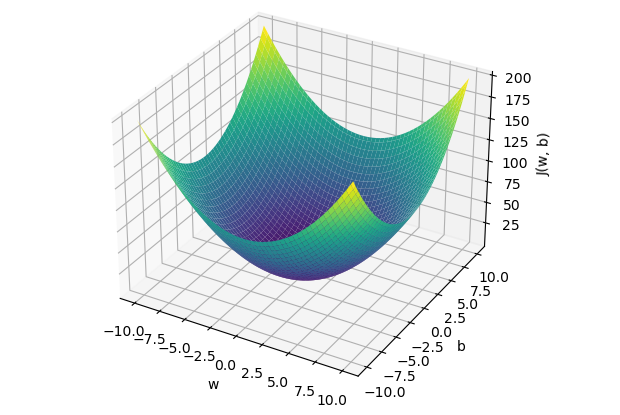
La fonction coût de la régression linéaire est de forme convexe, ce qui signifie qu'il existe un ensemble unique de valeurs pour $w$ et $b$ qui minimisent le coût. Visualisons trois exemples afin de démontrer cette forme convexe et l'optimal local. Pour l'exemple, nous retiendrons uniquement le coût pour $w$ soit $J(w)$ afin de pouvoir représenter cette fonction de coût dans un visuel en deux dimensions ( axe des ordonnées $y = J(w)$ et axe des abscisses $x =$ à la valeur de $w$ ). Nous allons tester trois valeurs de $w$, à savoir $w = 0 ; w = 0,5 ; w = 1$.

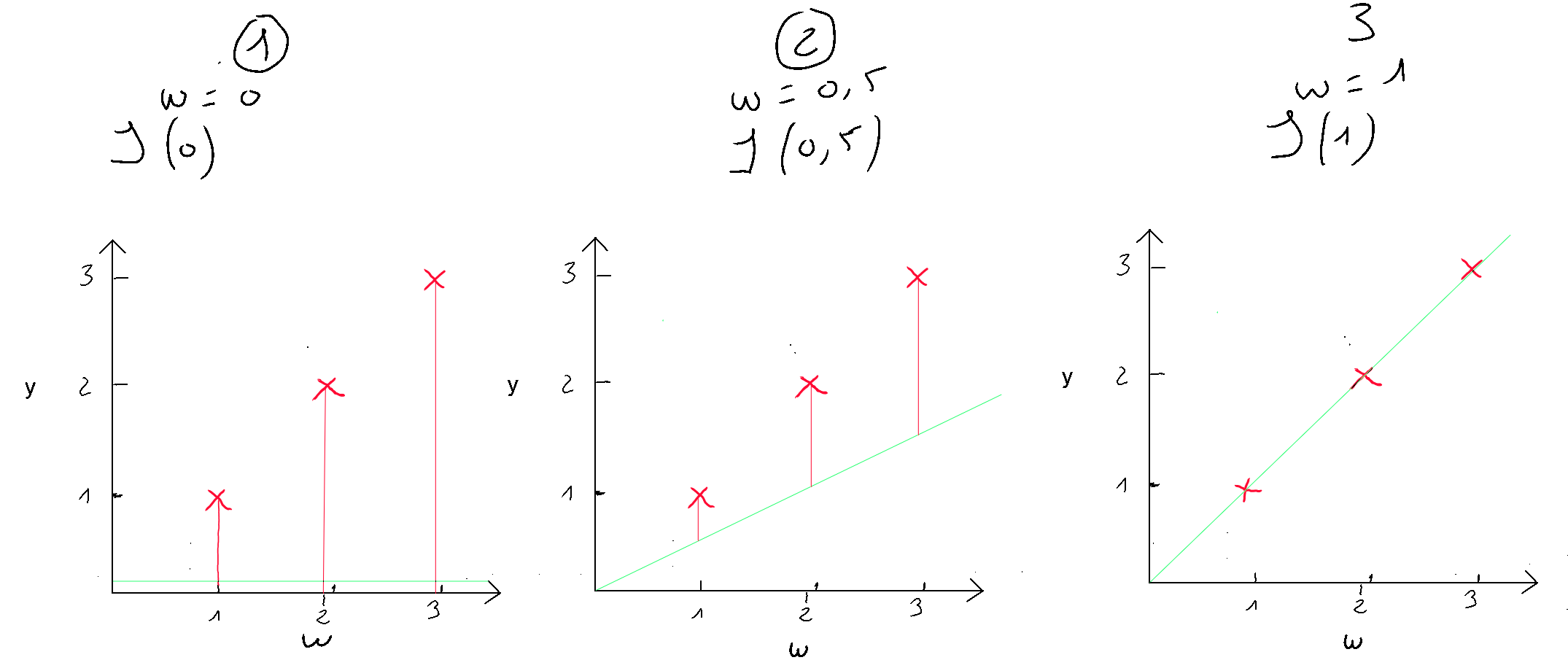
Si nous appliquons la formule de la fonction coût simplifiée à $w$, nous avons ceci $J(w) = \min \frac{1}{2m} \sum_{i=1}^n ((w \cdot x^{(i)}) - y^{(i)})^2$ ; que nous appliquons à nos cas :

1. (1) : $J(0) = \frac{1}{2m} \sum_{i=1}^n (1^2 + 2^2 + 3^2) = \frac{1}{6} (14) = 2.3$ ;
2. (2) : $J(0.5) = \frac{1}{2m} \sum_{i=1}^n ((0.5 - 1)^2 + (1 - 2)^2 + (1.5 - 3)^2) = \frac{1}{6} (3.5) = 0.58$ ;
3. (3) : $J(1) = \frac{1}{2m} \sum_{i=1}^n (wx^{(i)} - y^{(i)})^2 = \frac{1}{2m} \sum_{i=1}^n (0^2 + 0^2 + 0^2) = 0$ ;

Le cas numéro 3, nous montre que nous avons une erreur de 0. Lorsque $w = 1$, la prédiction est la meilleure. Disposons maintenant les résultats dans un visuel dans lequel nous représentons en axe des ordonnées $(y)$, le résultat de la fonction coût $j(w)$ et en abscisse ($x$), la valeur de $w$ initiée. Nous y retrouvons nos trois cas ( en rouge ) et si nous testions de nombreuses valeurs pour $w$, nous obtiendrons les autres cas ( en bleu ) pour découvrir au final, cette forme convexe qui finit toujours par un optimal local.

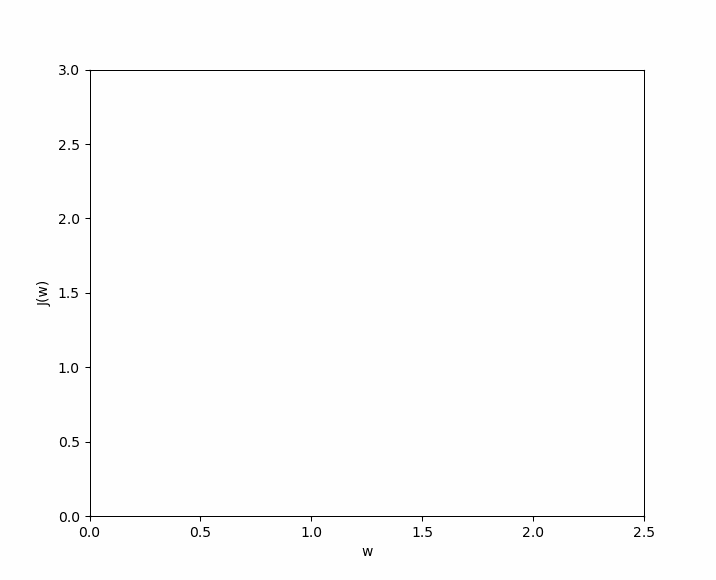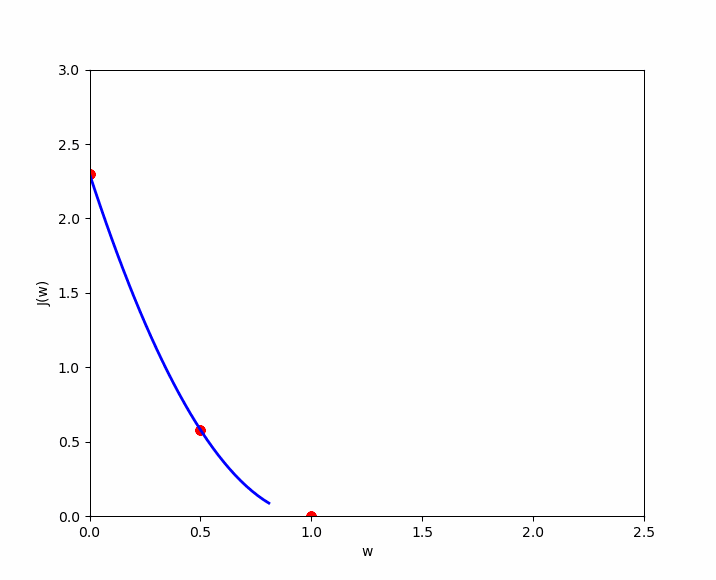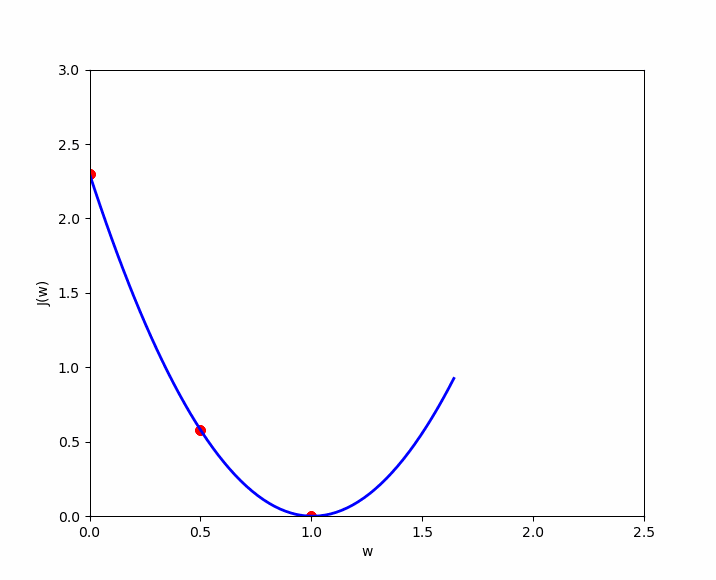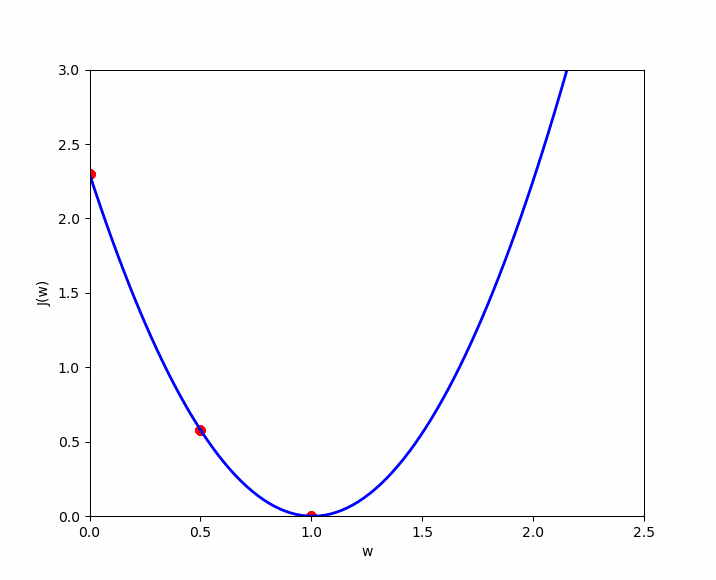
Fonction coût en python :

 def compute_cost(x, y, w, b):

    m = x.shape[0]
    cost = 0

    for i in range(m):
        f_wb = w * x[i] + b
        cost = cost + (f_wb - y[i])**2
    total_cost = 1 / (2 * m) * cost
          
    #regularization_cost = (lambda_ / (2 * m)) * np.sum(w**2)
    #total_cost += regularization_cost  
    return total_cost

Gradient descent

Le gradient descent est un algorithme d’optimisation qui permet de trouver un minimum local d’une fonction différentiable. Nous avons donc la fonction de coûts $J(w, b)$ et l'objectif de l'algorithme du gradient descent est de réduire ce coût par itération jusqu'à l'obtention de $min(J(w, b))$, l'optimal local.

Étapes

Le schéma de fonctionnement est relativement simple :

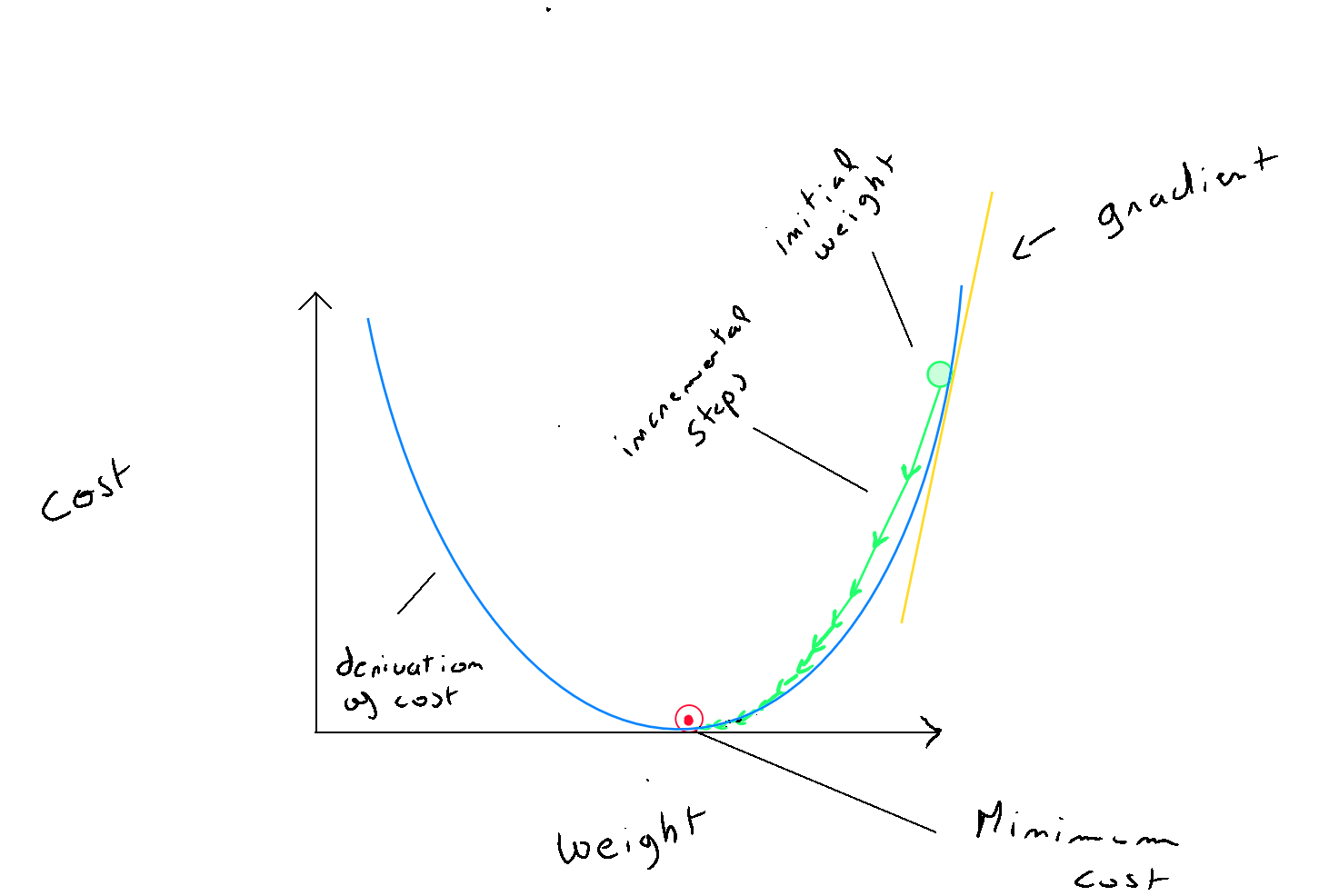
• Étape 1 : le gradient descent commence par appliquer la fonction coût : $J(w, b) = \frac{1}{2m} \sum_{i=1}^n ((w \cdot x^{(i)} + b) - y^{(i)})^2$ en définissant une valeur aléatoire pour $w$ et $b$. Sur base de ce calcul, l'algorithme va se retrouver à un certain endroit de la forme graphique de la fonction coût ( en forme de bol ) ;


• Étape 2 : pour pouvoir descendre dans le creux du graphique et atteindre l'optimal local ; A chaque itération, l'algorithme va calculer les dérivées de $w$ $\frac{d}{dw} j(w,b)$ et de $b$ $\frac{d}{db} j(w,b)$ qui permettent de définir la pente de la tangente au graphique de la fonction et qui va renseigner sur les mises à jours des paramètres. La pente va donc nous indiquer la direction à prendre pour rejoindre l'optimal local ( par exemple réduire $w$ = vers la gauche ; augmenter $w$ vers la droite ) ;


• Étape 3 : Bien que la direction soit indiquée, le data scientist va aider l'algorithme du gradient descent en définissant un taux d'apprentissage alpha noté $α$ qui correspond à la taille des « pas » de l'algorithme dans la direction identifiée pour rejoindre l'optimal local. Cette définition est très importante car si alpha est trop important, l'algorithme risque de rater l'optimal local et par conséquence, la fonction coût réaugmentera. D'autre part, si alpha $(α)$ est trop petit, l'algorithme atteindra l'optimal mais sera très lent ;


• Étape 4 : l'algorithme va itérer un certain nombre de fois jusqu'à ce que la fonction coût $J(w, b) = \frac{1}{2m} \sum_{i=1}^n ((w \cdot x^{(i)} + b) - y^{(i)})^2$ se réduit en deça d'un certain taux exemple =$<= 0,001$ ; cela signifie que l'optimal local a été trouvé.;

Pour l'implémentation du code, les valeurs de $w$ et $b$ doivent être remplacées à chaque itération, mais étant donné que les valeurs de l'itération précédente sont nécessaires dans le calcul des dérivés, il est important de définir, de manière temporaire la nouvelle valeur de w et la nouvelle valeur de b pour les remplacer par la suite :

astuce

Gradient descent

$J(w, b) = \frac{1}{2m} \sum_{i=1}^n ((w \cdot x^{(i)} + b) - y^{(i)})^2$

1. $temp_w = w - \alpha \frac{d}{dw} J(w, b) = w - \alpha \frac{1}{m} \sum_{i=1}^{m} [f_{w,b}(x^{(i)}) - y^{(i)}] x^{(i)}$ ;
2. $temp_b = b - \alpha \frac{d}{db} J(w, b) = b - \alpha \frac{1}{m} \sum_{i=1}^{m} [f_{w,b}(x^{(i)}) - y^{(i)}]$ ;
3. $w = temp_w$ ;
4. $b = temp_b$ ;

Choix des itérations et valeur alpha $(α)$

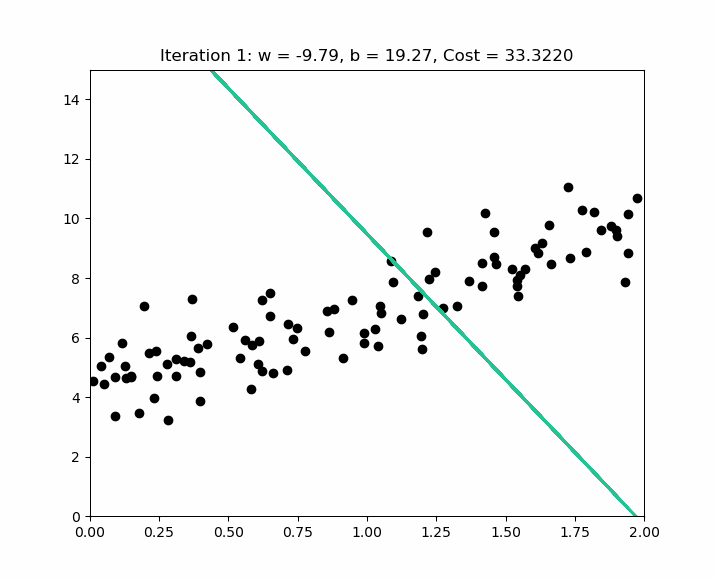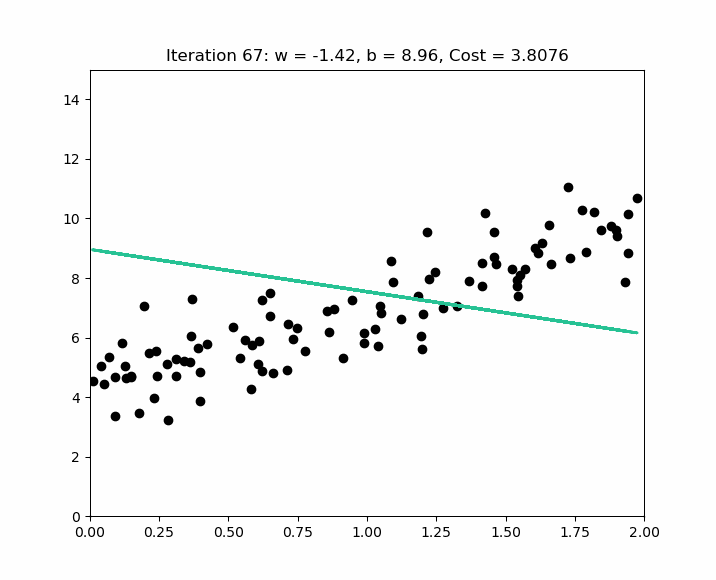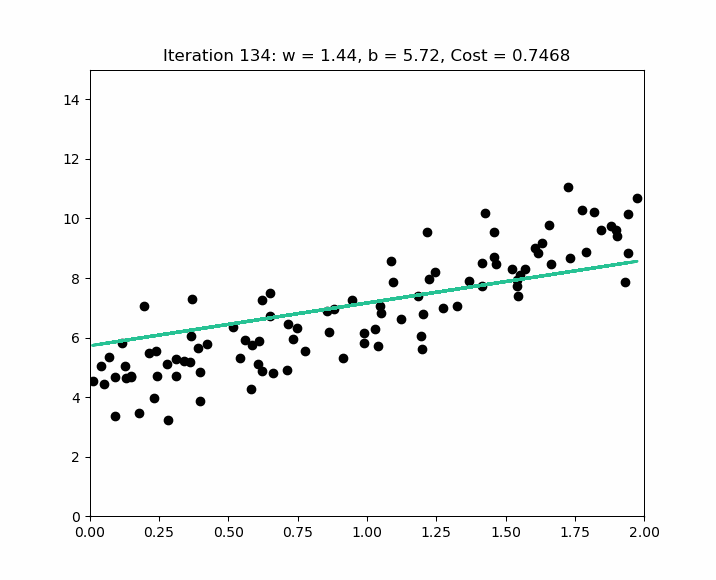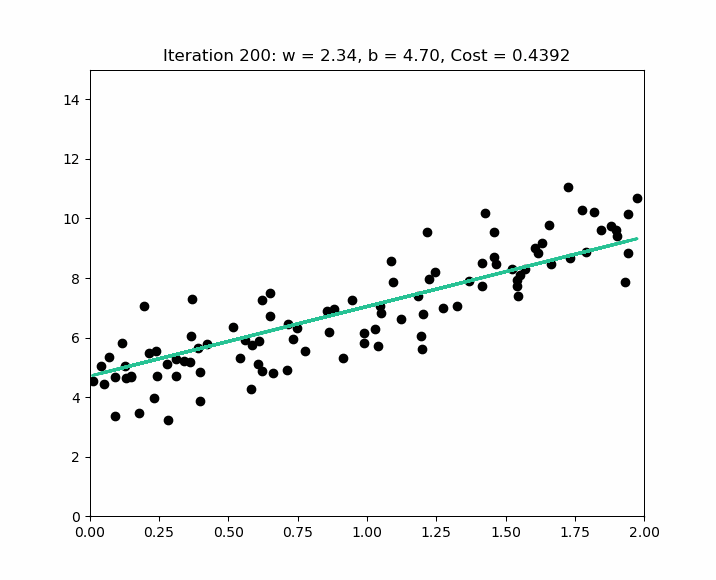
Un des points important est de définir correctement le nombre d'itérations ainsi que la valeur de alpha $(α)$ qui, complétée des valeurs des dérivés, va définir la grandeur des « pas » de l'algorithme vers l'optimal local. Bien entendu la définition de cette valeur va dépendre de nos données, et il est fondamental de ne pas choisir une valeur alpha trop faible ( graphique (1) ), car dans ce premier cas, l'apprentissage sera très lent ; ni de choisir une valeur de alpha trop élevée ( graphique (3) ), car dans ce second cas, le gradient descent va rater l'optimal local et la fonction coût va tout d'un coup réaugmenter. Le graphique (2) représente la situation idéale. Concernant le nombre d'itérations, il est recommandé d'intégrer une fonction « early Stop » de sorte que l'on peut définir un nombre d'itérations élevé, mais que si la fonction coût ne diffère pas d'une certaine réduction ( exemple $0,001$ ) entre deux itérations, l'optimal local est considéré. Il est important de noter que même si alpha $(α)$ est fixe ; c'est à l'aide de sa combinaison avec les dérivés que la direction et la grandeur des « pas » est déterminée et par conséquent, au fur et à mesure de l'arrivée près de l'optimal, ces diminutions seront de plus en plus réduites. Le choix de la valeur de lambda dépend de la valeur alpha. Par exemple si alpha est à $0,01$ alors lambda peut être initié à $1$ ou $10$ de sorte d'obtenir un chiffre légèrement inférieur à $1$ afin que la mise à jour de la valeur $w$ soit légèrement réduite.

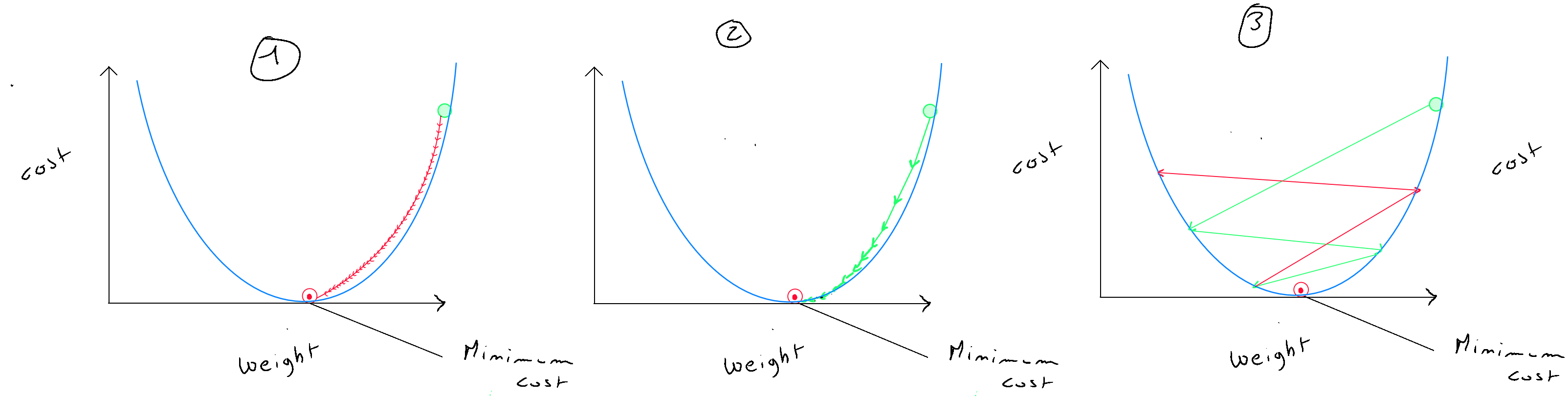
Comment choisir alpha $(α)$ ? L'idée est de commencer avec un alpha important ( exemple 0.3 ) ; si nous constatons que le coût réaugmente après une itération, c'est que alpha est trop important et le gradient descent rate l'optimal local. Dans ce cas nous essayons les valeurs de alpha comme suit : ( 0,1 ; 0,03 ; 0,01 ; 0,003 ; 0,001 ; etc. ). Voici un exemple d'itérations pour trouver l'optimal local sur des valeurs normalisées.

attention

Il est important de comprendre que le RMSE ( Root Mean Square Error ) - l'évaluation de la capacité prédictive du modèle - est sensible : (1) aux choix des variables ( dans le cas d'une régression linéaire simple, il vaut mieux avoir trouvé une variable très corrélée qui explique la variance de l'ensemble des données ) ; (2) au learning rate et (3) au nombre d'itérations (4) au principe de régularisation.

Iteration	Cost	dj_dw	dj_db	w	b
0	67.93	6.13	9.98	5.00	10.00
5000	3.39	1.28	2.23	0.35	2.24
10000	0.27	0.27	0.50	-0.62	0.50
15000	0.12	0.06	0.11	-0.82	0.12

Early stopping at iteration 17554 as cost change is less than 0.000001 ( w, b ) found by gradient descent: ( -0.85, 0.06 ).

Gradient descent en python :

def compute_gradient(x, y, w, b, lambda_):
    m = x.shape[0]
    dj_dw = 0
    dj_db = 0
    for i in range(m):
        f_wb = w * x[i] + b
        dj_dw_i = (f_wb - y[i]) * x[i]
        dj_db_i = f_wb - y[i]
        dj_db += dj_db_i
        dj_dw += dj_dw_i
    dj_dw = dj_dw / m
    dj_db = dj_db / m
    dj_dw += (lambda_ / m) * w
    return dj_dw, dj_db

Lancement du gradient descent:

def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function,lambda_):
    J_history = []
    p_history = []
    b = b_in
    w = w_in

    for i in range(num_iters):
        dj_dw, dj_db = gradient_function(x, y, w , b, lambda_)

       
        b = b - alpha * dj_db
        w = w - alpha * dj_dw

     
        if i<100000:      
            J_history.append( cost_function(x, y, w , b, lambda_))
            p_history.append([w,b])
            
        if i > 1 and abs(J_history[-1] - J_history[-2]) < 0.000001:
            print(f"Early stopping at iteration {i} as cost change is less than 0.000001")
            break 
            
    
        if i% math.ceil(num_iters/100) == 0:
            print(f"Iteration {i:4}: Cost {J_history[-1]} ",
                  f"dj_dw: {dj_dw}, dj_db: {dj_db}  ",
                  f"w: {w}, b:{b}")

    return w, b, J_history, p_history 

lambda_= 0.01
np.set_printoptions(precision=2)
w_init = 5
b_init = 10

iterations = 100000
tmp_alpha = 0.0003

w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha,
                                                    iterations, compute_cost, compute_gradient, lambda_)

print(f"(w,b) found by gradient descent: ({w_final},{b_final})")

Prédicteurs multiples

Nous avons abordé jusqu'à présent la régression linéaire de type simple, c'est à dire qu'une variable $x$ - prédicteur - sert à expliquer une variable $\hat{Y}$, variable prédite. La régression linéaire simple est utilisée dans le but de simplifier la compréhension du modèle de régression, et également par le fait qu'il est utile de pouvoir visualiser le processus en $2$ dimensions. Toutefois, dans la réalité, nous sommes amenés à utiliser un ensemble de colonnes considérézs comme variables explicatives ( prédicteurs ) pour une variable expliquée ( prédicte ) $\hat{Y}$.

La différence entre la régression linéaire simple et régression linéaire multiple réside donc dans le fait que la régression linéaire multiple utilise plusieurs $x$ : $x_1, x_2, x_3, ..., x_n$. Dans la régression linéaire simple, le gradient descent va fonctionner par itération pour trouver les valeurs de $w$ et $b$, la formule de la régression linéaire simple étant :

$$\hat{Y} = b + w * x$$

Dans une régression linéaire multiple, nous n'aurons pas une seule droite, mais autant que droites qu'il n'y a de colonnes $x$. Par conséquent, chaque $x$ aura un paramètre $w$ propre. Le seul élément qui ne change pas mais qui évidemment reste impacté par l'ensemble des colonnes, c'est la valeur de $b$ ; l'origine des droites.

$$\hat{Y} = b + w_1 x_1^{(i)} + w_2 x_2^{(i)} + w_3 x_3^{(i)} + ... + w_p x_p^{(i)}$$

Chaque enregistrement (i) - ligne - contiendra un ensemble de valeurs pour chaque colonne et par conséquent, chaque colonne aura un « poids » $w$.

Calcul vectoriel

En apprentissage automatique, on favorise dans le cas-là le calcul vectoriel car les opérations vectorielles sont parallélisées, c'est à dire que plusieurs calculs peuvent être effectués simultanément sur différents éléments du vecteur. De plus, les GPU ( Graphic process Unit ) sont très efficaces pour réaliser ces calculs en parallèle. Notons également que les vecteurs sont stockés dans la mémoire de manière contigu ( accès plus rapide aux données par le processeur ). D'un point de vue humain, la notation de l'opération vectorielle est simplifiée par des flèches au-dessus des $x$ $(\vec{x})$ et des $w$ $(\vec{w})$

La formule :

$$\hat{Y} = b + w_1 x_1^{(i)} + w_2 x_2^{(i)} + w_3 x_3^{(i)} + ... + w_p x_p^{(i)}$$

Peut donc être notée :

$$f_{\vec{w}, b}(\vec{x}) = \vec{w} \cdot \vec{x} + b$$$$\hat{Y} = b + \vec{w} \cdot \vec{x}$$

où
$\vec{x} = [x_1, x_2, x_3, ... , x_n]$ $\vec{w} = [w_1, w_2, w_3, ... , w_n]$

Code python régression linéaire multiple

def predict(x, w, b):
    p = np.dot(x, w) + b
    return p

Régression polynomiale

Nous avons abordé jusqu'à présent la régression linéaire. Or, il est important de considérer le fait que la distribution des données peut être dans une forme autre que linéaire, à savoir : la forme polynomiale. Nous pourrions nous retrouver dans le cas de figure d'une régression linéaire parfaitement préparée et entrainée dont le score serait mauvais pour la simple et bonne raison que la distribution des données est polynomiale.

C'est un élément qu'il est impossible de savoir à l'avance en tant que data scientist, c'est la raison pour laquelle, l'algorithme doit intégrer des versions polynomiales dont les évaluations seront comparées avec l'évaluation d'une forme linéaire.

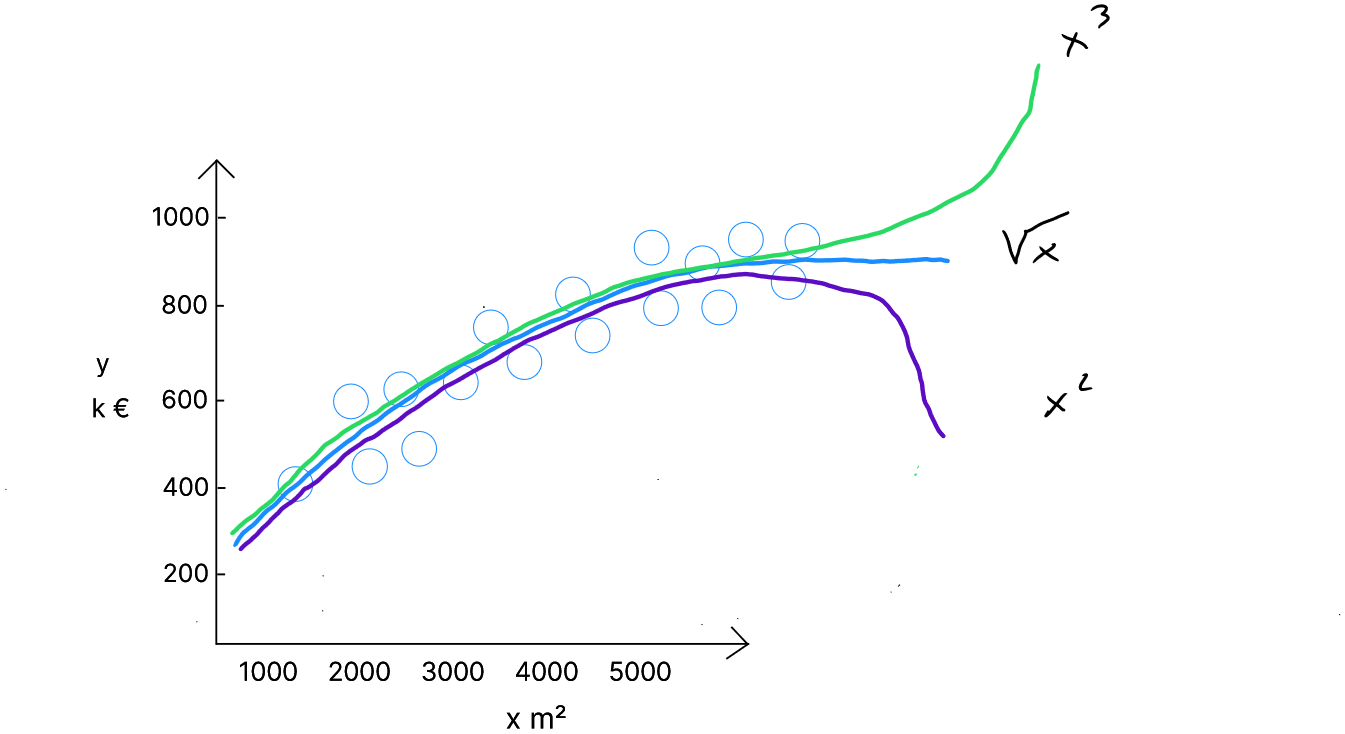
Il s'agit donc de distributions en forme de courbe ( non linéaire ). Dans ce cas, **chaque variable sera répétée et élevée à différentes puissances - jusqu'au degré du polynôme - **.

Régression polynomiale de 2e degré

Prenons l'exemple de la formule d'une régression simple polynomiale de second degrés.

Pour rappel, la formule linéaire correspond à $\hat{y} = b + w * x$.

Si nous souhaitons tester la forme polynomiale de second degré ( ligne mauve dans le graphique ), il nous suffit de dupliquer le prédicteur et le mettre au carré. Ce prédicteur dupliqué et au carré, sera considéré comme un prédicteur à part entière et disposera donc de son propre poids.

Nous retrouvons donc pour la régression simple polynomiale de second degré, la formule suivante :

$$\hat{y} = b + w_1 * x + w_2 * x²$$

Dans le cas d'une régression multiple polynomiale de second degré, chaque prédicteur sera répété et élevé au carré.

Le coefficient w_2 associé à x² contrôle la courbure de la parabole.

Régression polynomiale de 3e degré

Si nous souhaitons tester la forme polynomiale de troisième degré ( ligne verte dans le graphique ), il nous suffit de tripler le prédicteur dont une version est normale, l'autre est au carré et le troisème au cube. Ces prédicteurs supplémentaires ( au carré et au cube ) seront considérés comme des prédicteurs à part entière et disposeront donc de leurs propres poids et les poids associés à leur exposant contrôlent également dans ce cas, la courbure de la parabole.

Régression composite

Il existe également des cas « composite » comme par exemple une régression composite avec terme linéaire et racine carrée ( ligne bleue dans le graphique ). Dans ce cas, nous doublons chaque prédicteur et nous appliquons au duplicat de x, la racine carrée, pour lequel nous obtiendrons également un poids spécifique.

$$\hat{y} = b + w_1 * x + w_2 * sqrt{x}$$

attention

Attention de bien vérifier que nous ne nous retrouvons pas dans le cas d'un surajustement - sur-apprentissage - lors de l'utilisation de modèles polynomiaux à degré élevé dont le risque serait d'obtenir un excellent score en validation et un score médiocre en test ; Par conséquent, une règle non généralisable. Pour éviter le sur-apprentissage, il est recommandé d'utiliser des techniques telles que la validation croisée, la régularisation ou la limitation du degré du polynôme.

Fonction polynomiale en python

from sklearn.preprocessing import PolynomialFeatures


x = data[['x_1', 'x_2', 'x_3', 'x_4', 'x_5', '...', 'x_n']].values  
y = data['y'].values  

poly = PolynomialFeatures(degree=3)

scaler_x = StandardScaler()
scaler_y = StandardScaler()

x_poly = poly.fit_transform(x)

y = scaler_y.fit_transform(y.reshape(-1, 1))
x_poly = scaler_x.fit_transform(x_poly)

x_train, x_test, y_train, y_test = train_test_split(x_poly, y, test_size=0.4, random_state=42)

Régularisation

Comme nous l'avons vu dans la partie sur l'apprentissage supervisé, nous pourrions nous retrouver dans une situation de sous-apprentissage ou sur-apprentissage.

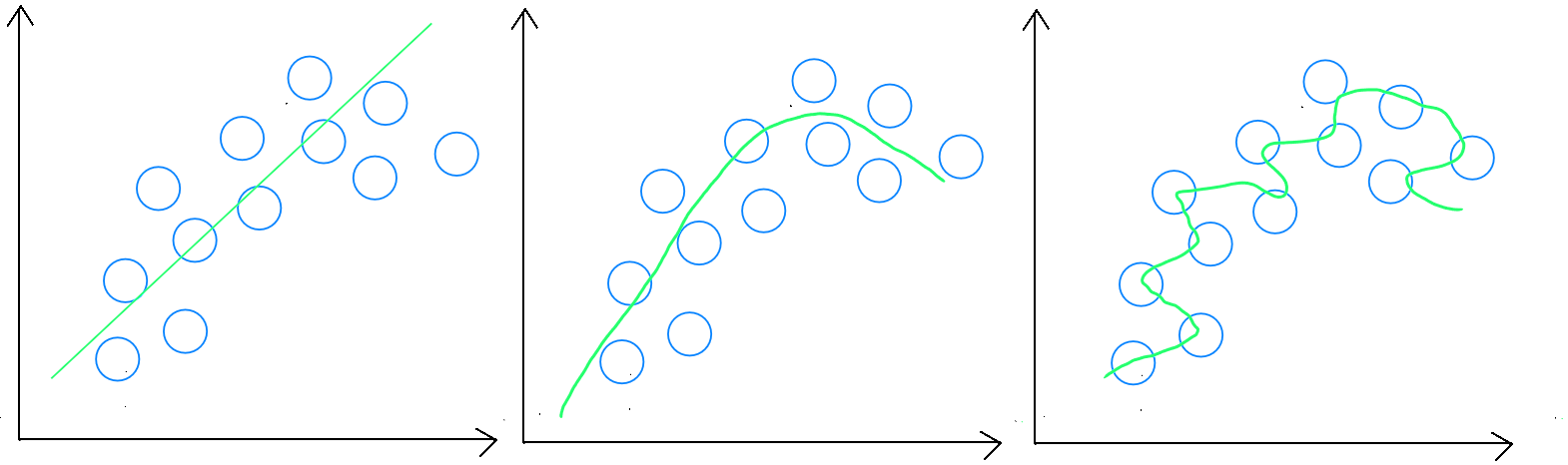
Pour rappel, en sous-apprentissage, l'étape de validation, c'est à dire, l'application du modèle sur les données sur lesquelles il a été entrainé donnera un mauvais résultat. Le modèle n'est pas suffisamment riche pour créer une règle généralisable. Le cas du sous-apprentissage est moins fréquent, et l'option principale à notre disposition en tant que data scientist, est de pouvoir récupérer des variables ou des enregistrements supplémentaires permettant au modèle de mieux identifier les relations.

En sur-apprentissage, il existe plusieurs techniques afin d'éviter que le modèle - très performant dans les données sur base desquelles il a été entrainé - puisse établir une règle généralisable.

La première option est similaire au sous-apprentissage : le modèle ne dispose pas de suffisamment d'enregistrements au regard du nombre de variables utilisées et par conséquent, il a trop « épousé » les données d'entrainement.

La seconde option est l'augmentation ou la réduction des variables. ( Sélection des Variables ). L'augmentation permettra d'assurer un meilleur dispersement des données et donc au modèle de mieux identifier une règle généralisable. Il est toutefois plus habituel de se retrouver dans le cas où le modèle utilise trop de variables et l'objectif est de réduire le nombre de variables via le concept de l'ingénierie des caractéristiques.

Pour la réduction des variables, il existe certaines techniques spécifiques, mais nous pourrions nous retrouver dans le cas où le maintien de l'ensemble des variables est nécessaire et il existe un moyen de palier au sur-apprentissage par l'application de la régularisation.

Prenons l'exemple du cas suivant :

$$\hat{Y} = b + w_1 x_1^{(i)} + w_2 x_2^{(i)} + w_3 x_3^{(i)} + ... + w_p x_p^{(i)}$$

Si pour une raison quelconque, la descente du gradient dans sa recherche de l'optimal local attribuait le poids $w_3$ de la variable $x_3$ à $O$ ; Dans ce cas, les valeurs de la variable $x_3$ seraient annulées par le poids du modèle. Cela correspondrait à supprimer la variable en quelque sorte du modèle.

Le concept de régularisation consiste à réduire l'impact de certaines variables par l'attribution d'un poids plus faible. Concrètement, l'idée est de faire en sorte que l'algorithme d'apprentissage réduise les valeurs des paramètres sans pour autant exiger de mettre des paramètres à $0$. La réduction de certains paramètres permet d'optimiser ce que l'on nomme la régularisation d'apprentissage pour éviter de s'adapter trop aux données d'entrainement. La régularisation s'applique principalement aux valeurs de $w$ même si l'on pourrait également considérer une régularisation sur le paramètre $b$.

La fonction de régularisation peut être appliquée par une modification de la fonction coût. L'idée est d'obtenir des valeurs plus faibles pour les paramètres $w$ dans le but de simplifier le modèle. Le problème est que si l'on dispose de nombreuses variables, il est difficile de distinguer celles qui devraient être pénalisées - davantage responsable du sur-apprentissage - de celles qui devraient être maintenues. C'est la raison pour laquelle dans le principe de régularisation, toutes les variables vont être pénalisées.

Cette pénalisation se fait par l'ajout de la régularisation suivante à la fonction coût :

$$J(w, b) = \min \frac{1}{2m} \sum_{i=1}^n (f(w,b)x^{(i)} - y^{(i)})^2 \textcolor{blue}{\frac{\lambda}{2m} \sum_{j=1}^n w_j^2}$$

il est également possible d'appliquer une régularisation au paramètre $b$ :

$$J(w, b) = \min \frac{1}{2m} \sum_{i=1}^n (f(w,b)x^{(i)} - y^{(i)})^2 \textcolor{blue}{\frac{\lambda}{2m} \sum_{j=1}^n w_j^2} + \textcolor{red}{\frac{\lambda}{2m}b^2}$$

$\lambda$ est le paramètre de régularisation, et comme nous l'avons fait précédemment pour la définition du paramètre alpha $(α)$ de l'algorithme du gradient, c'est nous, en tant que data scientist qui devons définir sa valeur. Le fait de diviser également lambda par $2*m$ sert à adapter la régularisation au reste de la fonction afin de favoriser le choix de la valeur de lambda.

astuce

Gradient descent régularisé (w uniquement)

$J(w, b) = \frac{1}{2m} \sum_{i=1}^n ((w \cdot x^{(i)} + b) - y^{(i)})^2 \textcolor{blue}{\frac{\lambda}{2m} \sum_{j=1}^n w_j^2}$

1. $temp_w = w - \alpha \frac{d}{dw} J(w, b) = w - \alpha \left( \frac{1}{m} \sum_{i=1}^{m} [f_{w,b}(x^{(i)}) - y^{(i)}] x^{(i)} + \textcolor{blue}{\frac{\lambda}{m} w_j}\right)$ ;
2. $temp_b = b - \alpha \frac{d}{db} J(w, b) = b - \alpha \left(\frac{1}{m} \sum_{i=1}^{m} [f_{w,b}(x^{(i)}) - y^{(i)}]\right)$ ;
3. $w = temp_w$ ;
4. $b = temp_b$ ;

Code Python complet

import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import math, copy
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures

data = pd.read_csv('data.csv')
data

x = data[['x_1', 'x_2', 'x_3', 'x_4', 'x_5', '...', 'x_n']].values  
y = data['y'].values  


scaler_x = StandardScaler()
scaler_y = StandardScaler()

x = scaler_x.fit_transform(x)
y = scaler_y.fit_transform(y.reshape(-1, 1))

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4, random_state=42)

#Polynomial 
"""
x = data[['x_1', 'x_2', 'x_3', 'x_4', 'x_5', '...', 'x_n']].values  
y = data['y'].values  

poly = PolynomialFeatures(degree=3)

scaler_x = StandardScaler()
scaler_y = StandardScaler()

x_poly = poly.fit_transform(x)

y = scaler_y.fit_transform(y.reshape(-1, 1))
x_poly = scaler_x.fit_transform(x_poly)

x_train, x_test, y_train, y_test = train_test_split(x_poly, y, test_size=0.4, random_state=42)
"""
#/Polynomial 

def predict(x, w, b):
    p = np.dot(x, w) + b
    return p

def compute_cost(X, y, w, b):
    m = X.shape[0]
    cost = 0.0
    for i in range(m):
        f_wb_i = np.dot(X[i], w) + b           
        cost = cost + (f_wb_i - y[i])**2       
    cost = cost / (2 * m)

    # regularisation L2 (ridge)
    regularization_cost = (lambda_ / (2 * m)) * np.sum(w**2)
    cost += regularization_cost                    
    return cost

def compute_gradient(X, y, w, b,lambda_):
    m,n = X.shape           
    dj_dw = np.zeros((n,))
    dj_db = 0.

    for i in range(m):
        err = (np.dot(X[i], w) + b) - y[i]
        for j in range(n):
            dj_dw[j] = dj_dw[j] + err * X[i, j]
        dj_db = dj_db + err
    dj_dw = dj_dw / m
    dj_db = dj_db / m
    dj_dw += (lambda_ / m) * w

    return dj_db, dj_dw

def gradient_descent(X, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters, lambda_):
    J_history = []
    w = copy.deepcopy(w_in)  
    b = b_in

    for i in range(num_iters):
        dj_db,dj_dw = gradient_function(X, y, w, b, lambda_)  
        w = w - alpha * dj_dw               
        b = b - alpha * dj_db               

        if i<100000:      
            J_history.append( cost_function(X, y, w, b, lambda_))
        
        if i > 1 and abs(J_history[-1] - J_history[-2]) < 0.000001:
            print(f"Early stopping at iteration {i} as cost change is less than 0.000001")
            break 
            
        if i% math.ceil(num_iters / 10) == 0:
            print(f"Iteration {i:4}: Cost {J_history[-1]} ",
                  f"dj_dw: {dj_dw}, dj_db: {dj_db}  ",
                  f"w: {w}, b:{b}")

    return w, b, J_history 

initial_w = np.random.randn(7) 
initial_b =  0    

lambda_ = 0.01
iterations = 10000
alpha = 0.0001 
w_final, b_final, J_hist = gradient_descent(x_train, y_train, initial_w, initial_b,
                                                    compute_cost, compute_gradient,
                                                    alpha, iterations, lambda_)

print(f"(w,b) found by gradient descent: ({w_final},{b_final})")

Évaluation du modèle

Pour l'évaluation du modèle, nous utilisons le RMSE - Root Mean Square Error - évaluation d'un modèle d'estimation

def predict(X, w, b):

    return np.dot(X, w) + b 


def rmse(y_true, y_pred):
    mse = np.mean((y_true - y_pred) ** 2)
    return np.sqrt(mse)

y_pred = predict(x_test, w_final, b_final)

y_pred_original = scaler_y.inverse_transform(y_pred.reshape(-1, 1))
y_test_original = scaler_y.inverse_transform(y_test.reshape(-1, 1))

rmse_value_original = rmse(y_test_original, y_pred_original)

rmse_percentage = (rmse_value_original / np.mean(y_test_original)) * 100

print(f"RMSE on the test set (original scale): {rmse_value_original}")
print(f"RMSE en pourcentage sur l'ensemble de test: {rmse_percentage:.2f}%")

Prédiction sur base de nouvelles valeurs $x$

x_new = np.array([[value_1, value_2, value_3, value_4, value_5, ..., value_n]]) 
x_new_normalized = scaler_x.transform(x_new)
y_new_normalized = np.dot(x_new_normalized, w_final) + b_final
y_new_normalized = y_new_normalized.reshape(-1, 1) 
y_new = scaler_y.inverse_transform(y_new_normalized)
print(f"Predicted value : {y_new[0][0]}")

Polynomial
"""
x_new = np.array([[value_1, value_2, value_3, value_4, value_5, ..., value_n]]) 
x_new_poly = poly.transform(x_new)  # Transformer les nouvelles données pour inclure les termes polynomiaux
x_new_normalized = scaler_x.transform(x_new_poly)
y_new_normalized = np.dot(x_new_normalized, w_final) + b_final
y_new_normalized = y_new_normalized.reshape(-1, 1)
y_new = scaler_y.inverse_transform(y_new_normalized)

print(f"Predicted value : {y_new[0][0]}") 
"""